坐标系的平移与旋转变化

一、坐标系的平移变化

定义

坐标原点发生变化，而坐标轴的方向不发生改变，这样的变化成为坐标系的平移变化。

分析

记平移后的坐标原点为 $O'(h, k)$， 取坐标系上任一点 $P(x, y)$， 利用平面向量，有

即

因此，得到平移后的坐标与原坐标的关系式如下

我们称 (1) 式和 (2) 式为平移公式。

示例

问题

将坐标原点 $O$ 点平移至 $O'(2, -3)$, 求以下各项在新坐标系中的方程。

1. 点 $A(4, 6)$;
2. 直线 $x + 3y = 2$;
3. 曲线 $9 x^2 + 4 y^2 - 36x + 24y - 36 = 0$.

解答

根据平移公式，平移前后的坐标有以下关系

1. 由(2)式，得

   $$\begin{cases} x' = x - 2 = 2 \\ y' = y + 3 = 9 \end{cases}$$

   故平移后的坐标为 $A(2, 9)$

2. 由(1)式，得

   $$(x' + 2) + 3 (y' - 3) = 2$$

   整理得，平移后的直线方程为

   $$x + 3y = 9$$

3. 由(1)式, 得

   $$9(x' + 2)^2 + 4(y' - 3)^2 - 36x' + 24y' -36 = 0$$

   整理得， 平移后的曲线方程为

   $$9 x^2 + 4 y^2 - 36 = 0$$

   即

   $$\dfrac{x^2}{4} + \dfrac{y^2}{9} = 1$$

   可知，该曲线为对称中心在 O'(2, -3) 的椭圆

二、坐标系的旋转变化

定义

保持原点及坐标轴的夹角不变，将两坐标轴绕原点（逆时针）旋转同一角度的变化，称为坐标系的旋转变化。

分析

将坐标系 $Oxy$ 逆时针旋转 θ 得到新坐标系 $Ox'y'$, 则 $x'$, $y'$ 正半轴上的单位向量为

则点 $P(x, y)$ 在新坐标系的坐标即为 $\vec{OP}$ 在两个单位向量上的投影

因此我们可以得到旋转公式

示例

问题

将坐标系 $Oxy$ 旋转 45°, 求以下各项在新坐标系中的方程。

1. 点 $B(6, -1)$;
2. 直线 $x + 3y = 2$;
3. 曲线 $x^2 + y^2 - 6xy + 4= 0$.

解答

根据平移公式，平移前后的坐标有以下关系

1. 由(2)式，得

   $$\begin{cases} x' = \dfrac{\sqrt{2}}{2} x + \dfrac{\sqrt{2}}{2} y = \dfrac{5 \sqrt{2}}{2} \\ y' = -\dfrac{\sqrt{2}}{2} x + \dfrac{\sqrt{2}}{2} y = -\dfrac{7 \sqrt{2}}{2} \end{cases}$$

   故平移后的坐标为 $A(\dfrac{5 \sqrt{2}}{2}, -\dfrac{7 \sqrt{2}}{2})$

2. 由(1)式，得

   $$(\dfrac{\sqrt{2}}{2} x' - \dfrac{\sqrt{2}}{2} y') + 3 (\dfrac{\sqrt{2}}{2} x' + \dfrac{\sqrt{2}}{2} y') = 2$$

   整理得，平移后的直线方程为

   $$2x + y = \sqrt{2}$$

3. 由(1)式, 得

   $$(\dfrac{\sqrt{2}}{2} x' - \dfrac{\sqrt{2}}{2} y')^2 + (\dfrac{\sqrt{2}}{2} x' + \dfrac{\sqrt{2}}{2} y')^2 - 6(\dfrac{\sqrt{2}}{2} x' - \dfrac{\sqrt{2}}{2} y') (\dfrac{\sqrt{2}}{2} x' + \dfrac{\sqrt{2}}{2} y') + 4= 0$$

   整理得， 平移后的曲线方程为

   $$x^2 - 2 y^2 - 2 = 0$$

   即

   $$\dfrac{x^2}{2} - y^2 = 1$$

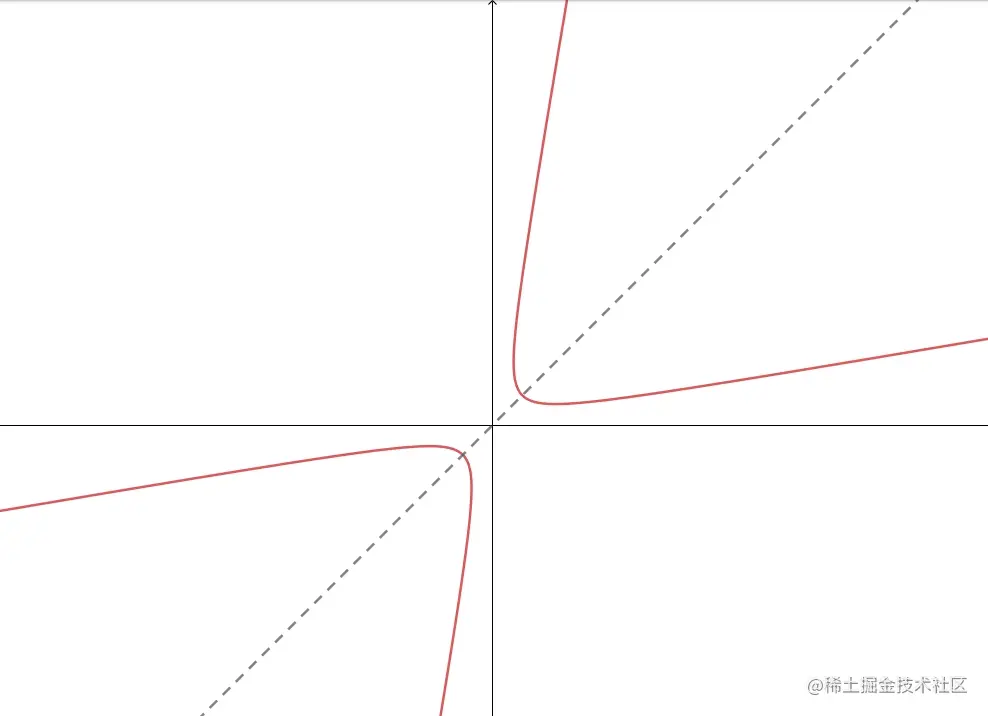
   可知，该曲线为对称轴为直线 $y = x$ 的双曲线