本文已参与「新人创作礼」活动，一起开启掘金创作之路。

4.单层神经网络示例代码

网络结构见图3.1 请点击下面的超链接跳转至github页面：用logistic回归实现一层神经网络用来识别猫的图片其中Logistic_Regression_with_a_Neural_Network_mindset.ipynb文件包含详细的注释和图示，但需要在jupyternotebook中运行；Logistic_Regression_with_a_Neural_Network_mindset.py文件可直接用“python”命令运行，两者的功能是一样的。

5.两层神经网络

5.1.前向传播

\begin{aligned} X&=\left[x^{(1)},x^{(2)},\cdots,x^{(m)}\right]\\ W^{[1]}&=\left[w_1^{[1]},w_2^{[1]},\cdots,w_{n_1}^{[1]}\right]^{T}\\ b^{[1]}&=\left[b_1^{[1]},b_2^{[1]},\cdots,b_{n_1}^{[1]}\right]\\ Z^{[1]}&=W^{[1]}X+b^{[1]}\\ A^{[1]}&=g^{[1]}\left(Z^{[1]}\right)\\ W^{[2]}&=\left[w_1^{[2]},w_2^{[2]},\cdots,w_{n_2}^{[2]}\right]^{T}\\ b^{[2]}&=\left[b_1^{[2]},b_2^{[2]},\cdots,b_{n_2}^{[2]}\right]\\ Z^{[2]}&=W^{[2]}A^{[1]}+b^{[2]}\\ A^{[2]}&=g^{[2]}\left(Z^{[2]}\right)\\ Y&=\left[y^{(1)},y^{(2)},\cdots,y^{(m)}\right]\\ \tag{5-1} \end{aligned}

$(5-1)$ 中从上到下的顺序可以代表前向传播过程。

5.2.反向传播

\begin{aligned} {\rm d}Z^{[2]}&=A^{[2]}-Y\\ {\rm d}W^{[2]}&=\frac{1}{m}{\rm d}Z^{[2]}A^{[1]\ T}\\ {\rm d}b^{[2]}&=\frac{1}{m}np.sum\left({\rm d}Z^{[2]},axis=1,keepdims=True\right)\\ {\rm d}A^{[1]}&={W^{[2]}}^T{\rm d}Z^{[2]}\\ {\rm d}Z^{[1]}&={\rm d}A^{[1]}*{g^{[1]}}'\left(Z^{[1]}\right)\\ {\rm d}W^{[1]}&=\frac{1}{m}{\rm d}Z^{[1]}A^{[0]\ T}\\ {\rm d}b^{[1]}&=\frac{1}{m}np.sum\left({\rm d}Z^{[1]},axis=1,keepdims=True\right)\\ \tag{5-2} \end{aligned}

$(5-2)$ 中从上到下的顺序可以代表前向传播过程。

5.3.关于参数的初始化

在单层神经网络（logistic回归）中，可以将参数初始化wie全零值；但是在多层神经网络中， $W$ 不能初始化为0，否则每一层的各个节点对应的 $W$ 会训练成一样的值； $b$ 可以初始化为0 $W$ 不能初始化为特别大，浅层网络一般是0.01量级；因为太大了的话，激活函数的自变量要么正向很大，要么负向很大，导致斜率趋近于0 ，收敛速度很慢。尤其是你使用 $sigmoid$ 或 $tanh$ 激活函数。如果不使用这些激活函数，但是你是二分类问题（输出层是sigmoid函数），也会出现这个问题.

5.4.2层神经网络示例代码

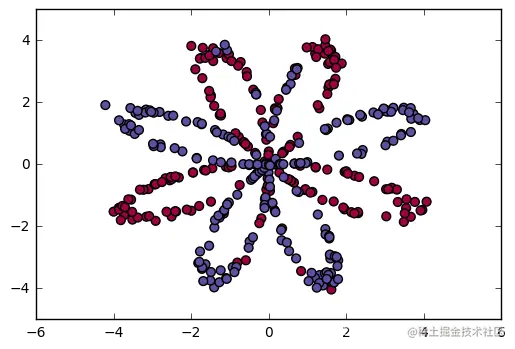
对如下二维平面上的点进行分类：在这里插入图片描述

图5.1 二维平面上的非线性二分类数据集例子

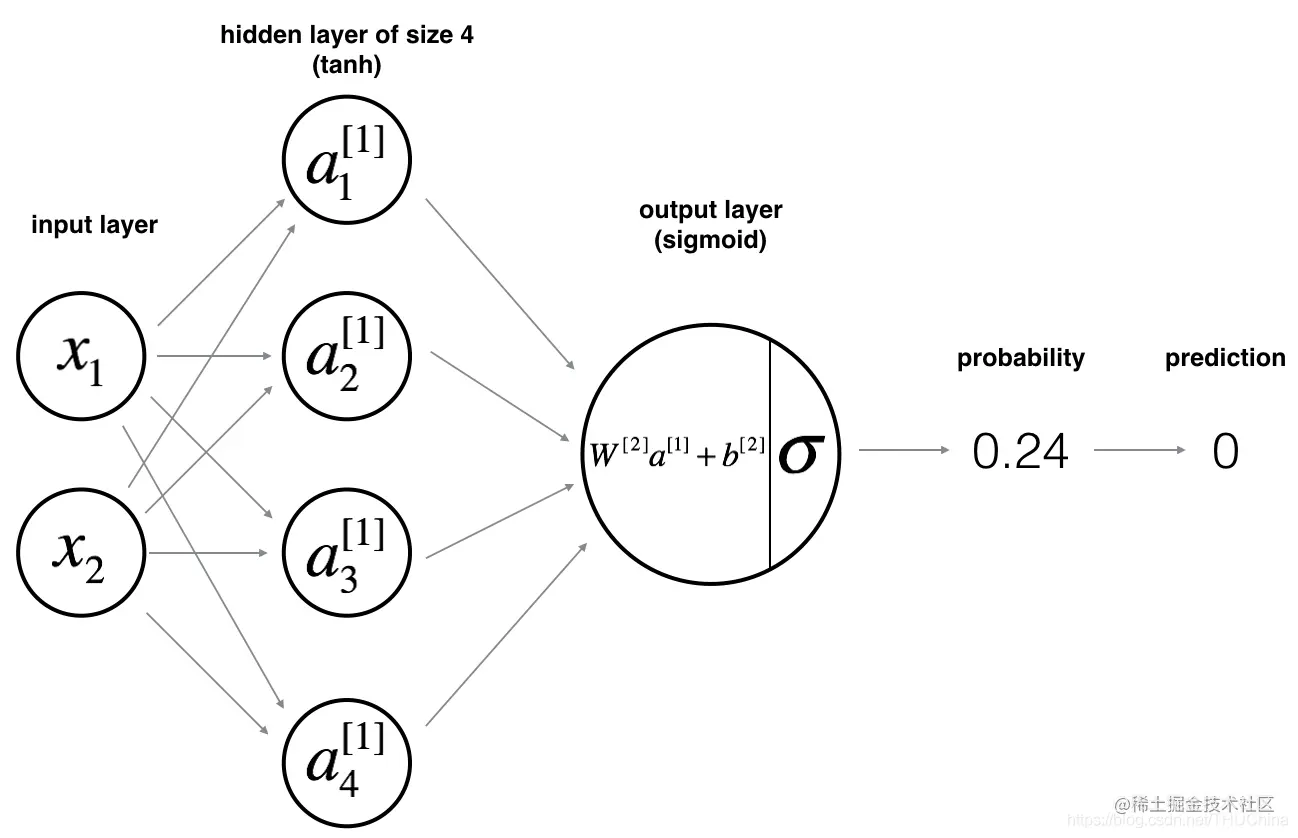
网络结构如下：在这里插入图片描述

图5.2 2层神经网络结构例子

点击下面的超链接查看完整代码： 2层神经网络的示例代码其中Palnar_data_clf_with_one_hidden_layer.ipynb文件包含详细的注释和图示，但需要在jupyternotebook中运行；Palnar_data_clf_with_one_hidden_layer.py文件可直接用“python”命令运行，两者的功能是一样的。

6.深层神经网络

6.1.每层的参数及变量的尺寸

\end{aligned}

6.2.前向传播递推公式

\begin{aligned} X&=\left[x^{(1)},x^{(2)},\cdots,x^{(m)}\right]\\ W^{[l]}&=\left[w_1^{[l]},w_2^{[l]},\cdots,w_{n_l}^{[l]}\right]^{T}\\ b^{[l]}&=\left[b_1^{[l]},b_2^{[l]},\cdots,b_{n_l}^{[l]}\right]\\ Z^{[l]}&=W^{[l]}A^{[l-1]}+b^{[l]}\\ A^{[l]}&=g^{[l]}\left(Z^{[l]}\right)\\ W^{[l+1]}&=\left[w_1^{[l+1]},w_2^{[l+1]},\cdots,w_{n_l+1}^{[l+1]}\right]^{T}\\ b^{[l+1]}&=\left[b_1^{[l+1]},b_2^{[l+1]},\cdots,b_{n_2}^{[l+1]}\right]\\ Z^{[l+1]}&=W^{[l+1]}A^{[l]}+b^{[l+1]}\\ A^{[l+1]}&=g^{[l+1]}\left(Z^{[l+1]}\right)\\ Y&=\left[y^{(1)},y^{(2)},\cdots,y^{(m)}\right]\\ \tag{6-2} \end{aligned}

6.3.反向传播递推公式

\begin{aligned} {\rm d}Z^{[l]}&={\rm d}A^{[l]}*{g^{[l]}}'\left(Z^{[l]}\right)\\ {\rm d}W^{[l]}&=\frac{1}{m}{\rm d}Z^{[l]}A^{[l-1]\ T}\\ {\rm d}b^{[l]}&=\frac{1}{m}np.sum\left({\rm d}Z^{[l]},axis=1,keepdims=True\right)\\ {\rm d}A^{[l-1]}&={W^{[l]}}^T{\rm d}Z^{[l]}\\ \tag{6-3} \end{aligned}

6.4.多层神经网络的示例代码

点击如下超链接。对比了2层神经网络和5层神经网络在对猫分类时的性能 Deep Neural Network - Application.py Deep Neural Network - Application.ipynb

从logistic回归到神经网络——理论与实践（二）