1.logistic回归详解

logistic回归模型是用来解决二分类问题的，因此我们将首先在概率的框架下描述什么是分类问题。分类问题的一般描述如下图所示：在这里插入图片描述

图1.1 分类问题的一般描述

用X代表输入空间，是输入向量的所有可能取值的集合，也叫特征空间；Y代表输出空间，是输出的所有可能取值的集合。 $x^{(i)}\in X$ 代表特征空间的一个样本， $y^{(i)}\in Y$ 代表其类别（标签）。分类问题的一般描述可总结为：利用已知标签的训练集 $X_{train}$ 训练出一个模型，该模型包含一个映射关系 $h:X\rightarrow Y$ ， $h$ 应该能够对新的数据点 $x^{(m+1)}$ 预测其类别 $y^{(m+1)}$ ，并且预测结果应该尽可能好。通常情况下，这种“好”的标准为正确率尽可能高。

以二分类问题为例，用0和1代表可能的类别，也即 $Y=\{0,1\}$ 。我们从概率的框架下来讨论二分类问题：给定输入特征向量 $x$ ，我们希望估计出它分别属于两类的概率 $P(y=0|x;\theta)$ 和 $P(y=1|x;\theta)$ 。因为现在讨论的是二分类问题，可令 $\hat y=P(y=1|x;\theta)$ ，那么只要估计出 $\hat y$ 就可以了。在估计之前，需要选择合适形式的函数对各类别的后验概率建模，一种最简单也是最笨的方法就是令 $\hat y=w ^T x+b$ ，也即线性回归。但是这样可能会导致 $\hat y$ 的值大于1或者大于0，这和概率的定义相违背。因此，我们可以在线性回归的表达式前面加上一层sigmoid函数，也即 $\hat y=\sigma\left(\omega ^T x+b\right)$ 。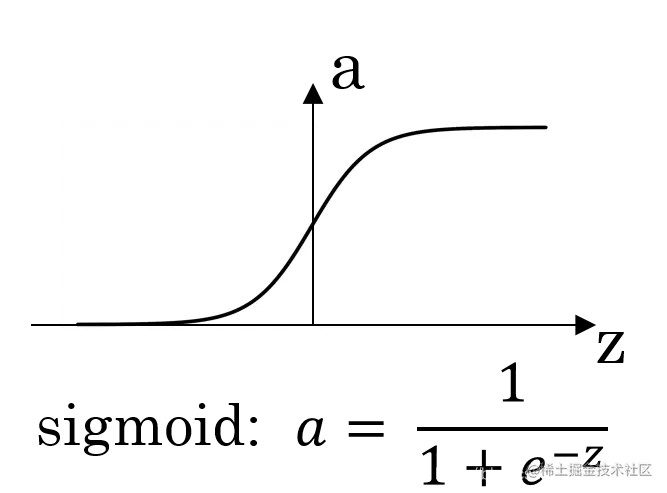sigmoid函数的表达式为： $\sigma (z)=\frac{1}{1+e^{-z}}\\ \tag{1-1}$ 其函数图像为：在这里插入图片描述

到此，我们得到了logistic回归模型： $\hat y=\frac{1}{1+e^{(-\theta^Tx)}} \tag{1-2}$ 注意，在 $(1-2)$ 中，我们将参数项b用 $x_0$ 表示，这样能够写成更紧凑的形式。为了突出参数 $\theta$ ，我们用 $h_\theta$ 表示公式 $(2)$ 中的函数，它代表了在已知特征 $x$ 的情况下，类别为 $y=1$ 的概率，也即 $P(y=1|x;\theta)=h_\theta$ ；显然, $P(y=0|x;\theta)=1-h_\theta$ 假设我们的目标是让分类的错误率最小（即最小错误率决策准则，这是最普遍的一种分类准则）。不难证明，最小化错误等价于最大化各类的后验概率。因此，若 $(1-2)$ 的值大于0.5，则判定为类别1；否则判定为类别0。

注意，logistic模型仍然是一个线性分类模型，因为它的决策面是 $0=w ^T x+b$ ，我一个线性决策面。

2.损失函数的选取

选取好了模型后，接下来要选取损失函数（Loss function），然后在训练集上利用一定的算法（例如梯度下降法）最小化损失函数，从而确定 $h_{\theta}$ 中的参数 $\theta$ 。一种很自然的想法是选取 $L\left(\hat y,y\right)=\frac{1}{2}\left(\hat y-y\right)^2$ 作为损失函数，但是这会导致在后面学习参数的过程中，最优问题不是一个凸问题。我们在这里采用极大似然估计的方法来推导出一个更合理的损失函数，并且该损失函数是凸函数。

2.1.最大化后验概率与极大似然估计

回忆一下极大似然估计的思想：对于可观测的样本 $X$ 及其观测值 $Y$ ，写出该观测值的概率表达式（记为 $L\left(\theta\right)$ )，该概率表达式一般依赖于参数 $\theta$ ，极大似然估计的目标是寻找 $\theta$ 的估计值 $\hat \theta$ 使得 $L\left(\theta\right)$ 最大。对于某一个观测样本 $x^{(i)}$ 和观测值 $y^{(i)}$ ,有：

\begin{aligned} L(\theta)&=P(y^{(i)}|x;\theta)\\ &=(h_\theta(x))^{1\left(y^{(i)}=1\right)}(1-h_\theta(x))^{1\left(y^{(i)}=0\right)}\\ &=(h_\theta(x))^y(1-h_\theta(x))^{1-y}\\ \tag{2-1} \end{aligned}

$L(\theta)$ 也叫似然函数。对数似然函数为：

\begin{aligned} l(\theta) &=\log L(\theta) \\ &=y\log\left(h_\theta(x)\right)+(1-y)\log (1-h_\theta(x)) \tag{2-2} \end{aligned}

$(2-2)$ 就是单个样本的损失函数。下面讨论训练集上的代价函数（cost function）。对于多个观测样本 $X$ 和观测值 $Y$ ，似然函数可写成：

\begin{aligned} L(\theta) &=P(\boldsymbol{Y}|\boldsymbol{X};\theta) \\ &=\prod_{i=1}^{m}P(y^{(i)}|x^{(i)};\theta) \\ &=\prod_{i=1}^{m}(h_\theta(x^{(i)}))^{y^{(i)}}(1-h_\theta(x^{(i)}))^{1-y^{(i)}}\\ \tag{2-3} \end{aligned}

对数似然函数为：

\begin{aligned} l(\theta) &=\log L(\theta) \\ &=\sum_{i=1}^{m}y^{(i)}\log h_\theta(x^{(i)})+(1-y^{(i)})\log (1-h_\theta(x^{(i)}))\\ \tag{2-4} \end{aligned}

因为对数似然函数需要最大化，而损失函数需要最小化，因此我们选择如下表达式作为损失函数：

$(2-5)$ 就是代价函数（cost function），它等价于对所有的 $(2-2)$ 取平均。损失函数（loss function）是定义在单个样本上的，代价函数（cost function）是定义在多个样本上的。

3.梯度下降方法求解最优的参数 $w$ 和 $b$ （一层神经网络）

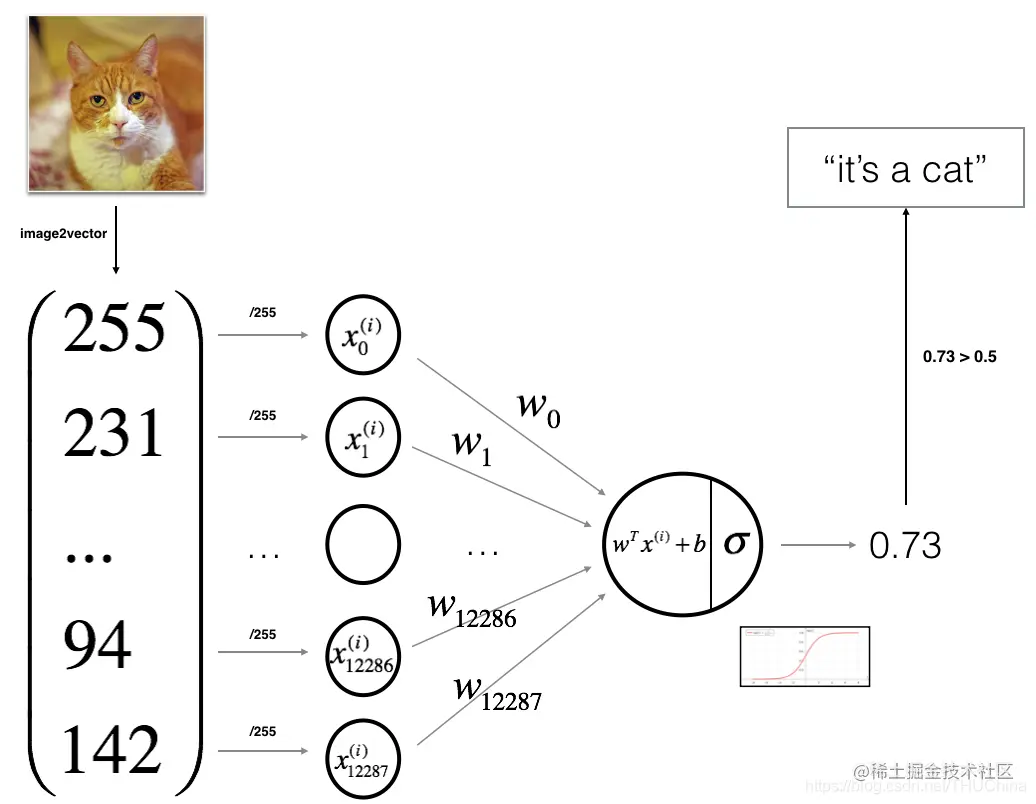
利用logistic可以构造一个只含有输出层的神经网络，其结构图如下：在这里插入图片描述

图3.1 用logistic回归表示的单层神经网络结构图

下面介绍其作为神经网络时的前向传播、反向传播过程，为后面理解更复杂的神经网络打下基础。 logistic回归的代价函数的凸函数，因此可以用梯度下降的方法求得全局最优值，并且与初始化的方式无关，一般利用零初始化。

\begin{aligned} w&:=w-\alpha\frac{\partial J(w,b)}{\partial w}\\ b&:=b-\alpha\frac{\partial J(b,b)}{\partial b}\\ \tag{3-1} \end{aligned}

注意，Andrew NG在Cousera开设的深度学习课程中，求偏导用的是符号 $d$ ，我们这里不区分 $\partial$ 和 $d$ 。下面我们讨论只有输入层和输出层（激活函数为sigmoid函数）的简单神经网络的前向传播和反向传播过程，也即logistic回归。

3.1.前向传播

\begin{aligned} X&=\left[x^{(1)},x^{(2)},\cdots,x^{(m)}\right]\\ Z&=\left[z^{(1)},z^{(2)},\cdots,z^{(m)}\right]\\ &=[w^Tx^{(1)}+b,w^Tx^{(2)}+b,\cdots,w^Tx^{(m)}+b]\\ A&=\left[a^{(1)},a^{(2)},\cdots,a^{(m)}\right]\\ &=\left[\sigma\left(a^{(1)}\right),\sigma\left(a^{(2)}\right),\cdots,\sigma\left(a^{(m)}\right)\right]\\ Y&=\left[y^{(1)},y^{(2)},\cdots,y^{(m)}\right]\\ \tag{3-2} \end{aligned}

$(3-2)$ 中从上到下的顺序可以代表前向传播过程。

3.2.反向传播

先对求导公式进行一些化简：

\begin{aligned} \rm d\it a &= \frac{\rm{d}\it{L(a,y)}}{\rm{d}\it{a}}\\ &= -\frac{y}{a}+\frac{1-y}{1-a}\\ \tag{3-3} \end{aligned}

\begin{aligned} \rm d\it z&= \frac{\rm{d}\it{L(a,y)}}{\rm{d}\it{z}}\\ &= \frac{\rm{d}\it{L(a,y)}}{\rm{d}\it{a}}\cdot \frac{\rm d \it a}{\rm d \it z}\\ &= \left(-\frac{y}{a}+\frac{1-y}{1-a}\right)\cdot a(1-a)\\ &=a-y \\ \tag{3-4} \end{aligned}

有了 $(3-4)$ ，我们就能得到 $\rm{d}\it{Z}=A-Y$ 。因此反向传播过程如下：

\begin{aligned} \rm{d}\it{Z}&=A-Y\\ \rm d\it w&= \frac{1}{m}\cdot X\cdot \rm{d}\it{Z}^T\\ &=\frac{1}{m}X\left(A-Y\right)^T \\ \rm d\it b&= \frac{1}{m}\cdot\sum_{i=1}^{m}\left(\rm{d}\it{Z^{(i)}}\right) \\ \tag{3-5} \end{aligned}

注意， $(3-5)$ 的流程可以理解为先对每一个样本求损失函数关于 $z$ 的梯度，并对每个样本求出 $\rm{d}\it{w}$ ，在对所有样本的 $\rm{d}\it{w}$ 球平均，因此有 $1/m$ 。在这里插入图片描述

图3.2 logistic回归梯度下降

也可以对 $m$ 个样本的代价函数一次性直接求偏导，这需要一定的向量微分和复合函数微分的知识。这样的话，在 $\rm{d}\it{Z}$ 中就会有一个 $1/m$ ，那么在求 $\rm{d}\it{w}$ 时就不用另外再加一个 $1/m$ 了，并且形状可能互为转置，最终的结果是一样的。具体过程这里省略，有兴趣的读者可以自行推导。

参考

Andrew NG Coursera课程《Neural Networks and Deep Learning》有任何问题请联系 languoxing@126.com

从logistic回归到神经网络——理论与实践（一）