用简单的代码和动画解释受自然启发的算法
照片:Sebastian Pena LambarrionUnsplash
在这篇文章中,我们探讨了受自然启发的优化算法--粒子群优化的理论方面,然后将该算法应用于Python中的一个简单例子,用动画GIF表示,以便我们可以看到它是如何工作的。
如果你正在用反向传播的随机梯度下降法训练一个深度学习模型,并且无法摆脱局部最小值,这篇文章可能会帮助你找到另一种方法来解决这个问题。
蜂群是一个代理或有机体的集合;蜂群智能可以定义为蜂群的社会行为,其中自主个体以分散和自组织的方式相互作用。个体的互动提高了对环境的经验知识,使蜂群达到最佳状态。
我们可以在自然界观察到这种智能。例如,众所周知,蚂蚁会找到从它们的蚁穴到食物来源的最短路径。在开始时,个体会探索从目的地出发和到达目的地的各种方向。当发现一条有利的路线时,蚂蚁会用信息素标记这条路,信息素是蚂蚁在地上沉积的化学物质。当更多的蚂蚁走同样的路线时,信息素就会加强,吸引更多的蚂蚁。因此,大多数蚂蚁会跟随并汇聚到最短的路径上。
有一些受自然启发的算法可以模仿蜂群智能。蚁群优化(ACO)源于蚂蚁。人工蜂群(ABC)的灵感来自于蜜蜂在其蜂巢周围的蜂群。这篇文章是关于粒子群优化(PSO),它是由鸟群和鱼群暗示的。
PSO最初是由James Kennedy和Russell Eberhart在1995年提出的。[1] [2] 他们假设,信息的社会共享将为蜂群提供优势。只要资源分布超出预测范围,鱼群中的单个成员就能从其他成员的发现和经验中获利,而不是争夺食物。关键字是 "社会互动"。社会行为增加了个体的适应能力;因此,鱼群中出现了智能。个人的适应能力和集体智慧是相互关联的。
PSO的算法很简单。粒子是搜索空间中的一些简单实体。我们创建一个粒子群,用问题的目标函数来衡量它们的个体适应性。然后,粒子根据其个人最佳位置和虫群迄今为止的最佳位置,从当前位置移动到下一个位置。通过迭代移动,蜂群在几代中逐渐达到目标函数的最佳点。
一些记号。
Number of particles : i
速度调整受三个因素的影响:以前的速度(惯性成分)、单个粒子的最佳位置(认知成分)和蜂群的最佳位置(社会成分)。速度是一个移动的粒子向一个给定方向的速度。粒子的运动在每个方向上都会受到这些权重的影响。系数w被称为惯性权重,它是保持粒子在与前一代相同的方向上运动的力量。c1和c2是恒定的加速度值,其中c1=c2被应用于[1]的原始算法中。这些参数值越高,粒子的运动就越灵敏。我们还假设,在我们的案例中,健身函数是针对最小化问题的。因此,当f(x_i)<f(p_i)时,单个粒子的最佳位置p_i被x_i 所覆盖。
PSO算法如下。
1. Initialise the particle population array x_i
让我们把这个算法翻译成Python代码。为了直观地看到粒子的运动,我们可以将粒子的尺寸简化为两个,即x和y。 脚本是按程序写的。
1.导入图书馆
2.定义健身函数
我们使用函数:f(x,y)=(x-2y+3)^2+(2x+y-8)^2。这个函数的全局最小值是0。所有粒子都应该从随机点向x和y坐标的最佳位置移动,在那里的值变得接近0。
3.更新速度
我们应用r1,r2 和w的随机值。c1和c2被赋予较小的值,为0.1。惯性值可以安排;从0.9开始,逐渐减少到0.4。在我们的案例中,我们按照[3]的实验,生成最小为0.5、最大为1的正态分布,并在每一代中随机选择一个值。
4.更新位置
如算法中所述,新位置是当前位置和速度的总和。
5.PSO的主要功能
首先,我们初始化粒子,它们的最佳位置、速度和健身值。我们还根据粒子的初始位置设置全局最佳位置。然后,我们从一个世代循环到另一个世代。当算法达到最大代数或成功标准时,应该停止。在我们的案例中,它是当平均健身值超过一个特定值时。
6.设置参数值并运行算法
population = 100
我们创建了100个粒子,其中的位置被随机放在x和y坐标上,范围在-100和100之间。由于函数取的是x和y,粒子的位置是二维的。成功标准是0.001或更低。如果满足该标准,程序应在第400代之前停止。
通过以上述配置运行该算法,我们得到了以下结果。
Global Best Position: [2.60008033 2.799968 ]
由于其随机性,每次运行程序时,结果都会发生变化。花了68代才达到成功标准。最好的粒子到达了x≈2.6和y≈2.8的位置*,*健身函数返回全局最小值。
与其把结果写成文字,不如让我们直观地看到粒子的运动,这样会更有见地。
7.Matplotlib绘图和动画
画出函数的线框有助于看到哪里是全局最小值。每一代的图像都应该被捕获。下面是同一个例子的输出。
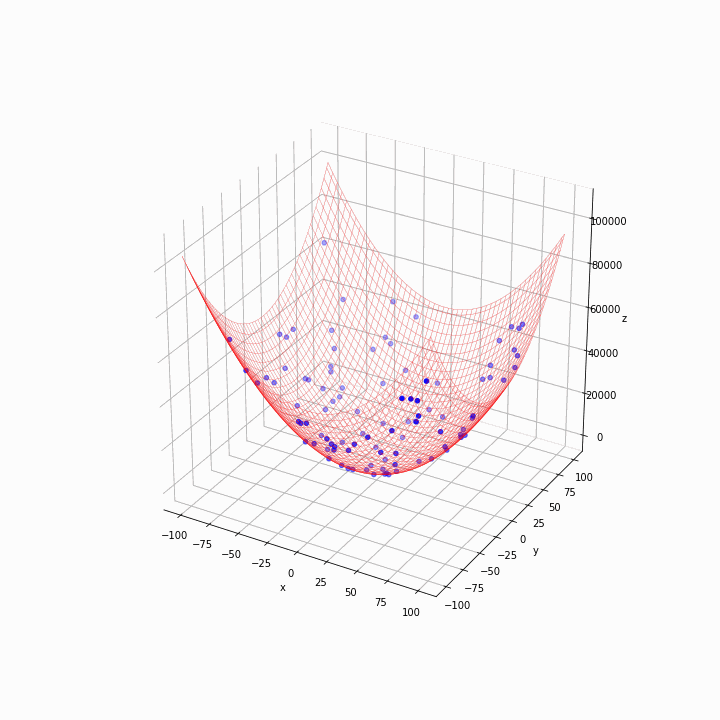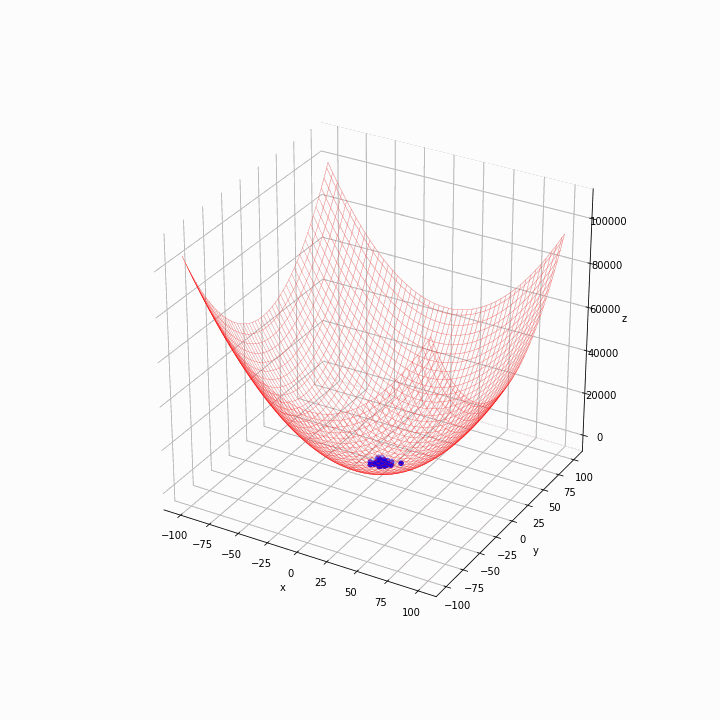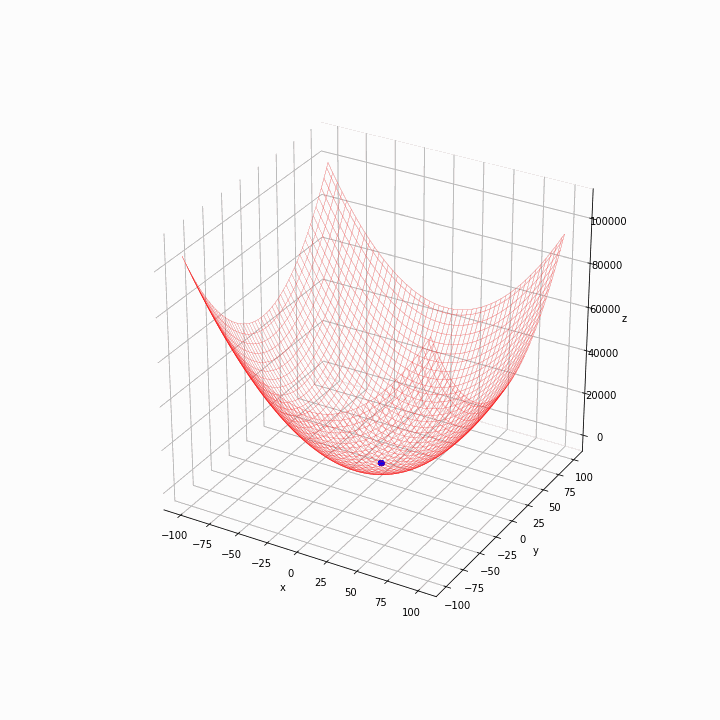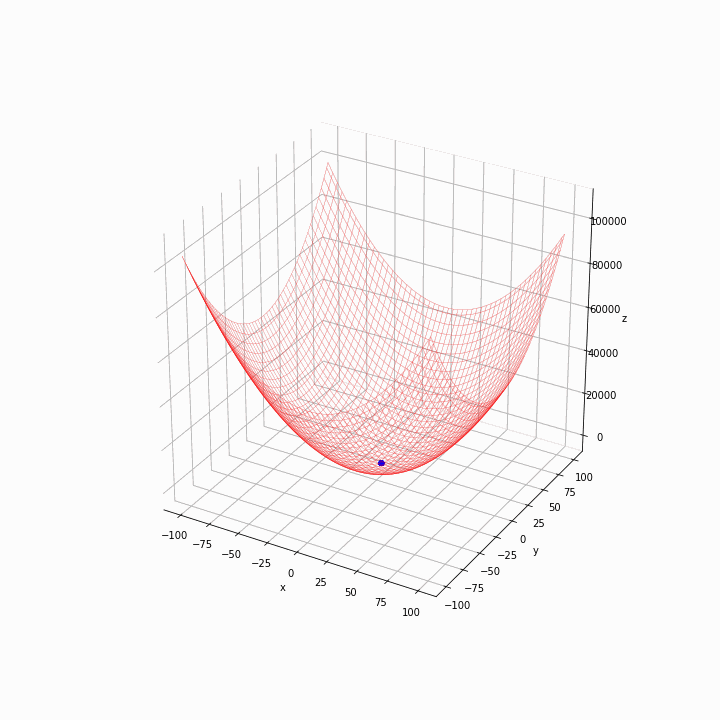
动画粒子在各代中的运动。作者的照片。
在第一代中,粒子是分散的。他们迅速向网格底部移动,看起来算法正在按预期工作。我们可以通过改变健身函数和超参数,如惯性权重w以及认知和社会系数*(c1和c2*)来优化算法,做一些更多的实验。
像PSO这样的群集智能是一类元启发式算法,被认为可以在合理的计算时间内为复杂的优化问题找到一个接近最优的解决方案。如果我们应用该算法来训练一个神经网络,它就特别有用。它的好处是双重的:全局搜索和并行化。
我们可以将每个粒子转化为一个n维数组,代表神经元之间的权重。正如我们在GIF动画中看到的,每个粒子在不同的方向上做运动。与在本地搜索最佳点的反向传播学习算法不同,PSO使得同时探索许多不同的权重参数集成为可能,从而有助于避免通往局部最小值的路径。此外,健身函数与网络拓扑结构无关;评估每个粒子健身的计算可以并行化。
这篇文章用一个简单的代码探讨了粒子群优化算法,以了解其机制。如果你觉得PSO在ML上的应用很有趣,我强烈建议你看看下面这篇文章,关于机器学习与各种元启发式算法的结合。
参考文献。
[1] J. Kennedy and R. Eberhart, "Particle swarm optimization," Proceedings of ICNN'95 - International Conference on Neural Networks.
[2] Poli, R., Kennedy, J. & Blackwell, T. Particle swarm optimization.Swarm Intell 1, 33-57 (2007).https://doi.
org/10.1007/s11721-007-0002-0[3] R. Eberhart and Yuhui Shi, "Particle swarm optimization:发展、应用和资源",2001年进化计算大会论文集(IEEE Cat. №01TH8546),2002年8月。
Swarm Intelligence:粒子群优化在Python中的编码和可视化》最初发表在《走向数据科学》杂志上,人们通过强调和回应这个故事继续对话。