在这篇文章中，我们解释了如何使用除法和征服的方法，用理论上最少的比较次数找到数组中的最小和最大元素。

让我们来理解这个问题

给定一个大小为'n'的数组a[]，我们需要用最小的比较法找到数组中最小和最大的元素。

For example:

Let 
Input array elements:

a[] = {10, 8, 9, 20, 5, 15, 3, 12}


Output:

Maximum element in the array is 20
Minimum element in the array is 3

解决问题的方法

使用循环的强制方法。
使用分割和征服的方法。

方法一：蛮力法

算法

开始max-min
有数组'a'，数组'n'的大小，和一个指针 "minmax "作为输入参数。
声明变量max和min，并将a[0]初始化为两者，即。

int max = a[0]
int min = a[0]

现在我们将开始一个循环，从1到(n-1)第1个索引遍历数组'a'，并将每个元素与max和min做比较。

for i = 1 to (n-1)

条件-1：如果(a[i]>max)，那么max=a[i]，如果第i个索引的值大于max，那么把max=a[i]。

    if a[i] > max
        max = a[i]

条件-2：如果（a[i] < min），那么min = a[i]，意思是如果第i个索引上的值小于min，那么把min = a[i]。

    else
        if a[i] < min 
            min = a[i]

for-loop结束。
现在我们可以把两个值（最大值和最小值）存储到minmax[]数组中，从而返回它们。

minmax[0] = max
minmax[1] = min

结束max-min。

代码

#include<bits/stdc++.h>
using namespace std;

/*-----------Min-Max Function-------------*/
void max_min(int a[], int n, int *minmax){
    int max = a[0];
    int min = a[0];
    for(int i = 1; i < n; i++){
        if(a[i] > max)
            max = a[i];
        else
        if(a[i] < min)
            min = a[i];
    }
    minmax[0] = max;    
    minmax[1] = min;
}

/*-------------Driver Function-------------*/
int main(){
    int a[] = {11, 9, 20, 21, 0, 15, 4, 13};    //Taking array 'a'
    int minmax[2] = {0};    //Taking an extra array minmax to store max & min values
    max_min(a, 8, minmax);  //calling function max_min()
    cout<<"\n Maximum element in the array is "<<minmax[0];  //Printing max value
    cout<<"\n Minimum element in the array is "<<minmax[1];  //Printing min value
    return 0;
}

输出。


 Maximum element in the array is 21
 Minimum element in the array is 0

复杂度

时间复杂度。O(n)，由于循环，
空间复杂性。O(1),由于数组的原因，是常数

最小的比较数是(n-1)个比较数。比如说。数组中的元素按升序排列

a[] = {2, 4, 6, 10, 20, 25}

Output:
Maximum element in the array is 25
Minimum element in the array is 2

问题

需要的最大元素比较数

((2*n)-2)

((2*n)-1)

(n-1)

(2*n)

采取最坏情况的数组（降序数组），其中每个元素的if-else条件都在运行。

方法-2：分而治之

算法

在这种方法中，我们将使用递归树法。
开始max-min
函数有一个数组'a'，开始索引's'，结束索引'e'，min，max作为输入参数。
条件一：如果数组中只有一个元素。那么max = a[s]，min = a[s]，并返回值。

if(s == e)
    max = a[0]
    min = a[0]

条件2：如果数组中只有两个元素。那么两个元素中较大的元素将被分配到max，较小的元素将被分配到min，也就是说。

if(s == e-1)
    if(a[s] < a[e])
        max = a[e]
        min = a[s]
    else
        max = a[s]
        min = a[e]

条件3：取3个变量，例如mid，max1，min1，并将它们分配如下。

mid = (s + e)/2
min1 = INT_MAX
max1 = INT_MIN

现在我们将以递归的方式调用max-min，并在这个过程中相应地改变max和min的值，
即

。

max_min(a, s, mid, min, max)

这里我们以递归树的方式给出数组的前一半。

max_min(a, mid+1, e, min1, max1)

现在我们
将比较max和max1，min和min1，如果需要的话改变max和min。

if(max1 > max)
    max = max1
if(min1 < min)
    min = min1

结束 max-min

代码

#include<bits/stdc++.h>
using namespace std;


/*-----------Min-Max Function-------------*/
void max_min(int a[], int s, int e, int *min, int *max){
   //condition-1
   if(s == e){
    *max = a[s];
    *min = a[s];
   }
   //end condition-1
   
   else
   //condition-2
   if(s == e-1){
       if(a[s] < a[e]){
           *max = a[e];
           *min = a[s];
       }
       else{
           *max = a[s];
           *min = a[e];
       }
   }
   //end condition-2
   
   //condition-3
   else{
       //Divide
       int mid, max1, min1;
       max1 = INT_MIN;
       min1 = INT_MAX;
       mid = (s + e)/2;
       max_min(a, s, mid, min, max);
       max_min(a, mid+1, e, &min1, &max1);
       //Conquer
       if(max1 > *max)
            *max = max1;
       if(min1 < *min)
            *min = min1;
   }
   //end condition-3
   
}

/*-------------Driver Function-------------*/
int main(){
    int a[] = {11, 9, 10, 25, 8, 15, 4, 13, 2};    //Taking array 'a'
    int max, min;   //taking max and min elements
    max = min = a[0];
    max_min(a, 0, 8, &min, &max);  //calling function max_min()
    cout<<"\n Maximum element in the array is "<<max;  //Printing max value
    cout<<"\n Minimum element in the array is "<<min;  //Printing min value
    return 0;
}

输出。

 Maximum element in the array is 25
 Minimum element in the array is 2

复杂度

时间复杂度。O(n)
空间复杂度。O(log(n))，由于递归树(堆栈)的存在

比较次数：
条件1：零比较，如果n=1
条件2：一个比较，如果n=2
条件3：*2T(n/2)+2比较，如果n>2
总比较次数：(((3n
*

)/2)-2) {如果'n'是2的幂}。

Tree

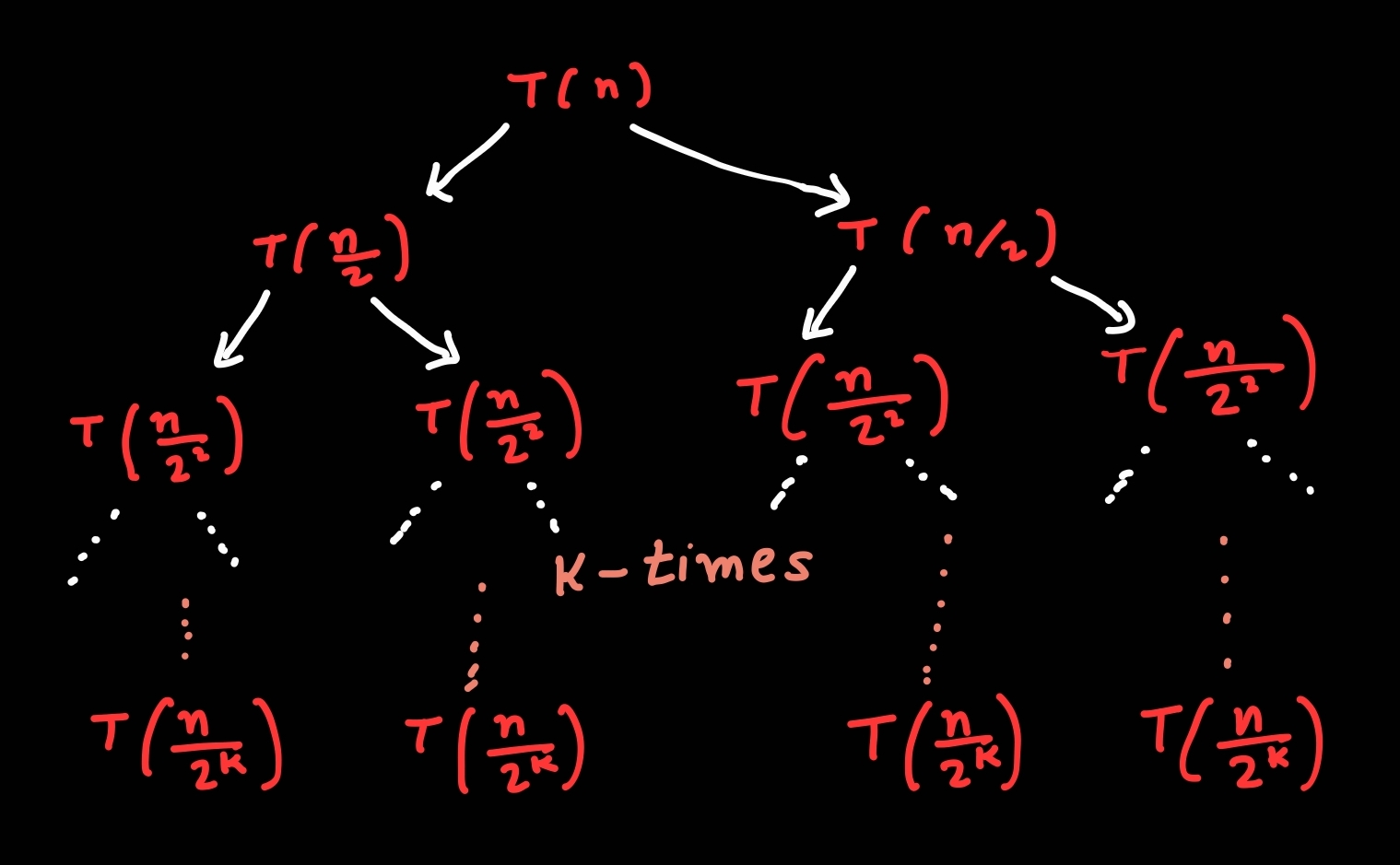
T(n) = 2*T(n/2) + 2
T(n) = 2*[2*T(n/(2^2)) + 2] + 2
T(n) = (2^2)*T(n/(2^2)) + (2^2) + 2
... k-times
T(n) = (2^k)*T(n/(2^k)) + (2^k) + ... + (2^2) + 2
T(n) = (2^k)*T(n/(2^k)) + 2*[(2^k)-1]
put n/(2^k) = 2
T(n) = (n/2)*T(2) + 2*[(n/2)-1]
according to above condition-2, T(2) = 1
T(n) = (n/2) + 2*[(n/2)-1]
T(n) = {[(3*n)/2]-2}

结论

蛮力

时间复杂度。O(n)
空间复杂度。O(1)

分割和征服

时间复杂度。O(n)
空间复杂度。O(log(n))

分割和征服中的比较次数比蛮力少。
- 蛮力：最小->(n-1)个比较，
  最大->((2*n)-2)个比较。
- 分割和征服：(((3*n)/2)-2)对所有情况进行比较。

问题

在有n个不同元素的数组中，找到一个既不是最小也不是最大的元素的时间复杂度是多少？

O(1)

O(n^2)

O(n)

O(logn)

通过OpenGenus的这篇文章，你一定对寻找数组中的最小和最大元素有了完整的认识。

阵列中的最小和最大元素

目录