本文已参与「新人创作礼」活动，一起开启掘金创作之路。

随机变量的数字特征——《概率论及其数理统计》第四章学习笔记

本来这章应该早点弄出来的，但是奈何我太太太能摆了，所以一直没弄。这次快点弄出来吧。

参考教材不变，依旧是 盛骤 浙大第四版的 《概率论与数理统计》。

这次的内容其实就是四个知识点，数学期望、方差、协方差、协方差矩阵。其中后两个知识点我尽力写好。

MindMap

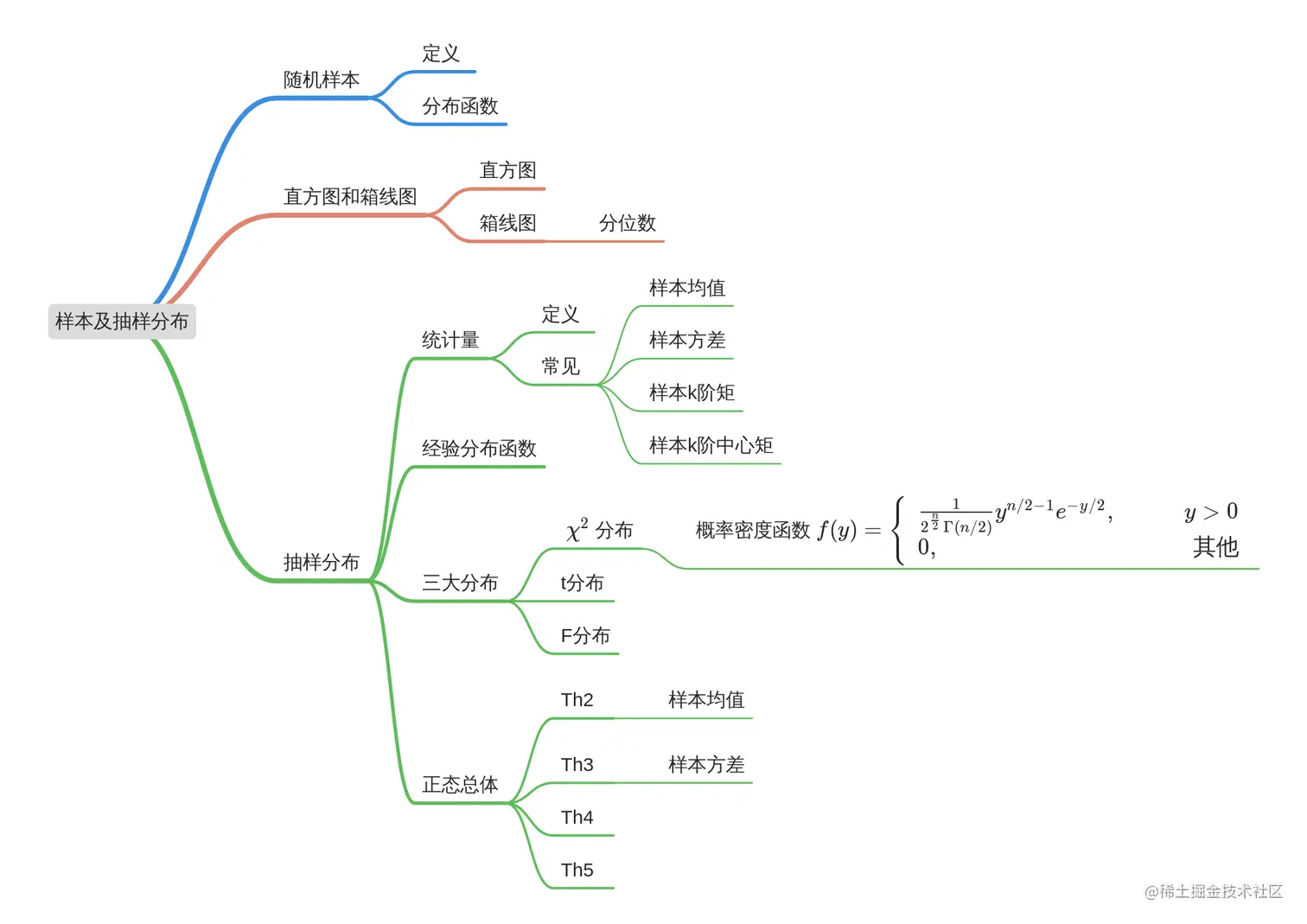
先来看期望吧。

数学期望

定义

数学期望其实很好理解，就是均值，当然这里并不是直接计算样本的均值，而是要考虑到样本对应的概率。我们分离散和连续两类来讨论数学期望。

离散型

对随机变量X的分布律为 $P\{X=x_k\} = p_k, \quad k = 1, 2...$

若级数$\sum_{k=1}^\infty x_k p_k$

绝对收敛，则称改级数为X的 数学期望 ，记为E(X)。即$E(X) = \sum_{k=1}^\infty x_kp_k$

连续型

当我们把上面的求和换成积分就得到了连续型的数学期望$E(X) = \int_{-\infty}^{\infty}{xf(x)}dx$

函数期望的两个定理

设Y 是随机变量 X 的函数，Y=g(X) (g 是 连续 函数)

0. 如果X 是离散型，其分布律为 P{X =xk} = pk，k=1，2，...，若对应的无穷级数 绝对收敛 则有$E(Y) = E[g(X)] = \sum_{k=1}^\infty {g(x_k)p_k}$
1. 如果X是 连续型，其 概率密度为 f(x)，若对应积分绝对收敛，则$E(Y) =E[g(X)] = \int_{-\infty}^{\infty}{g(x)f(x)dx}$

根据上面两个定理我们可以轻松地解决函数类型的数学期望问题。

性质

关于数学期望有以下4个非常重要的性质：

0. C 是 常数， E(C) = C.

1. X 是一个随机变量，C是常数，则$E(CX) = CE(X)$

2. X，Y是两个随机变量，则$E(X+Y) = E(X) + E(Y)$

   该性质可以推广到多个随机变量加和的情况。

3. X，Y 互相独立，则$E(XY) = E(X)E(Y).$

   和3类似，也可以推广到多个随机变量乘积的情况。

方差

方差 我们可以直观地理解为表示数据的 偏离程度，或者说数据的 集中程度。

定义

设X是一个随机变量，若 E{ [X - E(X)] ^ 2} 存在，则称 该式为 X 的 方差，记为 D(X) 或 Var(X)，即$D(X) = Var(X) = E\{[X - E(X)]^2\}$

它的开平方，我们记为$\sigma(X)$

称为 均方差 或 标准差。

离散型

$D(X) = \sum _{k=1}^\infty {[x_k - E(X)]^2p_k}$

连续型

$D(X) = \int _{-\infty}^{\infty} {[x-E(X)]^2f(x)dx}$

除了用定义，我们还可以使用下列式子来计算方差：

$D(X) = E(X^2) - [E(X)]^2$

tips：变量标准化

其实这个技巧在第二章的正态分布的例题中，其实我们也有接触过，具体如下 $E(X)=\mu, \quad D(X)= \sigma \\ 取 X* = \frac{X-\mu}{\sigma} \\ E(X^*) = 0, \quad D(X^*) = 1$

X* 就是 X 的 标准化变量。

四个重要性质

在随机变量的 方差存在 的情况下，有如下性质：

0. C是常数， D(C) = 0.

1. X 是随机变量，C 是常数，有$D(CX) = C^2D(X), \quad D(X + C) = D(X).$

2. D(X + Y) = D(X) + D(Y) + 2E {(X-E(X)(Y-E(Y))) }若 X，Y 互相独立，则有$D(X+Y) = D(X) + D(Y).$

   一样，也是可以推广多个变量。

3. D(X) = 0 的 充要条件 是 X 以概率 1 取常数 E(X), 即 $P \{X=E(X) \} = 1$

切比雪夫不等式

设 X 的 E(X) = μ， D(X) = σ^2

协方差及相关系数

对于二维随机变量，我们除了可以讨论它的 期望 和 方差，我们还可以讨论这两个随机变量间的关系。

协方差和相关系数其实我们在 数据分析 的时候，其实是经常使用的两个数据性质。我们先看课本上对于 这两个量的定义。

定义

$\forall \epsilon > 0 \\ P\{|X - \mu | \geq \epsilon \}\leq \frac{\sigma^2}{\epsilon^2}$

协方差

记为 Cov(X, Y) , $Cov(X, Y) = E \{[E-E(X)][Y-E(Y)] \}.$

相关系数

$\rho_{XY} = \frac{Cov(X,Y)}{\sqrt{D(X)D(Y)}}$

根据定义，可以很容易就知道$Cov(X,Y) = Cov(Y,X), \quad Cov(X, X) = D(X)$

对于任意两个随机变量，存在如下等式$D(X+Y) = D(X) + D(Y) + 2Cov(X,Y).$

我们将 协方差的式子展开，其实就可以得到我们经常用来 计算 的式子$Cov(X, Y) = E(X,Y) - E(X)E(Y).$

协方差性质

0. 数乘性质$Cov(aX, bY) = abCov(X,Y), \quad a,b 是常数$

1. 分配$Cov(X_1 + X_2, Y) = Cov(X_1, Y) + Cov(X_2, Y)$

相关系数的两个定理

0.$|\rho_{XY}| \leq 1$ 0. 相关系数为1的充要条件是 存在常数 a，b使得$P\{Y = a+bX\} = 1$

不相关与独立

这两个是一个集合的包含问题，或者说是不相关是 独立 的 必要条件， 而独立 则是 不相关 的 充分条件。

对于不相关，我们可以用 相关系数 = 0，或者协方差为0 来证明。

而对于变量独立，我们则需要按照定义来证明。

矩、协方差矩阵

只能说我线性代数没学好，现在看这一节有点小懵逼。

设(X, Y) 是 二维随机变量，有如下定义

定义

矩

0. 若$E(X^k), \quad k = 1, 2,...$

   存在，则称其为 X 的 k阶原点矩， 简称k阶矩。

1. 若$E\{[X-E(X)]^k \}, \quad k = 2, 3,...$

   存在，称其为 X 的k阶中心矩。

2. 若$E(X^kY^l), \quad k,l = 1, 2,...$

   存在，称其为 X 和 Y 的 k+l 阶混合矩

3. 若$E\{[X-E(X)]^k[Y-E(Y)]^l \}, \quad k,l = 1,2,...$

   存在，称它为 X 和 Y 的 k+l 阶混和中心矩。

显然 原点矩其实就是 期望，中心矩 其实就是 方差， 协方差 就是 混合中心距。

协方差矩阵

我们对二维随机变量(X1, X2) 有四个二阶中心矩（假设都存在），记为下式

$c_{11} = E\{[X_1 - E(X_1)]^2 \}, \\ C_{12} = E\{[X_1 - E(X_1)][X_2-E(X_2)] \} = c_{21} \\ C_{22} = E\{[X_2 - E(X_2)]^2 \}$ 排成矩阵就是

c11, c12

c21, c22

该矩阵就是 (X1， X2) 的 协方差矩阵。值得注意的是，协方差矩阵也是一个对称阵。

四条重要性质

关于n维正态随机变量有如下性质：

0. 每一个分量 Xi， 都是正态随机变量，反之，则可以证明n维正态随机变量。

1. 服从n维正态分布的充要条件是 $\sum_{i= 1}^{n} {l_iX_i}, \qquad \exist l_i \neq 0$

   服从一维正态分布。

2. 设 Yi 是 Xi 的线性函数，则对应的 Yi 组成的 n 维随机变量也服从n维正态分布。该性质又称为 线性变换不变性。

3. 若 n维随机变量服从 n维正态分布，则随机变量相互独立和随机变量两两不相关等价。

后话

这一章整体来说比较难一点，大家不妨可以把例题还有习题都做一下（emmm，虽然我自己没做完）。