持续创作,加速成长!这是我参与「掘金日新计划 · 6 月更文挑战」的第 2 天,点击查看活动详情。
- 原文地址:Demystifying the 0-1 Knapsack Problem
- 原文作者:The Educative Team
- 译文出自:掘金翻译计划
- 本文永久链接:github.com/xitu/gold-m…
- 译者:Usualminds、jaredliw
- 校对者:Lokfar、DylanXie123
在所有与动态规划有关的面试里,你非常有可能会被问到背包问题。背包问题常常让面试者感到焦虑,因为它不仅解决方案复杂,而且问题变种也多。
为了能让你熟悉多种语言下的背包问题,今天,我们将探讨两种流行的解决方法:递归法和自顶向下的动态规划法。读完本文以后,希望你能充满自信地求解此类问题。
重点内容
- 什么是背包问题?
- 暴力递归法
- 使用动态规划后的解法
- 接下来要学什么?
什么是背包问题?
背包问题是计算机科学中最热门的动态规划面试题之一。
问题描述如下:
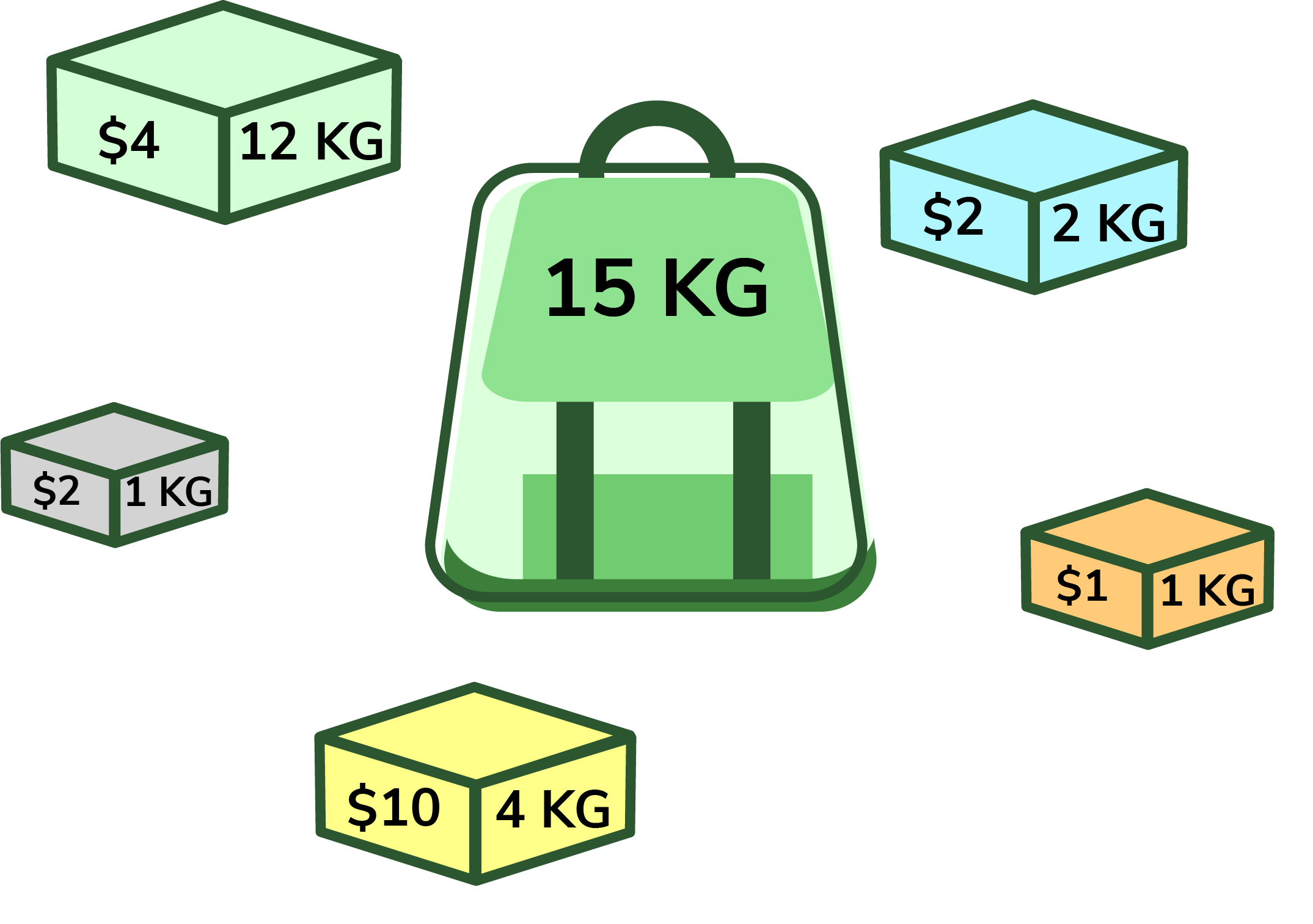
假设你是一个带着背包的小偷,你的背包可以容纳的总重量为 capacity。此时,你有 n 个不同的物品,每个物品都有固定的重量和价值,重量和价值以整数数组表示。创建一个函数 knapsack(),找到最佳的物品选择方案,使得所选物品的总价值最大,同时总重量不超过背包总容量 capacity。
背包问题变种
背包问题有两个主要的变种:部分背包问题和 0-1 背包问题。部分背包问题允许你分割物品来使背包内物品价值最大化,而 0-1 变种则不允许分割物品 —— 对于每件物品,你只能选或者不选。
另一个常见的变种是带约束条件的背包问题,它对物品个数进行了限制,使得你不能选择重复选择某一种物品。对于每一种物品,程序必须决定将它放在包中或者抛弃它。
在高级别的面试中,体积会作为另一个约束属性。对于这种变种,每个物品都有一个固定的体积,背包也有一个体积限制。
背包问题考察哪些技能?
这个问题之所以受欢迎,是因为它一次性考察了很多所需的技能,并且其变种也时常能让面试者措手不及。换句话说,你必须真正理解问题和代码的逻辑,单纯只靠记忆不会让你走得太远。
不论是哪种变种,背包问题的最优解始终都是动态规划解。面试官可以用这个问题来考察你的动态规划能力,同时确定你是否能得出问题的最优解。
背包问题的另一个常见的解法是使用递归。如果面试官重视这两项技能,他可能会要求你同时提供这两种解法。这是一个很常见的要求,因为面试官可以从中了解你如何从递归解转变为动态规划解。
背包问题也测试你组合优化问题的处理方式。这在工作中有许多实际的应用,因为所有的组合优化问题都是寻求在约束条件下的最大收益。
例如,组合优化用于解决以下问题:
- 确保在资源有限的云系统上运行的程序最佳
- 优化固定管网的供水
- 自动计划最佳包裹运送路线
- 优化公司的供应链
在应聘管理或创建自动优化软件的相关岗位时,你多半会遇到背包问题。
暴力递归法
这个问题最直观的解法是暴力递归。这个解法之所以暴力,是因为它计算所有可能子集的总重量和价值,然后选择在最大容量限制之下的具有最高价值的子集。
虽然这是一个有效的解法,但它不是最优解,因为其时间复杂度是指数级的。如果要求使用递归,请使用此解法。这也可以作为后续动态规划解的一个很好的起点。
时间复杂度:O(2^n),因为有大量重复的子调用
空间复杂度:O(1),不需要额外的存储空间
解决方案
以下是算法的可视化表示。
备注:图中所有红色的集合都超出了我们背包的容量,而浅绿色的集合在容量范围内,但不是最大值。
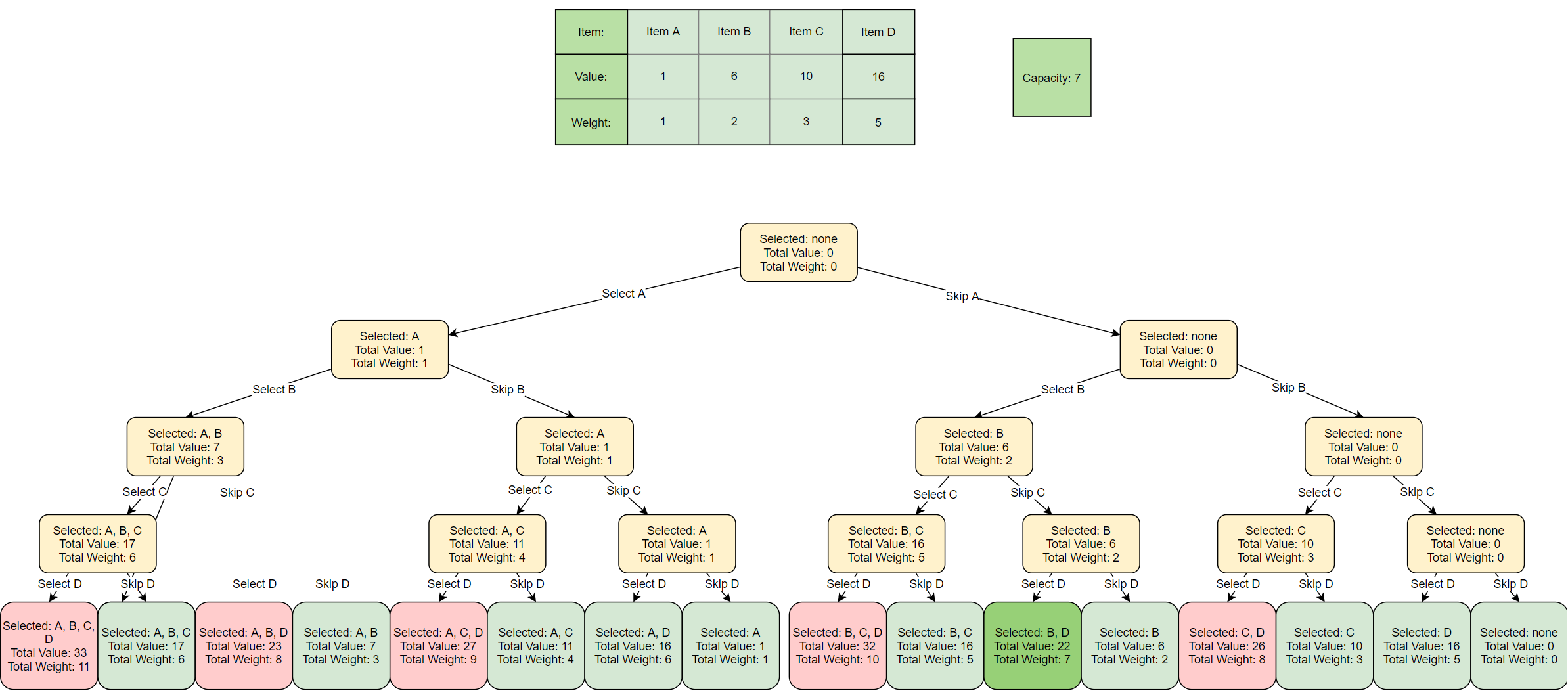
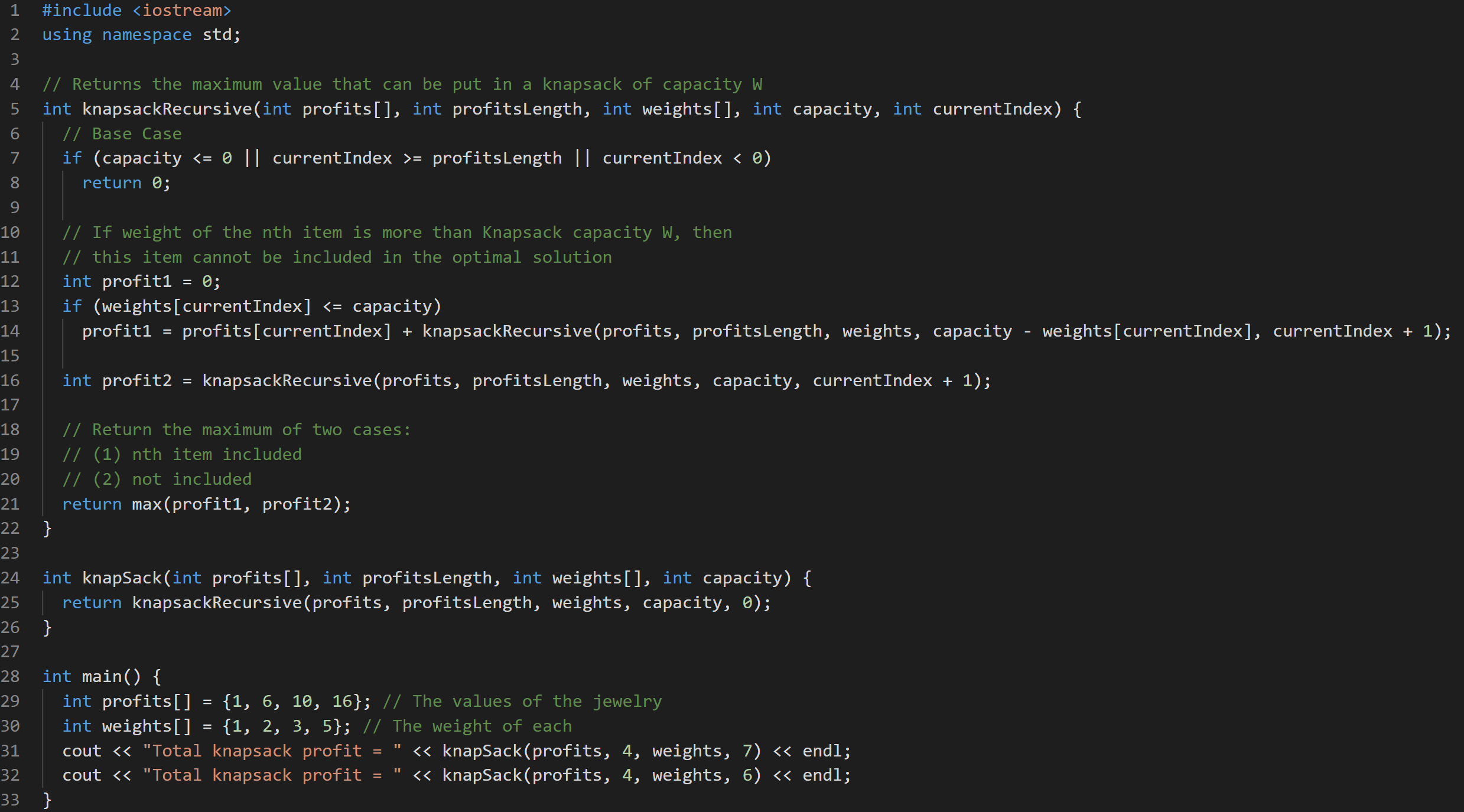
说明
在第 13 和 14 行,我们从 weights 数组的开头开始,检查物品是否在最大容量内。如果是,我们递归地调用 knapsack() 函数并将结果保存在 profit1 中。
然后递归调用相同的函数,排除该物品,并将结果保存在 profit2 变量中。在第 21 行,我们返回 profit1 和 profit2 中较大的一个。
伪代码
下面这段伪代码说明了程序的运行流程。
对于每一个物品 `i`
如果总重量不超过背包容量,则创建一个包含 `i` 的新集合,并递归处理剩余的容量和选项
创建一个没有 `i` 的新集合,然后递归处理其余的物品
从上述两个集合中返回收益更高的一个
这个程序包含许多重复的子问题,但我们并没有把结果存储起来,而是每次都再重新计算一次。重复计算会大大增加程序运行时间。为了避免重复计算,我们可以改用动态规划来保存子问题的解决方法以供之后使用。
最优动态规划解
现在,我们将通过添加自上而下的动态编程来优化递归解决方案,以处理重复的子问题。
由于递归函数 knapsackRecursive() 中有两个变化的值(capacity 和 currentIndex),因此我们可以使用二维数组来存储所有已知子问题的结果。如上所述,我们需要存储每个子数组(即每个可能的索引 i)和每个可能的容量 c 的结果。
这是背包问题在时间和空间复杂度上的最优解。
时间复杂度
O(N*C):记忆表里存储了所有子问题的结果,最多只会有 N∗C 个子问题。
空间复杂度
O(N∗C+N):O(N∗C) 是记忆表的空间,O(N) 是递归调用栈的空间。
小贴士:在面试时,一定要和面试官谈谈你的想法,这样他们才能看到你解决问题的能力。
解决方案
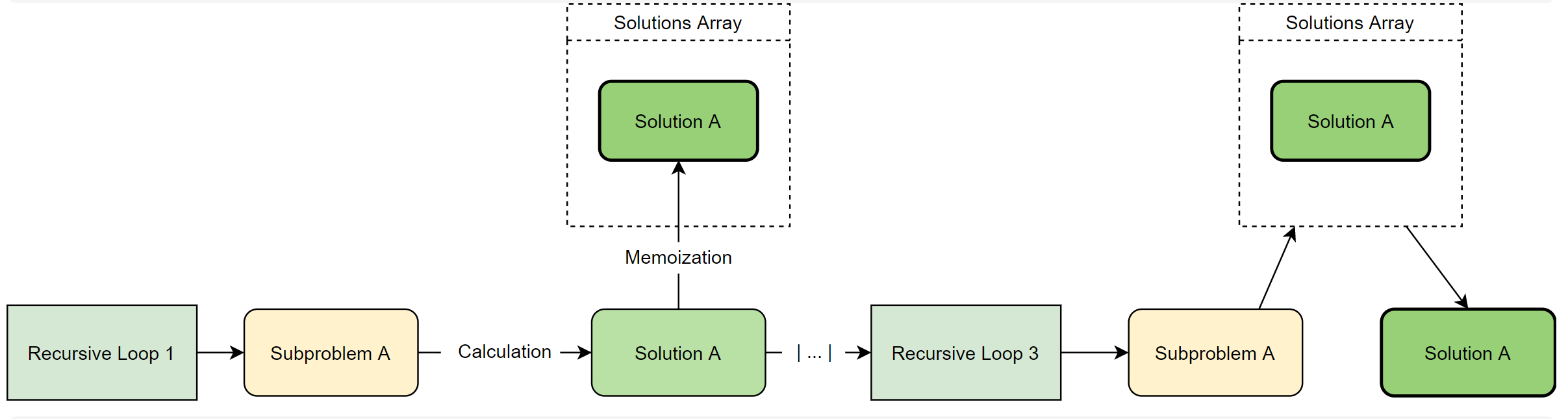
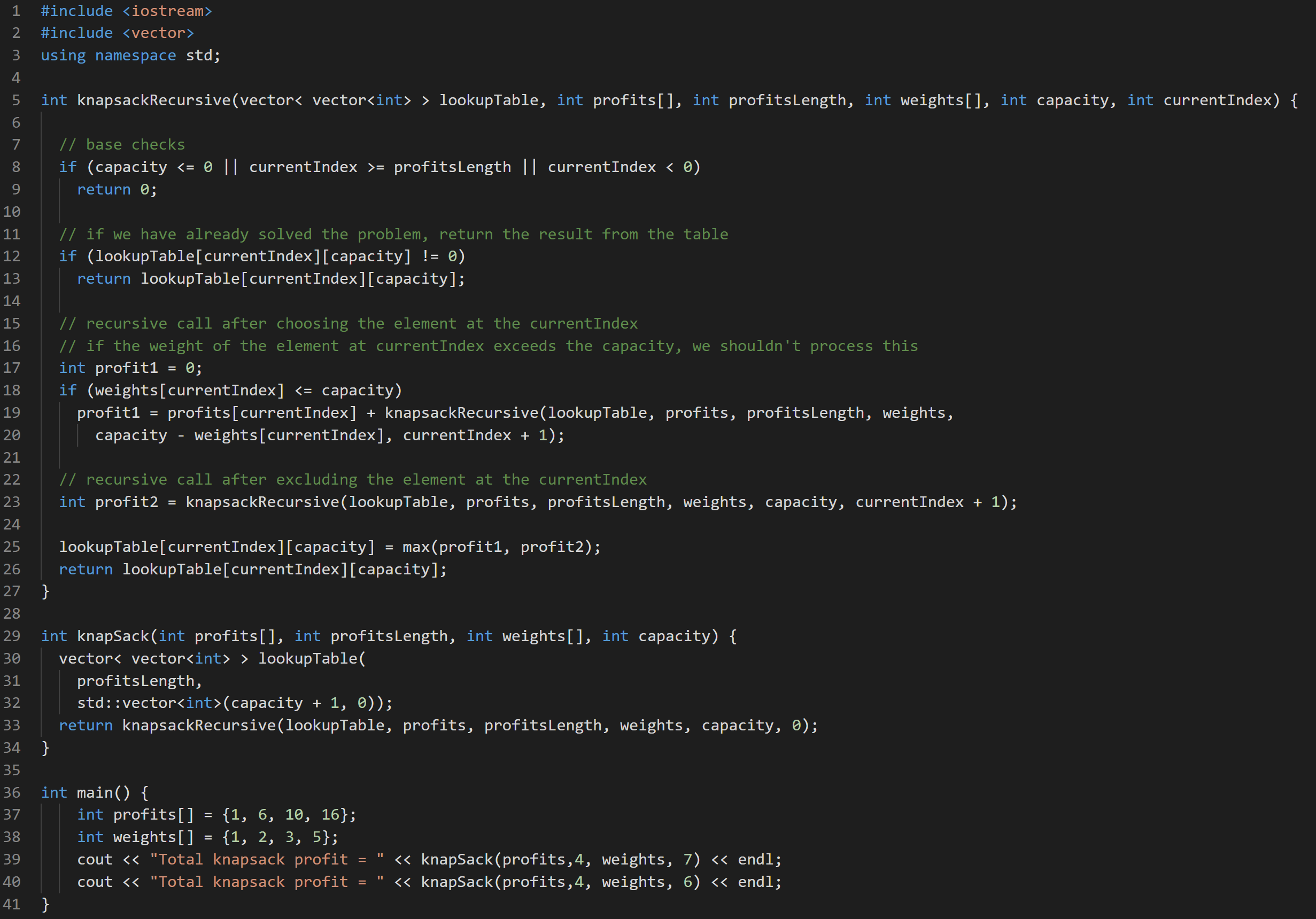
说明
要实现动态规划,我们只需要修改五行代码。
在第 30 至 32 行中,我们创建了一个二维数组 dp,用于保存任何已知子问题的结果。这能让我们在之后将结果记忆化,避免重复计算。
在第 12 和 13 行中,我们添加了一个条件,检查 dp 中是否包含当前子问题的计算结果。如果有,我们直接返回结果并移步至下一个子问题。
在第 38 行中,我们计算如果包含当前物品所能得到的最大价值总值,并保存在 profit1 中;接着计算不包括的情况,并保存在 profit2 中。最后,将二者中较大的一个存放到二维数组 dp 中。
在第 26 行中,我们返回能使背包价值最高的决策,即 profit1 或 profit2。这只是部分的结果,值返回后将开始下一轮的递归调用。当我们把所有可能的组合尝试一遍后,最一开始的的调用将返回整体最优的结果。
接下来要学什么?
感谢你看完了这篇文章。
回答动态编程问题的信心来自于平日的练习和对流行问题变体的接触。在你准备下一次面试的当儿,这里还有一些你需要学习的动态规划问题:
- 最长公共子串
- 最长回文子序列
- 斐波那契数
- 爬楼梯问题
- 硬币兑换问题
祝你面试顺意!
如果发现译文存在错误或其他需要改进的地方,欢迎到 掘金翻译计划 对译文进行修改并 PR,也可获得相应奖励积分。文章开头的 本文永久链接 即为本文在 GitHub 上的 MarkDown 链接。
掘金翻译计划 是一个翻译优质互联网技术文章的社区,文章来源为 掘金 上的英文分享文章。内容覆盖 Android、iOS、前端、后端、区块链、产品、设计、人工智能等领域,想要查看更多优质译文请持续关注 掘金翻译计划、官方微博、知乎专栏。