本文已参与「新人创作礼」活动，一起开启掘金创作之路。

4. 对偶

4.1. Lagrange函数与Lagrange对偶

回到前面提到的标准形式的优化问题(也叫原问题）：

\begin{aligned} min\ \ &f_0(x)\\ s.t.\ \ &f_i(x)\leq 0,i=1,2,\cdots,m\\ &h_i(x)=0,i=1,2,\cdots,p\\ \tag{4-1} \end{aligned}

注意，这里没有要求是凸优化问题。 Lagrange对偶的基本思想是，在目标函数中考虑 $(4-1)$ 的约束条件，即添加约束条件的加权和，得到增广的目标函数，称之为Lagrange函数：

L(x,\lambda,\nu)=f_0(x)+\sum_{i=1}^{m}{\lambda _if_i(x)} + \sum_{i=1}^{p}{\nu _ih_i(x)}\\ \tag{4-2}

注意，Lagrange函数的定义域是 $D\times R^m\times R^p$ ，在后面的讨论中，我们会假设 $\lambda_i\geq 0$ 向量 $\lambda$ 和 $\nu$ 称为对偶变量，或者是问题 $(4-1)$ 的Lagrange乘子向量。 Lagrange对偶函数（自变量为 $\lambda$ 和 $\nu$ ）定义为Lagrange函数关于x取得的最小值：

\begin{aligned} g(\lambda,\nu)&=\mathop{inf}\limits_{x\in D}L(x,\lambda,\nu)\\ &= \mathop{inf}\limits_{x\in D}\left(f_0(x)+\sum_{i=1}^{m}{\lambda _if_i(x)} + \sum_{i=1}^{p}{\nu _ih_i(x)}\right)\\ \tag{4-3} \end{aligned}

Lagrange对偶函数是Lagrange函数的逐点下确界，有个很重要的性质：无论原问题是不是凸的，Lagrange对偶函数都是凹函数。下面分别从理论上进行证明，以及从几何上形象地解释。 理论证明：不难看出， $g(\lambda,\nu)$ 是关于 $\lambda,\nu$ 的仿射函数，为了书写简简洁，我们用一个长的向量 $\mu$ 代表 $(\lambda,\nu)$ 要想证明 $g(\lambda,\nu)$ 是凹函数，只需证明 $\forall \mu_1,\mu_2$ 下式都成立：

g(\theta \mu_1+(1-\theta)\mu_2)\geq \theta g(\mu_1)+(1-\theta)g(\mu_2)\\ \tag{4-4}

下面是证明过程：

\begin{aligned} g(\theta \mu_1+(1-\theta)\mu_2)&=\mathop{min}\limits_{x}L(x,\theta \mu_1+(1-\theta)\mu_2)\\ &=\mathop{min}\limits_{x}\left(\theta L(x, \mu_1)+(1-\theta)L(x, \mu_2)\right)\\ &\geq \mathop{min}\limits_{x}\left(\theta L(x, \mu_1)\right)+\mathop{min}\limits_{x}\left((1-\theta)L(x, \mu_2)\right)\\ &=\theta\mathop{min}\limits_{x}\left( L(x, \mu_1)\right)+(1-\theta)\mathop{min}\limits_{x}\left(L(x, \mu_2)\right)\\ &=\theta g(\mu_1)+(1-\theta)g(\mu_2)\\ \tag{4-5} \end{aligned}

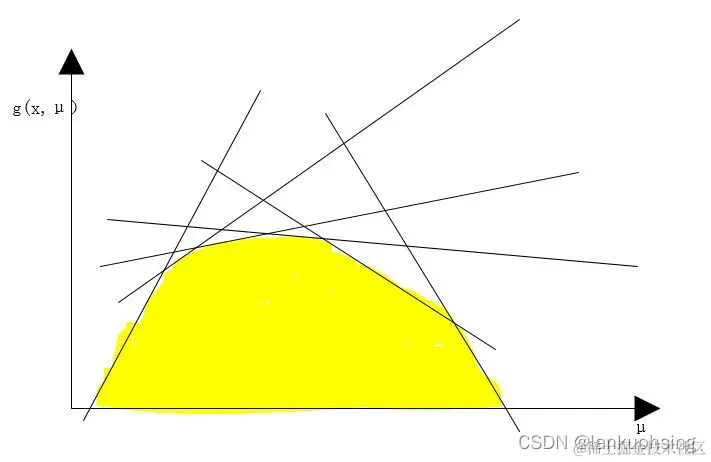
得证！注意，第一步到第二步是因为 $L(x,\mu)$ 是关于 $u$ 的仿射函数；第二步到第三步是因为，地二步中取得最小值时，括号中两项中的 $x$ 是取相同的值的，而第三步中两项分别取最小值不要求 $x$ 一定取相同值（也即能够比第二步涵盖更多情况），因此第三步可能取到的最小值肯定小于或等于第二步的最小值。 几何解释如下：由于 $L(x,\mu)$ 是关于 $u$ 的仿射函数，我们将 $\mu$ 退化为1维来形象地解释。 $L(x,\mu)$ 可以看成是许多的直线簇组成。 $g(x,\mu)$ 可以理解成：当 $\mu$ 取某一个值时，取曲线簇在这个值上的最小值，遍历所有 $\mu$ ，将曲线簇的一些最小值作为 $g(x,\mu)$ 的值域。因此， $g(x,\mu)$ 可以看成下图中黄色区域的边界线，显然是一个凹函数。在这里插入图片描述

此外，Lagrange对偶函数还有如下性质： $\forall \lambda \succeq 0$ (每一维都大于0)和 $\nu$ ，都有

g(\lambda,\nu)\leq p^{\star}\\ \tag{4-6}

其中 $p^{\star}$ 是原问题的最优值。也即，对偶函数构成了原问题的最优值的下界。

4.2. 共轭函数

设函数 $f:R^n\rightarrow R$ ，定义 $f^{\star}:R^n\rightarrow R$ 为：

f^{\star}(y)=\mathop{sup}\limits_{x\in dom\ f}\left(y^Tx-f(x)\right)\\ \tag{4-7}

此函数成为函数 $f$ 的共轭函数。共轭函数是一系列仿射函数的逐点上确界，所以必然是一个凸函数。对于负熵函数 $xlog{x}$ ，它的共轭函数不难推导出是 $f^{\star}(y)=e^{y-1}$ ,这在后面会用到

4.3. Lagrange对偶问题

由 $(4-6)$ 可以看到，对于任意一组 $(\lambda,\nu)$ ，其中 $\lambda \succeq0$ ,Lagrange对偶函数给出了优化问题 $(4-1)$ 的最优值 $p^{\star}$ 的一个下界。我们来看一下从Lagrange函数得到的最好下界。该问题可以表述为如下优化问题：

\begin{aligned} max\ \ g(\lambda,\nu)\\ subject\ to\ \ \lambda\succeq 0 \tag{4-8} \end{aligned}

上述问题被称为原问题的Lagrange对偶问题。满足 $\lambda \succeq 0$ 和 $g(\lambda,\nu)>-\infty$ 的一组 $(\lambda,\nu)$ 被称为一组对偶可行解。如果一组 $(\lambda^{\star},\nu^{\star})$ 是对偶问题的最优解，那么称它是对偶最优解或者最优Lagrange乘子。由于 $g(\lambda,\nu)>-\infty$ 必然是凹函数，且约束条件是凸函数，所以问题 $(4-8)$ 必然是一个凸优化问题。因此Lagrange对偶问题是一个凸优化问题，与原问题的凸性无关

记Lagrange对偶问题的最优值为 $d^{\star}$ ，原问题的最优值为 $p^{\star}$ 。显然有 $d^{\star}\leq p^{\star}$ ，这个性质称为弱对偶性。无论原问题是不是凸问题无论原问题和对偶问题的最优值是否有上下界，弱对偶性都存在。

4.4. 强对偶性与Slater约束准则

如果前面的有 $d^{\star}=p^{\star}$ ，则强对偶性成立。对于一般情况的优化问题，强对偶性一般不成立。如果玉啊为图是凸问题，强对偶性一般存在（但不总是）。强对偶性成立的一个简单的约束条件（Slater条件）是：存在一点 $x\in relint\ D$ 使得下式成立：

f_i(x)< 0,i=1,\cdots,m,\ \ Ax=b\\ \tag{4-9}

满足上述条件的点也称为严格可行点 如果不等式约束函数中有一些是仿射函数时，Slater条件可以进一步改进为：不是仿射函数的那些不等式约束函数需要满足 $(4-9)$ 。换言之，仿射不等式不需要严格成立。例如，假设 $f_1,f_2,\cdots,f_k$ 是仿射函数，则Slater条件可变为：存在一点 $x\in relint\ D$ 使得下式成立：

f_i(x)\leq 0,i=1,\cdots,k,f_i(x)< 0,i=k+1,\cdots,m,Ax=b\\ \tag{4-10}

由此可以得到一个推论：当所有约束条件是线性等式或线性不等式且 $dom\ f_0$ 是开集时，上述改进的Slater条件其实就是可行性条件。也即只要问题是可行的，强对偶性就成立。 Boyd的《Convex Optimization》一书中的5.3.2，证明了当原问题是凸问题且Slater条件成立时，强对偶性成立。

4.5. 最优性条件

注意，此小节讨论的问题并不要求是凸问题。

4.5.1. 互补松弛性

如果强对偶性成立，则有：

\begin{aligned} f_0(x^{\star})&=g(\lambda^{\star},\nu^{\star})\\ &=\mathop{inf}\limits_{x}\left(f_0(x)+\sum_{i=1}^{m}{\lambda _i^{\star}f_i(x)} + \sum_{i=1}^{p}{\nu _i^{\star}h_i(x)}\right)\\ &\leq f_0(x^{\star})+\sum_{i=1}^{m}{\lambda _i^{\star}f_i(x^{\star})} + \sum_{i=1}^{p}{\nu _i^{\star}h_i(x^{\star})}\\ &\leq f_0(x^{\star})\\ \tag{4-11} \end{aligned}

上式可以得到几个有用的结论：

由于第三个不等式取等号，说明 $L(x,\lambda^{\star},\nu^{\star})$ 在 $x^{\star}$ 处取得局部最小值，也即该点处导数为0
$\lambda_i^{\star}f_i(x^{\star})=0,i=1,2,\cdots,m$ ，这个称为互补松弛条件，意味着在最优点处，不等式约束要么取等号 $(f_i(x^{\star})=0)$ ，要么它对应的Lagrange乘子为零 $\lambda_i^{\star}=0$

4.5.2. KKT最优性条件

这小节讨论的目标函数 $f_0$ 和约束函数 $f_1,f_2,\cdots,f_m,h_1,h_2,\cdots,h_p$ 是可微的，但并不要求它们都是凸函数。结合上一小节的内容，我们可以推出，对于目标函数和约束函数可微的任意优化问题，如果强对偶性成立，则任一原问题的最优解 $x^*$ 和对偶问题的最优解 $(\lambda^*,\nu^*)$ 必须满足下列的式子：

\begin{aligned} f_i(x^{\star})&\leq 0 ,i=1,2,\cdots,m\\ h_i(x^{\star})&=0,i=1,2,\cdots,p\\ \lambda_i^{\star}&\geq 0,i=1,2,\cdots,m\\ \lambda_i^{\star}f_i(x^{\star})&=0,i=1,2,\cdots,m\\ \nabla f_0(x^{\star})+\sum_{i=1}^{m}{\lambda _i^{\star}\nabla f_i(x^{\star})} &+ \sum_{i=1}^{p}{\nu _i^{\star}\nabla h_i(x^{\star})}=0\\ \tag{4-12} \end{aligned}

上式被称为非凸问题的KKT条件：对于目标函数和约束函数可微的任意优化问题，如果强对偶性成立，那么任意一对原问题最优解和对偶问题最优解必须满足KKT条件。

凸问题的KKT条件：如果原问题是凸问题，则满足KKT条件的点也是原、对偶问题的最优解。这个定理很重要！上述定理的证明：前面两个条件说明了 $x^{\star}$ 是原问题的可行解；因为 $\lambda^{\star}\geq 0$ ，所以 $L(x,\lambda^{\star},\nu^{\star})$ 是x的凸函数；最优一个条件说明了Lagrange函数在 $x^{\star}$ 处导数为零，也即Lagrange函数取得全局最小值，因此此时有：

\begin{aligned} g(\lambda^{\star},\nu^{\star})&=L(x^{\star},\lambda^{\star},\nu^{\star})\\ &=f_0(x^{\star})+\sum_{i=1}^{m}{\lambda _i^{\star}f_i(x^{\star})} + \sum_{i=1}^{p}{\nu _i^{\star}h_i(x^{\star})}\\ &=f_0(x^{\star})\\ \tag{4-13} \end{aligned}

上述意味着对偶间隙为0，强对偶性成立，因此得证。

4.5.3. 通过解对偶问题求解原问题

由前面可知，如果强对偶性成立，且存在一个对偶最优解 $(\lambda^{\star},\nu^{\star})$ ，那么任意原问题最优点也是 $L(x,\lambda^{\star},\nu^{\star})$ 的最优解。利用这个性质，我们可以从对偶最优方程中去求解原问题最优解。确切的讲，如果强对偶性成立，对偶最优解 $(\lambda^{\star},\nu^{\star})$ 已知，并且下列问题的解唯一：

min\ f_0(x)+\sum_{i=1}^{m}{\lambda _if_i(x)} + \sum_{i=1}^{p}{\nu _ih_i(x)}\tag{4-12}

（Lagrange函数是严格凸函数时上述最优化问题的解是唯一的），如果上式问题的解是原问题的可行解，那么它就是原问题的最优解；如果它不是原问题的可行解，那么原问题不存在最优解（或者无法达到）。当对偶问题比原问题更容易求解时，上述方法很有意义。具体应用见下文的熵的最大化的例子

5. 利用Lagrange对偶求解最优化问题的例子

5.0. 优化问题的一般解决流程

根据问题，列出目标函数和约束条件
如果问题是凸优化问题，判断能不能直接求解。如果没有约束条件，则可以直接求解（求极值）；如果约束条件比较简单，对目标函数求极值后直接满足约束条件则，则也已解决。否则转到3
当直接求解不方便时，列出Lagrange函数，和Lagrange对偶函数，假设Slater条件成立（强对偶性成立），求取对偶问题的最优解，并代入到Lagrange函数里面求它的最优解，如果Lagrange函数最优解唯一且满足原问题的可行性条件，则就是原问题的最优解

5.1. 熵的最大化问题

这个例子在机器学习中可能会经常遇到。问题描述如下：

\begin{aligned} min\ f_0(x)&=\sum_{i=1}^{n}{x_ilog{x_i}}\\ s.t.\ Ax&\preceq b\\ 1^Tx&=1\\ \tag{5-1} \end{aligned}

定义域为 $R_{++}$ 。上述目标函数其实就是负熵，是凸函数。原问题是凸问题，但是不好直接求解。记目标函数为 $f_0(x)$ ，Lagrange函数为：

\begin{aligned} L(x,\lambda,\nu)=f_0(x)+\lambda^T(Ax-b)+\nu(\vec 1^Tx-1)\\ \tag{5-2} \end{aligned}

Lagrange对偶函数为：

\begin{aligned} g(\lambda,\nu)&=\mathop{inf}\limits_{x}\ \left(f_0(x)+\lambda^T(Ax-b)+\nu(1^Tx-1)\right)\\ &=-b^T\lambda-\nu+\mathop{inf}\limits_{x}\ \left(f_0(x)+(A^T\lambda+\vec 1\nu)^Tx\right)\\ &=-b^T\lambda-\nu-\mathop{sup}\limits_{x}\ \left(-f_0(x)-(A^T\lambda+\vec 1\nu)^Tx\right)\\ &=-b^T\lambda-\nu-f_0^{\star}\left(-(A^T\lambda+\vec 1\nu)\right)\\ \tag{5-3} \end{aligned}

其中 $f_0^{\star}$ 是 $f_0$ 的共轭函数。对于负熵函数 $xlog{x}$ ，它的共轭函数不难推导出是 $f^{\star}(y)=e^{y-1}$ ，因此不难得出 $(5-3)$ 可进一步化为：

\begin{aligned} g(\lambda,\nu)&=\mathop{inf}\limits_{x}\ \left(f_0(x)+\lambda^T(Ax-b)+\nu(1^Tx-1)\right)\\ &=-b^T\lambda-\nu-\sum_{i=1}^{n}e^{\left(-a_i^T\lambda-\nu-1\right)}\\ \tag{5-3} \end{aligned}

假设原问题可行，也即Slater条件成立（注意这里的约束条件都是仿射函数），那么此时强对偶性成立。因此对Lagrange函数求最小值即可求得原问题的最小值解。注意到Lagrange函数是严格凸函数，很容易求得最小值点（是唯一的）

x_i^{\star}=exp\left(-(a_i^T\lambda^{\star}+\nu^{\star}+1)\right),i=1,2,\cdots,n\\ \tag{5-4}

其中 $a_i$ 是 $A$ 的列向量，如果 $x^{\star}$ 是原问题的可行解，则必定是原问题的最优解；否则说明原问题的最优解不可达到

5.2. 线性规划问题

原问题：

\begin{aligned} min\ \ &c^Tx\\ s.t.\ &Ax=b\\ &x\succeq 0\\ \tag{5-5} \end{aligned}

Lagrange函数：

L(x,\lambda,\mu)=-b^T\nu+(c+A^T\nu-\lambda)^Tx\tag{5-6}

Lagrange对偶函数：

\begin{aligned} g(\lambda,\nu)&=\mathop{inf}\limits_{x}L(x,\lambda,\nu)\\ &=\left\{ \begin{aligned} &-b^T\nu, \ \ A^T\nu-\lambda+c=0 \\ & -\infty,\ \ others \\ \end{aligned} \right.\\ \tag{5-7} \end{aligned}

注意：线性函数只有恒为零时才有下界（零，上界也是零），否则为负无穷（没有下界）。 Lagrange对偶问题：

\begin{aligned} max\ \ &-b^T\nu\\ s.t.\ &A^T\nu-\lambda+c=0\\ &\lambda\succeq 0\\ \tag{5-8} \end{aligned}

等价于:

\begin{aligned} min\ \ &b^T\nu\\ s.t.\ &A^T\nu+c\succeq 0\\ \tag{5-9} \end{aligned}

凸优化基础知识笔记-凸集、凸函数、凸优化问题（二）