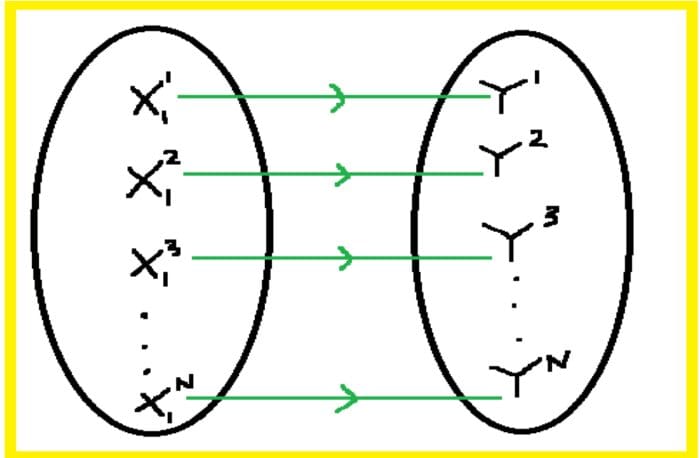
图片由作者提供

关键的经验之谈

• 大多数对进入数据科学领域感兴趣的初学者总是担心数学要求。
• 数据科学是一个非常量化的领域，需要高级数学。
• 但要想入门，你只需要掌握一些数学题目。
• 在这篇文章中，我们将讨论函数在数据科学和机器学习中的重要性。

函数

大部分的基础数据科学都集中在寻找 特征 (预测变量)和一个 目标变量(结果).预测变量也被称为 独立变量，而目标变量是 因果变量.

函数的重要性在于，它们可以用于预测目的。如果能找到描述X和y之间关系的函数，即y=f（X），那么对于 X的任何新值，就可以预测y的相应值。

为简单起见，我们将假设目标变量为连续值，也就是说，我们将专注于一个回归问题。本文讨论的相同原则将适用于分类问题，其中目标变量只采取离散变量，例如0或1。在这篇文章中，我们将重点讨论线性函数，因为它们是数据科学和机器学习中大多数线性模型的基础。

1.有一个预测变量的线性函数

我们假设有一个一维数据集，包含一个单一的特征（X）和一个结果*（Y*），并假设数据集中有N个 观测值。

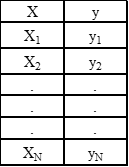
表1.简单的一维数据集，只有一个预测变量。

我们的目标是找到X和Y 之间的关系。首先要做的是生成一个散点图，可以告诉我们X和Y之间的关系类型。例如，使用游轮数据集 巡航_船舶信息.csv的数据集，X=船舱，Y=船员，散点图看起来像这样。

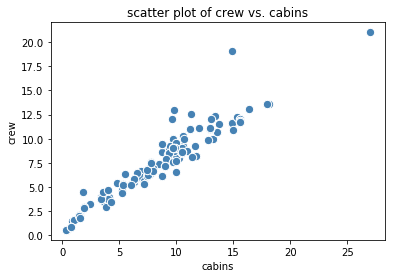
图1.船员与舱位的散点图 | 作者图片

从图1中，我们观察到预测变量*（舱位*）和目标变量*（船员*）之间存在近似的线性关系。拟合数据的简单线性模型如下。

其中w0和w1是使用简单线性回归可以得到的权重。当进行简单线性回归时，输出结果如图2所示，R2分数为0.904。

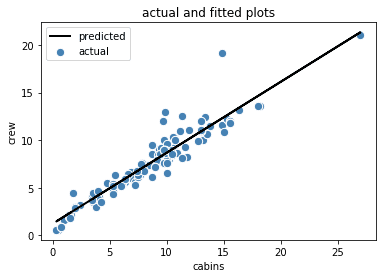
图2.船员与舱室的实际和拟合图 | 作者供图

有时，预测变量和目标变量之间没有明显的可预测关系。在这种情况下，不能用函数来量化这种关系，例如，如下图3所示。

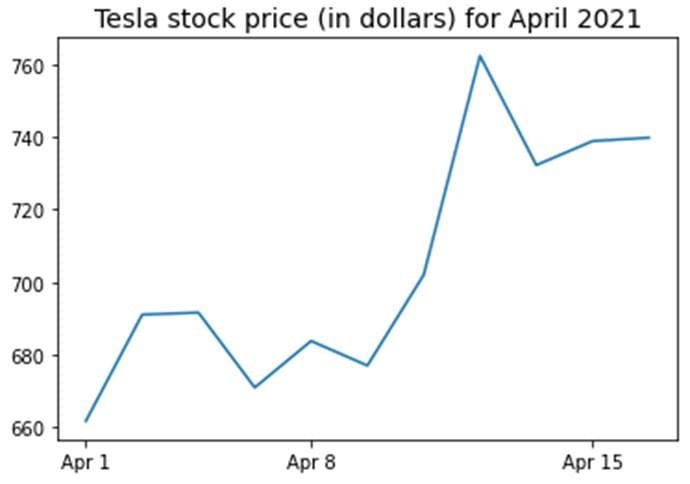
图3.特斯拉2021年4月前16天的股票价格 | 作者的图片

2.有几个预测变量的线性函数

在前面的例子中，我们用X=舱位，Y=船员。现在假设我们想使用整个数据集（见表1）。

表2：显示了邮轮_info.csv数据集的前5行。

那么在这种情况下，我们的预测变量是一个向量X=（年龄、吨位、乘客、长度、舱位、乘客密度）， 而 y=船员。

由于我们的目标变量现在取决于6个预测变量，我们需要计算和可视化协方差矩阵，看看哪些变量与目标变量密切相关（见图4）。

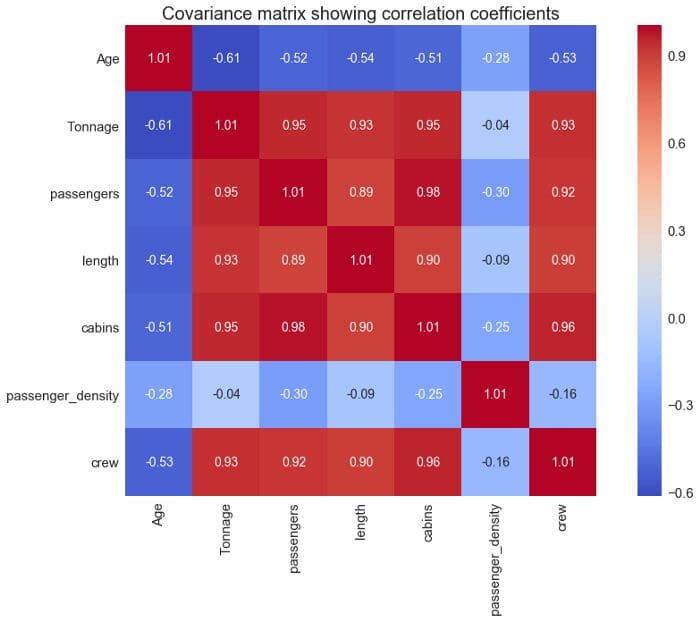
协方差矩阵图显示相关系数

从上面的协方差矩阵图**（图4**），我们看到 "船员"变量与4个预测变量密切相关（相关系数为0.6）。X=（吨位、乘客、长度、舱位）。因此，我们可以建立一个形式的多元回归模型。

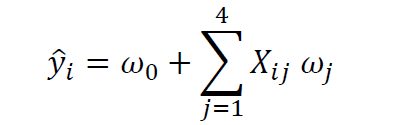
其中X是特征矩阵，w0是截距，w1、w2、w3和w4是回归系数。关于这个问题的多元回归模型的完整python实现，请看这个GitHub仓库：https://github.com/bot13956/Machine_Learning_Process_Tutorial

总结

• 大多数数据科学问题都可以归结为找到描述特征变量和目标变量之间关系的数学函数。

• 如果这个函数可以被确定，那么它就可以被用来预测给定预测值的新目标值。

• 大多数数据科学问题都可以被近似为线性模型（单一或多个预测变量）。