使用解复用器的全加器
改进文章
保存文章
喜欢的文章
- 最后更新: 2022年6月7日
全加器是一个组合电路,它计算总和并输出两个输入位和一个输入进位。因此,它有三个输入--两个比特A和B,以及输入进位Cin,和两个输出--总和S和输出进位Cout。
在这篇文章中,全加器电路是通过使用解复用器的概念实现的。通过使用全加器的真值表,我们将一个解复用器与两个OR门连接起来,它对三个比特进行加法运算,并产生输出的和与进位。
全加器的真值表。
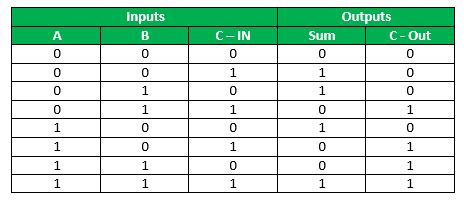
从真值表中,我们可以把总和S和结转Cout表示为。
S(A, B,Cin)= (A'B'C) + (A'BC') + (AB'C') +(ABC)
Cout(A,B,Cin)=(A'BC)+(AB'C)+(ABC')+(ABC)
即为。
S(A,B,Cin) = ∑(1,2,4,7)
Cout(A,B,Cin) = ∑(3,5,6,7)
现在,我们将用一个解复用器来实现这些SOP表达式。
实现。
在多路复用器中实现一个布尔函数的步骤。
- 首先,找出输入变量的数量。如果是3个变量的函数,那么我们需要一个1:8的复用器。如果是n个变量函数,我们需要一个1:2n的复用器。
- 把变量作为多路复用器的选择线。一个1:2n多路复用器将有n条选择线。
- 现在,从函数的真值表中找出最小项,抓住解复用器的相应输出线,并将其放入OR门。这确保了只要函数的任何一个小项为高,输出就为高。
使用解复用器的全加器。
我们有两个输出,因此有两个函数S和Cout。显然,我们需要使用一个1:8的解复用器。利用上述步骤,我们可以看到,对于S,我们需要将解复用器的第1、2、4和7行放到一个OR门上。对于Cout,我们有一个OR门,第3、5、6和7行。
最终的实现如下。

使用解复用器的全加器
我的个人笔记arrow_drop_up
保存
