高校投资方案与资产管理的解决方案（网页版）

摘要

在如今，高校通常会有大量资金，而如何科学的利用和管理这些资产就显得格外重要。本文通过构建运筹学的线性规划模型并以我校校友会的300万元为例来科学的进行投资。我们首先先从不同年期的储蓄入手，通过我们构建的模型以及查阅的资料可得每年发放奖励与助学金共647338.5元。其次我们又考虑了中、高风险投资----国债和基金。通过我们构建的模型以及查阅的资料可得每年发放奖励与助学金共249725.8元。最后我们考虑到利率是有波动的，因此我们通过蒙特卡罗模拟法模拟出波动，并通过线性回归找出利率与助学金浮动比例间的关系，最终我们得到了两者之间的一次函数，以方便决策计算。

【关键词】投资方案基金增值连续线性规划模型线性回归蒙特卡罗模拟法

问题重述

（1）某学校获捐M元RMB，这些钱在某银行存款，年利率如表1，需要在往后五年里，每年把本息以等额的方法进行资助贫困生和奖励优等生，制定详细的存款方法，并且得出年度的资助和奖励金额。

表1 存款年利率表

（2）该校与银行协作，也建立M元的基金，若存款，年利率将增加20%；若购买国债，年利率如表2，且在四月份初推出国债的方案。如果此后需要每年把利息以等额的方式进行年度资助和奖励，十年后基金M元增值5%，建立金融投资方案模型以及算出年度资助和奖励金额。

表2 国债年利率表

（3）对于以上问题，若利率不固定，银行会依据国家的经济状况作出调整；学校也会根据具体情况对资助与奖励金额进行范围在上下10%之间的调整，需建立数学模型解决该问题。

问题分析

问题一

根据题意，学校有M元的基础资金，并把它存在某银行，在五年里，根据银行的年利率进行以年为单位存款和提款，每年把本息以等额的方式对学生进行资助金和奖励金的发放。目前已知的是基础资金M元和该银行每年存款的年利率，因为是年初存款，到年末有收益，所以不考虑活期存款，还应在第五年把剩下的本息用等额的方式给学生发放资助金和奖励金。

针对上述目标，我们假设第一年都可以把资金M元进行存款，例如第一年就可以进行一年期、两年期、三年期和五年期四种年限的存款，到时间再取款，把取出来的钱部分按等额的方式发放年度资助和奖励金，剩下的再进行第二年的存款，直到第五年年末把所有的本息都发放。我们确定了运用连续线性规划的方法结合LINGO软件对该问题进行求解，从而得到最好的存款及发放资助金和奖励金的方法，为第二问的求解奠定了基础。

问题二

在第一个问的基础上，问题二中增加了购买国债的选择条件。学校和银行协作，那么每年存款的年利率和活期的利率将增加20%，十年后基础资金将增值5%。题目中设基础资金为M元，我们假设M为300万元，且每一年的四月份开始存款，第二年的四月份取款发放资助金和奖励金，假设发放奖励金和资助金的时间为十年。

根据上述的假设和条件，我们在四月份把M元的基础资金进行银行存款以及购买国债，并把每年所投资国债的部分进行活期存款以满足利润最大化。在前五年，分别都进行一年期、两年期、三年期、五年期银行存款以及三年期和五年期国债的购买。从第六年开始就不再购买为期五年的国债。由问题一可知，后一年的存款总数是前一年总的收益与发放奖励金和资助金的金额之差。构建全等方程，采用联系线型规划的方法列出公结合LINGO进行计算，从而得到答案。

问题三

在第一问和第二问的基础上，第三问增加了利率的不固定性，银行会依据国家经济情况作出调整，随之资助金与奖励金也会在范围90%～110%之间进行调整，因为在这一题中存在数据的缺失问题，所以我们运用了蒙特卡罗模拟的方法，按照正态分布来模拟出利率浮动的倍数，从而得出利润，根据宏观经济学的原理，如果利率增大，则说明物价上涨，则优先在0到10%之间上调贫困生的资助金；利率减小则说明物价下降，则优先在-10%到0之间上调贫困生的资助金。按照这样模拟出缺失的数据，再做出一个以y是浮动比例、x是利率的线性回归来解决这一问题。

模型假设

学校基金在第一年初到位
学校每年发放奖励金额时间都是在每年末
通货膨胀率忽略不计
前两小问银行存款年利率和国债年利率在10年内基本不变
国债每次发行都有三年期和五年期
假设M=300万
10年内利率浮动与资助浮动比例均为正态分布
10年内利率与资助浮动比例线性相关

符号说明

模型的建立与求解

问题一

首先我们可知题目要求实现“制定具体存款方案并得到年度资助和奖励金额”这一目标。而通常情况我们希望存款实现利益最大化，并通过题目中制定存款方案以及给出的表1等元素可确定该题目主要为运筹学上的最优化问题。

（@毛浩）

数据的获取

我们以我校某学院的2021级招生人数为例[1]并以国务院网站上查询到的助学金最大标准[2]以及《轮政府扶贫与高等教育贫困生资助工作》中提到的工作人员的贫困生应控制在15%-30%[3]为例。我们则按照贫困生最小比例计算。获取数据如下表。

根据题目所给出信息，利率信息表如下：

模型建立与求解

我们已知下一年的金额是前一年收益的本息减所发奖金与助学金的金额，且第六年所投资的金额应为0。根据《高职数学建模》上的算法[4]以及我们在问题分析中的思考，可以建立如下模型。注意本题中i,j∈Z且j≠4。通过编写LINGO程序，我们得到以下方案： A=647338.5，也就是每年发放奖励与助学金共647338.5元。1年-5年中每年投资方案如下表：

根据以上数据及假设，可得下式以计算奖励金额和助学金额：可得：将A=647338.5代入解得：所以每年应当发放助学金额153000元，奖学金额发放494338.5元。

LINGO代码如下：

max=a;
x1=a11+a12+a13+a14;
x2=a21+a22+a23;
x3=a31+a32+a33;
x4=a41+a42;
x5=a51;
x6=0;
x1=3000000;
(1+r1)*a11-a=x2;
(1+r1)*a21+(1+2*r2)*a12-a=x3;
(1+r1)*a31+(1+2*r2)*a22+(1+3*r3)*a13-a=x4;
(1+r1)*a41+(1+2*r2)*a32+(1+3*r3)*a23-a=x5;
(1+r1)*a51+(1+2*r2)*a42+(1+3*r3)*a33+(1+5*r4)*a14-a=x6;
r1=1.95/100;r2=2.41/100;r3=2.75/100;r4=3/100;

结果分析

结果概况

根据上文中投资方案色阶观察，5年内均不投资活期且第一年时主要投资定期1年期，其他年期辅助投资。第二年只投资定期3年期。

根据以下饼状图可知奖学金与助学金比例约为3:1。

敏感性分析

a_ij变量的Reduced Cost值表如下：

由色阶来看，在第5年改变定期1年变化率最大，剩下为第2年改变定期2年、第3年改变定期1年和3年以及第4年改变定期2年的变化率较大。

结果解读

由于题目要求每年都要有一定资金分配给学生，并且又要保证利益最大化，所以主要以较短期的投资为主。我们看到投资方案中也主要是在第1年储蓄第1年期为主，并以较长期储蓄为辅以增加利益。

问题二

（@毛浩）

数据的获取

根据题意首先计算建立基金后的年利率，计算公式如下：由题目已知w=20%并根据已给出的r_j进行计算。并且题目已给出国债利率信息表如下：最终整理出利率信息表如下：其他数据均同第一小题。

模型建立与求解

由于基金在10年后增值5%，所以我们须令x_11=3150000。延续上一小题思路列出下式。注意本题中i,j∈Z且j≠4。

通过编写LINGO程序，我们得到以下方案： A=249725.8，也就是每年发放奖励与助学金共249725.8元。1年-5年中每年投资方案如下表：

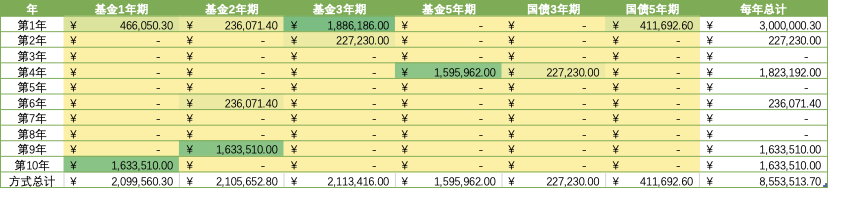根据以上数据及假设，可得下式以计算奖励金额和助学金额：可得：将A=249725.8代入解得：所以每年应当发放助学金额153000元，奖学金额发放96725.8元。

LINGO代码如下：

! 目标函数;
max=a;
! 发放资金限制条件;
x1=a11+a12+a13+a15+b13+b15;
x2=a21+a22+a23+a25+b23+b25;
x3=a31+a32+a33+a35+b33+b35;
x4=a41+a42+a43+a45+b43+b45;
x5=a51+a52+a53+a55+b53+b55;
x6=a61+a62+a63+a65+b63+b65;
x7=a71+a72+a73+b73;
x8=a81+a82+a83+b83;
x9=a91+a92;
x10=a101;
! 保证十年后增值5%;
x11=3150000;
! 设置起始金额;
3000000=y1;
! 每年盈利总额条件;
(1+r1)*a11-a=y2;
(1+2*f2)*a12+(1+f1)*a21-a=y3;
(1+3*f3)*a13+(1+2*f2)*a22+(1+f1)*a31+(1+3*t3)*b13-a=y4;
(1+3*f3)*a23+(1+2*f2)*a32+(1+f1)*a41+(1+3*t3)*b23-a=y5;
(1+5*f5)*a15+(1+3*f3)*a33+(1+2*f2)*a42+(1+f1)*a51+(1+3*t3)*b33+(1+5*t5)*b15-a=y6;
(1+5*f5)*a25+(1+3*f3)*a43+(1+2*f2)*a52+(1+f1)*a61+(1+3*t3)*b43+(1+5*t5)*b25-a=y7;
(1+5*f5)*a35+(1+3*f3)*a53+(1+2*f2)*a62+(1+f1)*a71+(1+3*t3)*b53+(1+5*t5)*b35-a=y8;
(1+5*f5)*a45+(1+3*f3)*a63+(1+2*f2)*a72+(1+f1)*a81+(1+3*t3)*b63+(1+5*t5)*b45-a=y9;
(1+5*f5)*a45+(1+3*f3)*a73+(1+2*f2)*a82+(1+f1)*a91+(1+3*t3)*b73+(1+5*t5)*b55-a=y10;
(1+5*f5)*a55+(1+3*f3)*a83+(1+2*f2)*a92+(1+f1)*a101+(1+3*t3)*b83+(1+5*t5)*b65-a=y11;
y1=x1;y2=x2;y3=x3;y4=x4;y5=x5;y6=x6;y7=x7;y8=x8;y9=x9;y10=x10;y11=x11;
! 基金利率;
f1=2.34/100;f2=2.892/100;f3=3.3/100;f5=3.6/100;
! 国债利率;
t3=3.35/100;t5=3.52/100;

结果分析

结果概况

根据上文中投资方案色阶观察以及下柱状图，投资行为主要集中在第1、4、9、10年。前期投资行为主要倾向于中长期基金投资，而后期投资行为主要倾向于中短期基金投资，整体以国债为辅。根据以下饼状图可知奖学金与助学金比例约为2:3。

敏感性分析

a_ij、b_ij变量的Reduced Cost值表如下：由色阶来看，在第6年改变基金5年变化率最大，较大变化率均集中在第5-7年。本模型并没有考虑投资风险，而投资有风险，决策需谨慎。因此若需要规避风险可以尝试选择敏感性分析中变化率比较大的方案代替。

问题三

（@杨昊霖）

数据的获取

为方便编写Python代码，我们利用如下方法计算资助浮动比例以及利率。根据假设8，可得下式：通过调用Python的NumPy库以及Pandas库，利率浮动倍数与资助浮动比例分别以15、20为种子数按照正态分布随机生成。具体数据见附件。

再通过Excel对生成数据进行线性回归分析，并使用Python的Seaborn库可视化。拟合结果如下式：拟合效果图如下：在利率变化时可直接按照该函数计算助学金浮动比例，即可算出结果。

python脚本如下：

#%%
from matplotlib import rcParams
import pandas as pd
from numpy import *

df = pd.read_csv('年利率.csv')
rate = array([df.年利率 / 100]).T
random.seed(15)
random_multiple = random.uniform(-0.5, 0.5, (1, 10)) + 1
rate_10 = random_multiple * rate
random.seed(20)
add_pct = random.uniform(0, 0.1, (6, 10))
minus_pct = random.uniform(-0.1, 0, (6, 10))
support = (random_multiple > 1) * ones((1, 6)).T * add_pct + (random_multiple < 1) * ones((1, 6)).T * minus_pct
pd.DataFrame(support, columns=range(1,11)).to_csv('蒙特卡罗模拟十年内助学金占比浮动大小.csv')
pd.DataFrame(rate_10, columns = range(1, 11)).to_csv('蒙特卡罗模拟十年内年利率.csv')
#%%
from seaborn import *
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS']
y = support.flatten()
x = rate_10.flatten()
df = pd.DataFrame(list(zip(x ,y)))
df.columns = ['利率', '助学金浮动比例']
df.to_csv('整体拟合原始数据.csv')
lmplot(x = '利率', y = '助学金浮动比例', truncate = True, data = df)
plt.title('拟合效果图')
plt.tight_layout()
plt.savefig('img1.jpeg', dpi = 600)

结果分析

通过使用Excel进行线性回归，得到数据如下在回归结果中调整R^2=0.4600491，说明拟合优度尚可。F检验中F并不大于临界值，可能受样本量限制，但影响不大，对应概率P值远小于0.001，回归方程整体十分显著。截距与变量x_1对应的t检验概率P值均小于0.001，均十分显著。

模型的评价与推广

优点

（1）问题一中运用到了连续线性规划的方法，将利率可以较好的展现出具体的存款方法以便于更好的发放奖学金和资助金。

（2）问题二中联系了国债推出的时间问题，所以将基金的存钱日期与发放奖学金、资助金的日期都往后推迟，简便了计算的步骤、增加了答案的可行性。

（3）问题三中运用了蒙特卡罗模拟的方法，模拟出利率浮动的倍数，为第三题缺失的数据弥补了空缺。

（4）问题三中联系到了宏观经济学的原理，优先考虑资助金的发放问题。

（5）模型在一定程度上准确且巧妙的描述了问题，且对其进行了一定的简化。

缺点

（1）模型存在近似误差，是通过拟合产生的。

（2）国家的经济情况具有不确定性，难以准确的通过模型进行预测。

推广

（1）对于股票的购买，股票的上涨和下跌的不确定情况，可类比问题三中因国家经济情况不稳定而造成的银行利率不固定的问题，从而更好地预测出在什么时候更合适买卖股票，具有实用性。

（2）在企业中的企业决策与资金分配管理问题，比如在科研、宣传、人力等方的资金分配可以类比文章的线性规划模型，以得到更好的解决方案，具有可行性。

（3）可以运用在投资方面的问题上，结合文章中在第二问对国债和银行存款的选择上建立的模型来推测出应如何投资才能使利益最大化。

参考文献

[1]北京联合大学2021年招生简章 [R],北京联合大学,2021. www.bec.buu.edu.cn/art/2021/5/…

[2]国务院关于建立健全普通本科高校高等职业学校和中等职业学校家庭经济困难学生资助政策体系的意见[R],中国国务院,2007.www.gov.cn/zhuanti/201…

[3]孟祥韵.论政府扶贫与高等教育贫困生资助工作[J].现代商贸工业,2018,39(32):164-165.DOI:10.19311/j.cnki.1672-3198.2018.32.082.

[4]郭培俊.高职数学建模[M].杭州:浙江大学出版社,2010.12