持续创作,加速成长!这是我参与「掘金日新计划 · 6 月更文挑战」的第11天,点击查看活动详情
题目
给定一个单链表的头节点 head ,其中的元素 按升序排序 ,将其转换为高度平衡的二叉搜索树。
本题中,一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差不超过 1。
示例 1
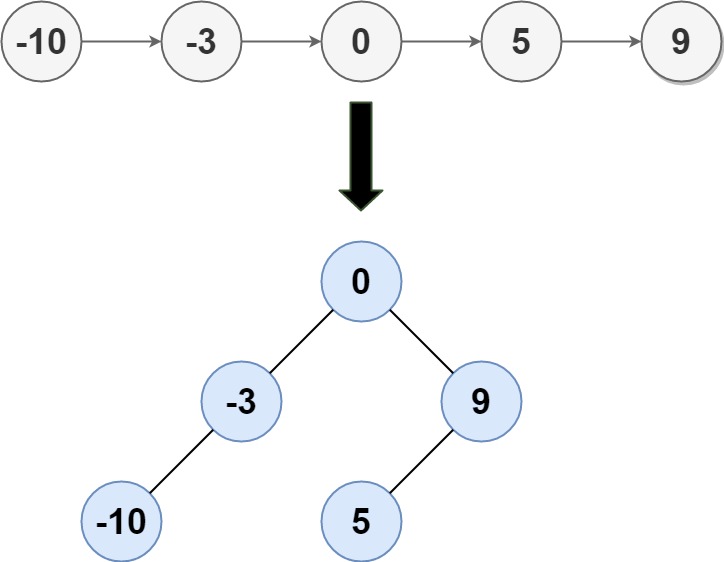
输入: head = [-10,-3,0,5,9]
输出: [0,-3,9,-10,null,5]
解释: 一个可能的答案是[0,-3,9,-10,null,5],它表示所示的高度平衡的二叉搜索树。
示例 2
输入: head = []
输出: []
提示
head中的节点数在[0, 2 * 104]范围内- -10^5 <= Node.val <= 10^5
题解
思路
我们首先需要知道三点:
- 对于每个节点互不相同的二叉搜索树而言,其中序遍历是一个严格递增的序列
- 一棵完全二叉搜索树也一定是一颗平衡二叉树
- 节点总数为 n
代码思路:
- 由于给出的是一个链表,为了便于后续操作,先利用了一定的空间将遍历后得到序列存了起来。我们假设根节点的序号为 0,其左右孩子的序号分别为 1、2,即以层次遍历的方式进行标号。对于编号为 i 的节点而言,如果 2i+1<n,则为左孩子编号; 2i+2 < n,则为右孩子编号
- 我们采取中序遍历,其本质就是往长度为 size 的数组里面填已知的序列,只不过要 模拟中序遍历的过程 填才能保证是搜索树。从 0 号根节点开始,如果传入的编号 cur >= n,说明上一个节点是没有左或右孩子的,应该返回空指针。同时利用指针来记录 有序序列下一个应填的数。同时在函数结尾返回当前节点,实现树的构建操作
代码
class Solution {
public:
vector<int> nums;
int idx = 0, n = 0;
TreeNode* sortedListToBST(ListNode* head) {
ListNode* p = head;
while(p){
nums.emplace_back(p->val);
p = p->next;
++n;
}
return dfs(0);
}
TreeNode* dfs(int cur){
if(cur >= n) return nullptr;
TreeNode* root = new TreeNode(0);
// 中序遍历的标准代码
root->left = dfs(2*cur+1);
root->val = nums[idx++];
root->right = dfs(2*cur+2);
return root;
}
};
结语
业精于勤,荒于嬉;行成于思,毁于随。