如何在Python中用基于角度的技术检测离群值

今天你吸猫了么
245 阅读7分钟

Detecting Outliers with Angle-based Techniques in Python

基于角度的异常值检测（ABOD）是检测给定数据集中的异常值或异常值的流行技术之一，在实际工作中经常用于多变量环境。它是检测异常值的几何方法体系的一部分。这方面的其他方法包括基于深度的技术，它是在凸壳的概念上发展起来的。在这篇博客中，我们将只关注ABOD，它的理论和一个使用PyOD python包实现它的简短教程。但在此之前，让我们来定义一个离群点。任何持有与数据集中大多数观察值截然不同的属性的观察值或数据点都被称为离群点/异常点。数据集中的离群点可能因为许多因素而发生，如仪器记录错误、人为错误、与多数人群的自然变化等。

你可能希望在从事银行业领域的欺诈交易检测、电子商务领域的销售高峰和低谷分析、识别网络中的恶意节点/数据包等用例时检测数据集中的异常。除了那些不一定需要把检测异常值作为最终目标的用例之外，在试图拟合模型以学习大多数数据点所拥有的一般模式时，你可能要考虑处理数据集中的这些数据点。通常情况下，移除异常点的决定取决于开发者，要考虑的事情包括--如果潜在的异常点是人口的自然部分，或者是由于一些工具性错误而产生的，等等。数据中的异常点会导致学习倾斜的数据表示，提供基础数据的误导性表示。因此，在处理这类要点时，有必要通过遵守机器学习模型的假设来更好地适应机器学习模型。

此外，根据这些系统部署的领域的敏感性，保守一点，与假阴性（FN）相比，假阳性（FP）高一点，往往是一种好的做法。这主要是因为在现实世界中，你总是可以通过在循环中加入人类来监督最后的决定。虽然，这可能会增加整体的周转时间，导致审讯次数减少。但这仍然比跳过一个异常点并在之后后悔要好得多。例如--最好是保守一点，阻止任何不寻常的高额付款流出或流入银行账户，然后通过IVR或与客户的正常通话来确认，而不是被骗。

假阳性- 模型说这是一个异常值。但这不是一个异常值。

假阴性--模型说这不是一个离群点。但它是一个离群点。

因此，现在让我们深入了解ABOD和它的变化--详细情况。

基于角度的离群点检测（ABOD）

这项技术是基于关注一组多变量特征空间中的任意三个数据点所形成的角度的想法。角度围度的方差对于离群点和正常点来说是不同的。通常情况下，观察到的离群点的方差要比离群点的方差高，因此这样的测量方法可以帮助我们对正常点和离群点进行不同的分类。基于角度的离群点（ABOD）技术在高维空间中工作得很好，不像其他基于距离的测量方法那样受到 "维度的诅咒"的影响。在高维空间中任何两点之间的距离几乎都是相似的。在这种情况下，角度可以提供更好的接近度的图片。

该算法非常简单，描述如下

  1. 遍历每个数据点，计算它*（枢轴）*与所有其他数据对形成的角度，并将它们存储在角度列表中。
  2. 计算在步骤1中创建的这个角度列表的方差。
  3. 小于某个阈值的方差值可以被标记为潜在的异常现象。(低方差 表示支点是一个 异常, 高方差 表示枢轴点是一个 正常点*)*

让我们也从视觉上理解一下 --

Detecting Outliers with Angle-based Techniques in Python

ABOD图解

从上面的左图可以看出，从视觉上我们看到了2个集群，一个是正常点，另一个是异常点，即单一的蓝色点。如果我们选择红色的点作为兴趣点*（枢轴*），并且我们想看看这个点是否是一个离群点；我们将计算这个点和空间中任何其他两个点所包围的角度。在迭代所有的对子并计算这个支点所包围的角度时，我们可能会观察到角度的很多差异。这样的模式表明，支点是一个具有高内聚力的集群的一部分。

同样，如果我们现在观察右图，把注意力集中在绿色的点上，并重复选择其他任何两点的过程，观察它与支点所围成的角度，我们可能会观察到非常少的差异。这样的模式表明，所关注的点远离大多数集群，有可能是一个异常点。使用基于角度的技术检测异常的整个过程有一个相当高的复杂度，即O(n³)，因为每次我们都需要用一个支点做一个三联体，然后在所有的对上循环，以计算所包围的角度的方差。

一个更快的版本被称为快速ABOD。它使用K-nearest neighbours来近似计算方差，而不是从给定枢轴的所有可能对中计算。随着KNN中 "K "值的增长，该算法收敛到真正的方差，并像其旧版本一样行事。下图显示了快速ABOD如何逼近离群值的说明。

Detecting Outliers with Angle-based Techniques in Python

近似（快速）ABOD

从这两个例子中可以看出，在计算包围的角度时，只考虑了从支点c*（左边是红色，右边是绿色）*开始的k个最近的邻居，这使得它的速度快得惊人。

代码

在博客的这一段，我们将通过一个快速的例子，使用PyOD包检测合成数据集中的异常情况。PyOD是用于检测多变量数据中异常值的最全面和可扩展的Python工具包之一。它提供了40多种异常值检测算法，从传统技术到使用接近、集合和基于神经网络方法的目标检测领域的最新发展。

你可以使用pip安装PyOD，如下图所示 -

$> pip install pyod

接下来，我们可以使用PyOD的generate_data方法在2-D空间生成150个随机样本。我特别选择了2-D空间，而不是任何更高的值，因为便于可视化。我还将污染率设置为10%，即150个数据点中有15个将是离群值。正如文件中提到的，正常点是通过多变量高斯分布产生的，而离群点是通过均匀分布产生的。

from pyod.utils.data import generate_data

X_train, Y_train = generate_data(   
                                    n_train=150, 
                                    n_features=2,
                                    train_only=True,
                                    contamination=0.1,
                                    random_state=42
                                 )
                                 
x1, x2 = X_train[:,0], X_train[:,1]

让我们来看看数据的分布情况是怎样的 --

import matplotlib.pyplot as plt
%matplotlib inline

for idx, i in enumerate(Y_train):
  if i==0.0: 
    color='blue'
  else: 
    color='red'
  plt.scatter(x1[idx], x2[idx], c=color)

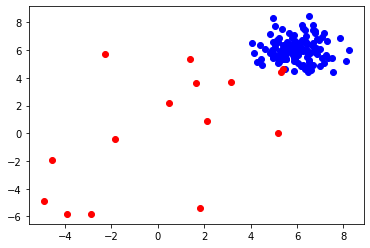
Detecting Outliers with Angle-based Techniques in Python

带有离群值的合成数据（红色标记）。

接下来，我们通过减少N^3的搜索空间来拟合Fast ABOD，以计算只与10个邻居形成的角度。然后我们继续计算误差%。

from pyod.models.abod import ABOD

abod_model = ABOD(contamination=0.1, method='fast', n_neighbors=10)
abod_model.fit(X_train)

pred = abod_model.predict(X_train)

error = (pred != Y_train).sum()
print (f'Error % = {(error/len(pred))*100}')
>> Error % = 2.6666

接下来，我们绘制出对异常值和离群值的预测结果。

import matplotlib.pyplot as plt
%matplotlib inline

for idx, i in enumerate(pred):
  if i==0.0: 
    color='purple'
  else: 
    color='orange'
  plt.scatter(x1[idx], x2[idx], c=color)

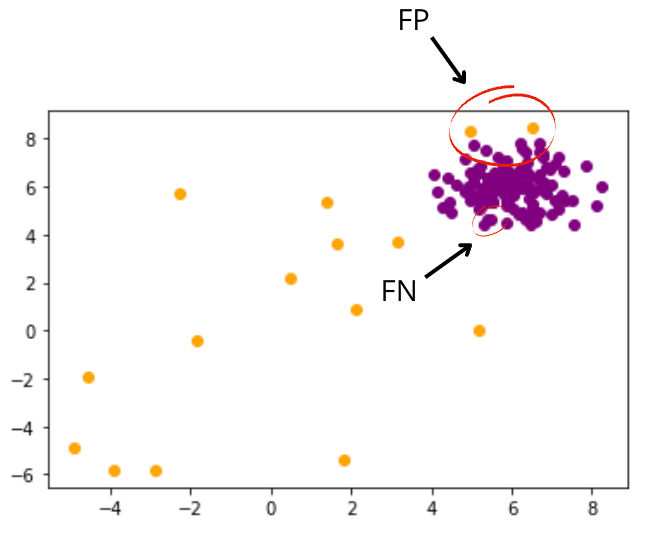
Detecting Outliers with Angle-based Techniques in Python

异常值检测的ABOD预测

从上图中可以看出，橙色和紫色的点分别是预测的离群点和内联点。而我们的模型总共犯了4个错误（2个假阳性，2个假阴性）。

结论性思考

因此，我们对这篇博客进行了总结。请随意查看PyOD库提供的其他算法，并尝试将其中一些算法集合起来以获得最佳效果。人们经常使用的另一种流行的无监督异常检测技术被称为隔离森林。请随时查看这个博客，了解这个概念的精彩演练。

avatar
文章
阅读
粉丝