本文已参与【新人创作礼】活动，一起开启掘金创作之路

机器学习笔记

1、初识机器学习

1.1 什么是机器学习

Arthur Samuel（1959）：使计算机具有学习能力的研究领域

Tom Mitchell（1998） ：一个适当的学习问题定义如下：计算机程序从经验E中学习，解决某一任务T，进行某一性能度量P。通过P测定在T上的表现因经验E而提高。

1.2 监督学习

有标签的学习，利用一组已知类别的样本调整分类器的参数，使其达到所要求的性能的过程。

1.3 无监督学习

无标签的学习，就是只有数据集，不知道这些数据集的结果。需要算法自己学习从而得到正确的结果

无监督学习或聚类算法的应用：

• 组织大型计算机集群
• 社交网络的分析
• 市场细分中的应用
• 天文数据分析

2、单变量线性回归

介绍一些符号

m=训练的样本数量

x=输入的特征值

y=输出变量

2.1 模型描述

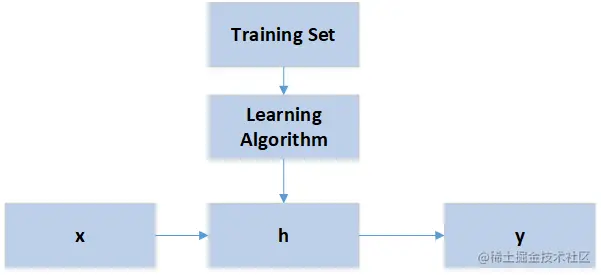
h是一个引导从x得到y的函数，称作假设函数

2.2 代价函数

代价函数也被称作平方误差函数，有时也被称为平方误差代价函数，这是解决回归问题最常用的手段。也有其他一些代价函数可以选择。

如果假设函数是： $h_\theta (x)=\theta_0+\theta_1x$

如果代价函数采用平方误差函数，则代价函数入下

m指的是样本数量，因为是m个样本累加求平方误差，所以最后再除以m，之所以除以2是因为让这个数值更方便计算但是又不影响$\theta_0 和 \theta_1$ 的最终结果。

为了得到预测最准确的假设函数，需要找到一组 $\theta_0 和 \theta_1$ 使代价函数最小。梯度下降算法就是解决这个问题的。

2.3 梯度下降

梯度下降算法寻找最小值：先找到一个初始点，然后计算出这一点在代价函数中的偏导数（可以理解为切线的斜率），然后沿着这个方向寻找下一个点，使代价函数更小，这个过程不断迭代，直到找到最小值。

梯度下降算法可以用下面这个公式

注意：$\alpha$ 是学习率，不能太小，也不能太大，如果太小，收敛慢，需要迭代很多次才能找到最小值。如果太大，可能会越过最小值，永远无法收敛。

3、线性代数回顾

3.1 矩阵和向量

在数学中矩阵是一个按照长方阵列排列的复数或实数集合。 如下面这个例子：

以上是一个2行3列的矩阵。 矩阵的某个元素可以表示为$A_{i,j}$ ，$i,表示第i行，j表示第j列$。

矩阵的维数可以表示为$m \times n$

向量是一个特殊的矩阵，向量是只有一列的矩阵。 如下面这个例子

这个也可以称之为一个四维向量。用$y_i$ 表示第$i$个元素。

3.2 加法和标量乘法

相同维度的矩阵可以相加，将对应位置的元素相加。

这里说的标量是一个实数。将标量与矩阵中的每个元素相乘。

3.3矩阵向量乘法

为了学习矩阵相乘，先学习矩阵向量相乘。即一个矩阵与一个向量相乘

如下面这个例子

矩阵和向量相乘，矩阵的列数应该和向量的行数相等。将矩阵的每一个数据和向量对应元素相乘累加，得到向量的每一个元素的值。

3.4 矩阵乘法

基于上一小节，知道了矩阵和向量的乘法，那矩阵和矩阵相乘可以拆分为矩阵和向量的相乘，每次提取右边的矩阵的一列作为一个向量和左边的矩阵相乘，以此类推，将所有的结果再组合为一个矩阵就是最终的结果。直接看一个例子

拆分为下面两个计算

那最终两个矩阵相乘的结果是

注意，矩阵相乘维度必须匹配。比如$A \times B =C$ 必须满足$A的列数等于B的行数，假设矩阵是 m \times n 维,B是n \times o维，最终C的维度是：m \times o$ 。

3.5 矩阵乘法特征

• 矩阵乘法不符合交换律：$A \times B \neq B \times A$ （ $A、B都不是单位矩阵$）

• 矩阵乘法符合结合律：$(A \times B) \times C=A \times (B \times C)$

• 矩阵和单位矩阵相乘符合交换律 $A \cdot I=I \cdot A$

3.6 一些特殊的矩阵运算

主要介绍矩阵的转置和逆运算

如果一个矩阵行列数相等，这样的矩阵式方阵，只有方阵才具有逆矩阵。

1）逆矩阵

如何求解逆矩阵呢？有许多主流的编程语言和软件都可以。 以Octave为例，输入pinv(A) 就得到结果。

2）转置矩阵

如果矩阵$A$ 是一个$m \times n$ 的矩阵，$B=A^T$,$B$ 是$A$ 的转置矩阵，维度是个$n \times m$ ，$B_{ij}=A_{ji}$

举个例子