Sequence to sequence入门详解:从RNN, LSTM到Encoder-Decoder, Attention, transformer（二）

lankuohsing
68 阅读1分钟

3. RNN的复杂变种

3.1. GRU(Gated Recurrent Unit)

GRU的提出是为了解决RNN难以学习到输入序列中的长距离信息的问题。 GRU引入一个新的变量——记忆单元，简称CC。C⟨t⟩C^{\langle t\rangle}其实就是a⟨t⟩a^{\langle t\rangle} CC的表达式不是一步到位的，首先定义CC的候选值C~\tilde C:

C~⟨t⟩=tanh(Wc[C⟨t−1⟩,x⟨t⟩]+bc)\tilde C^{\langle t\rangle}=tanh\left(W_c[C^{\langle t-1\rangle},x^{\langle t\rangle}]+b_c\right)

更新门：

Γu=σ(Wu[C⟨t−1⟩,x⟨t⟩]+bu)\Gamma_u=\sigma\left(W_u[C^{\langle t-1\rangle},x^{\langle t\rangle}]+b_u\right)

在实际训练好的网络中Γ\Gamma要么很接近1要么很接近0，对应着输入序列里面有些元素起作用有些元素不起作用。

C⟨t⟩=Γu∗C~⟨t⟩+（1−Γu）∗C⟨t−1⟩C^{\langle t\rangle}=\Gamma_u*\tilde C^{\langle t\rangle}+（1-\Gamma_u）* C^{\langle t-1\rangle}

也即输入序列的有些元素，记忆单元不需要更新，有些元素需要更新。

The cat, which already ate ..., was full

cat后面的词直到was之前，都不需要更新CC,直接等于cat对应的CC 可以解决梯度消失的问题.输出层的梯度可以传播到cat处

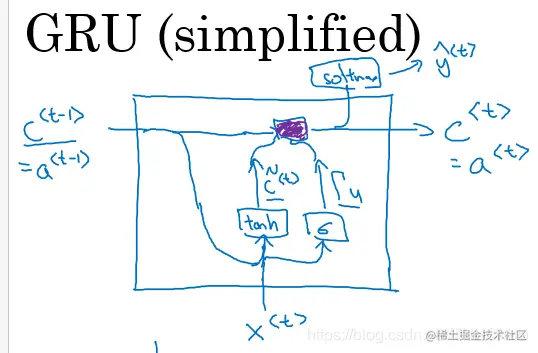
注：CC和Γ\Gamma都可以是想聊，它们在相乘时采用的是element-wise的乘法。当为向量时，与cat的单复数无关的词对应的Γ\Gamma可能有些维度为零，有些维度不为零。为零的维度，是用来保留cat的单复数信息的；不为零的维度可能是保留其他语义信息的，比如是不是food呀之类的 目前讨论的是简化版的GRU，结构图如下 在这里插入图片描述

图3.1GRU的一个基本单元

完整的GRU：

C~⟨t⟩=tanh(Wc[Γr∗C⟨t−1⟩,x⟨t⟩]+bc)Γu=σ(Wu[C⟨t−1⟩,x⟨t⟩]+bu)Γr=σ(Wr[C⟨t−1⟩,x⟨t⟩]+br)C⟨t⟩=Γu∗C~⟨t⟩+（1−Γu）∗C⟨t−1⟩a⟨t⟩=C⟨t⟩(3-1)\begin{aligned} \tilde C^{\langle t\rangle}&=tanh\left(W_c[\Gamma_r*C^{\langle t-1\rangle},x^{\langle t\rangle}]+b_c\right)\\ \Gamma_u&=\sigma\left(W_u[C^{\langle t-1\rangle},x^{\langle t\rangle}]+b_u\right)\\ \Gamma_r&=\sigma\left(W_r[C^{\langle t-1\rangle},x^{\langle t\rangle}]+b_r\right)\\ C^{\langle t\rangle}&=\Gamma_u*\tilde C^{\langle t\rangle}+（1-\Gamma_u）* C^{\langle t-1\rangle}\\ a^{\langle t\rangle}&=C^{\langle t\rangle}\\ \tag{3-1} \end{aligned}

Γr\Gamma_r表示了C~⟨t⟩\tilde C^{\langle t\rangle}和C⟨t−1⟩C^{\langle t-1\rangle}之间的相关程度

3.2. LSTM(Long Short-Term Memory)

没有了Γr\Gamma_r，将1−Γu1-\Gamma_u用Γf\Gamma_f代替

C~⟨t⟩=tanh(Wc[a⟨t−1⟩,x⟨t⟩]+bc)Γu=σ(Wu[a⟨t−1⟩,x⟨t⟩]+bu)Γf=σ(Wf[a⟨t−1⟩,x⟨t⟩]+bf)Γo=σ(Wo[a⟨t−1⟩,x⟨t⟩]+bo)C⟨t⟩=Γu∗C~⟨t⟩+Γf∗C⟨t−1⟩a⟨t⟩=Γo∗tanh(C⟨t⟩)y~⟨t⟩=softmax(a⟨t⟩)(3-2)\begin{aligned} \tilde C^{\langle t\rangle}&=tanh\left(W_c[a^{\langle t-1\rangle},x^{\langle t\rangle}]+b_c\right)\\ \Gamma_u&=\sigma\left(W_u[a^{\langle t-1\rangle},x^{\langle t\rangle}]+b_u\right)\\ \Gamma_f&=\sigma\left(W_f[a^{\langle t-1\rangle},x^{\langle t\rangle}]+b_f\right)\\ \Gamma_o&=\sigma\left(W_o[a^{\langle t-1\rangle},x^{\langle t\rangle}]+b_o\right)\\ C^{\langle t\rangle}&=\Gamma_u*\tilde C^{\langle t\rangle}+\Gamma_f* C^{\langle t-1\rangle}\\ a^{\langle t\rangle}&=\Gamma_o*tanh\left(C^{\langle t\rangle}\right)\\ \tilde y^{\langle t\rangle}&=softmax(a^{\langle t\rangle})\\ \tag{3-2} \end{aligned}

(注意公式里面的Γu\Gamma_u等价于图片中的Γi\Gamma_i)

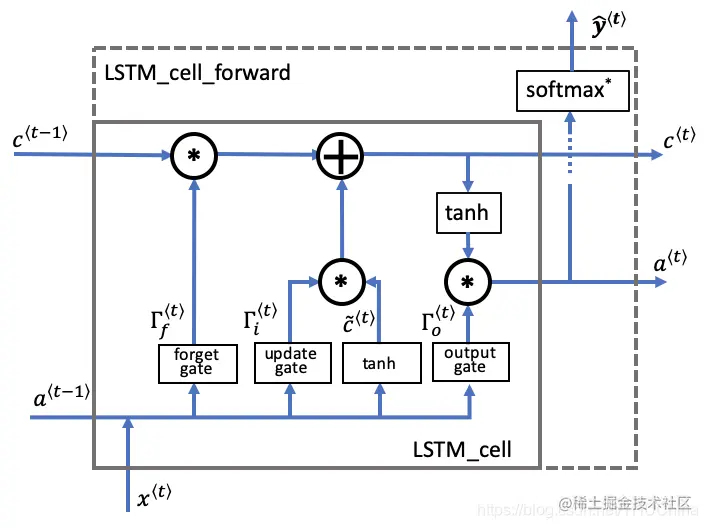
在这里插入图片描述

图3.2 LSTM的一个基本单元

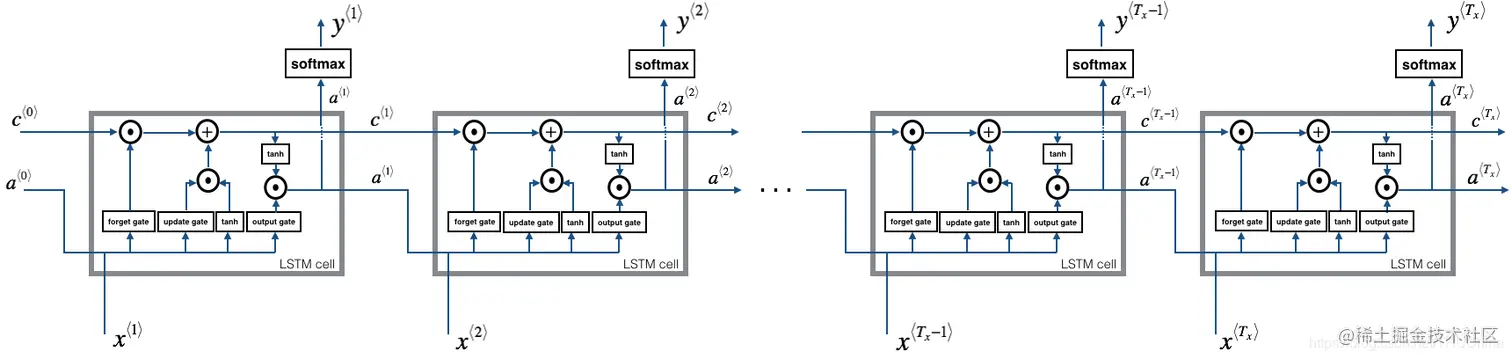
在这里插入图片描述

图3.3 标准LSTM模型-输入维数等于输出维数

3.2.1. peephole连接

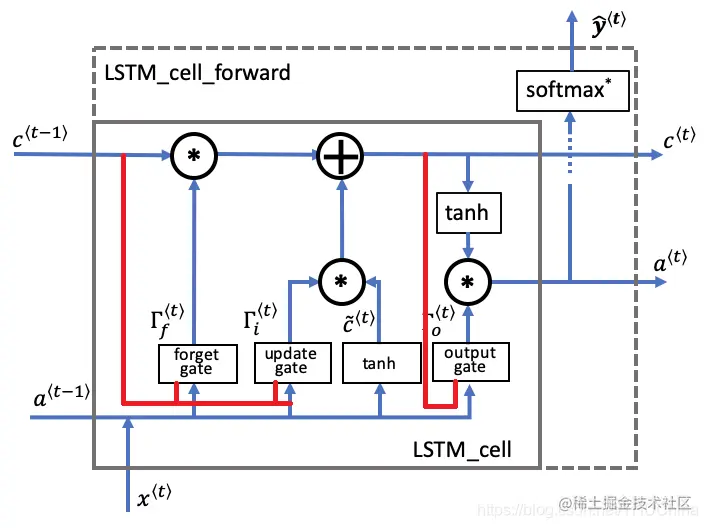
在这里插入图片描述

图3.4 LSTM带有peephole
C~⟨t⟩=tanh(Wc[a⟨t−1⟩,a⟨t−1⟩,x⟨t⟩]+bc)Γu=σ(Wu[c⟨t−1⟩,a⟨t−1⟩,x⟨t⟩]+bu)Γf=σ(Wf[c⟨t−1⟩,a⟨t−1⟩,x⟨t⟩]+bf)Γo=σ(Wo[c⟨t⟩,a⟨t−1⟩,x⟨t⟩]+bo)C⟨t⟩=Γu∗C~⟨t⟩+Γf∗C⟨t−1⟩a⟨t⟩=Γo∗tanh(C⟨t⟩)y~⟨t⟩=softmax(a⟨t⟩)(3-3)\begin{aligned} \tilde C^{\langle t\rangle}&=tanh\left(W_c[a^{\langle t-1\rangle},a^{\langle t-1\rangle},x^{\langle t\rangle}]+b_c\right)\\ \Gamma_u&=\sigma\left(W_u[c^{\langle t-1\rangle},a^{\langle t-1\rangle},x^{\langle t\rangle}]+b_u\right)\\ \Gamma_f&=\sigma\left(W_f[c^{\langle t-1\rangle},a^{\langle t-1\rangle},x^{\langle t\rangle}]+b_f\right)\\ \Gamma_o&=\sigma\left(W_o[c^{\langle t\rangle},a^{\langle t-1\rangle},x^{\langle t\rangle}]+b_o\right)\\ C^{\langle t\rangle}&=\Gamma_u*\tilde C^{\langle t\rangle}+\Gamma_f* C^{\langle t-1\rangle}\\ a^{\langle t\rangle}&=\Gamma_o*tanh\left(C^{\langle t\rangle}\right)\\ \tilde y^{\langle t\rangle}&=softmax(a^{\langle t\rangle})\\ \tag{3-3} \end{aligned}

3.2.2 projection

对隐藏层状态a进行一次线性变换，降低其维数

C~⟨t⟩=tanh(Wc[a⟨t−1⟩,a⟨t−1⟩,x⟨t⟩]+bc)Γu=σ(Wu[c⟨t−1⟩,a⟨t−1⟩,x⟨t⟩]+bu)Γf=σ(Wf[c⟨t−1⟩,a⟨t−1⟩,x⟨t⟩]+bf)Γo=σ(Wo[c⟨t⟩,a⟨t−1⟩,x⟨t⟩]+bo)C⟨t⟩=Γu∗C~⟨t⟩+Γf∗C⟨t−1⟩a0⟨t⟩=Γo∗tanh(C⟨t⟩)a⟨t⟩=Wproja0⟨t⟩+bprojy~⟨t⟩=softmax(a⟨t⟩)(3-4)\begin{aligned} \tilde C^{\langle t\rangle}&=tanh\left(W_c[a^{\langle t-1\rangle},a^{\langle t-1\rangle},x^{\langle t\rangle}]+b_c\right)\\ \Gamma_u&=\sigma\left(W_u[c^{\langle t-1\rangle},a^{\langle t-1\rangle},x^{\langle t\rangle}]+b_u\right)\\ \Gamma_f&=\sigma\left(W_f[c^{\langle t-1\rangle},a^{\langle t-1\rangle},x^{\langle t\rangle}]+b_f\right)\\ \Gamma_o&=\sigma\left(W_o[c^{\langle t\rangle},a^{\langle t-1\rangle},x^{\langle t\rangle}]+b_o\right)\\ C^{\langle t\rangle}&=\Gamma_u*\tilde C^{\langle t\rangle}+\Gamma_f* C^{\langle t-1\rangle}\\ a_0^{\langle t\rangle}&=\Gamma_o*tanh\left(C^{\langle t\rangle}\right)\\ a^{\langle t\rangle}&=W_{proj}a_0^{\langle t\rangle}+b_{proj}\\ \tilde y^{\langle t\rangle}&=softmax(a^{\langle t\rangle})\\ \tag{3-4} \end{aligned}
avatar
文章
阅读
粉丝