机器学习—隐马尔科夫模型(5)后向传播

持续创作，加速成长！这是我参与「掘金日新计划 · 6 月更文挑战」的第8天，点击查看活动详情

在这篇文章需要做哪些准备

• 隐马尔可夫模型
• 隐马尔可夫性质
• 条件独立
• 联合概率乘法
• 边缘概率

后向概率

有了前向概率基础，可能后向概率对于我们理解应该不难。首先先把后向概率表示写出来如下，也就是后向概率是给定当前时刻隐含状态确定为某一个状态的条件下，随后到从 $t+1$ 时刻到 $T$ 时刻观测值组成的观测序列的概率。

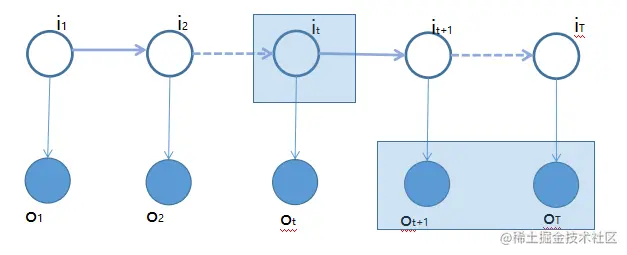
在上图中，用浅蓝色区域为 $\beta_t(i)$ 表示，只不过这里 $i$ 表示在 $t$ 时刻状态是确定为 $q_i$ 状态的条件下出现序列 $o_{t+1},\cdots,o_T$ 的概率。

是从 t 时刻一路向前推，也就是从后向前推可以得到 $\beta_1$ 来计算，这个基本思路预

上面的式子就是在 $t$ 时刻，状态为 $q_i$ 的后向概率表达式，也就是找到可以将问题子问题化的公式这一步比较重要。

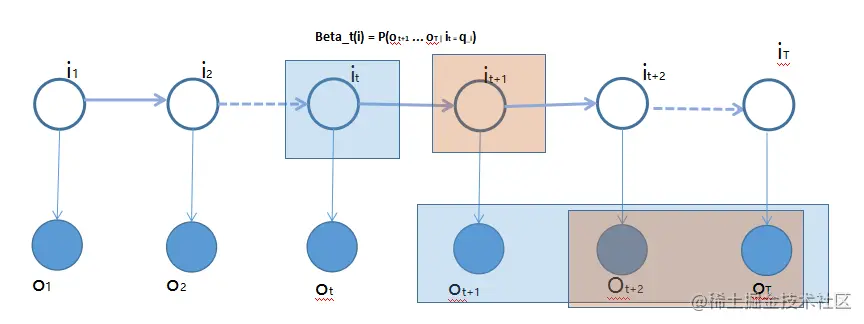
基本思想

基本思想也是 DP(动态规划)问题，既然是 DP 问题，那么重要是找到递归式以及退出递归的条件，接下来我们就从这两个方面入手，首先来看到退出递归的条件也就是从

可以通过后一个时刻 $t+1$ 来计算 $t$ 时刻的后向概率，这样一路回溯到 $t_1$ 时刻，也就是从 $t_T$ 时刻到 $t_1$ 时刻后向概率来计算出 $P(O|\lambda)$

上面公式是根据后向概率，来得出 $\beta_1(i)$ 也就是在给定了 $i_1=q_i$ (表示在 1 时刻状态为 $q_i$)条件出现 $o_2,\cdots, o_T$ 观测值组成观测序列的概率。

然后我们需要根据在 $t_1$ 时刻的 $\beta_1(i)$ 来计算 $P(O|\lambda)$

接下来我们需要在上面公式上通过利用边缘概率引入 $i_1=q_i$，

然后就是可以利用联合概率的乘法公式

这里 $P(i_1=q_i) = \pi_i$ 所以上面式子进过带换可以得到下面式子

继续对于 $o_1,\cdots,o_T$ 应用联合概率的乘法公式表示为 $P(o_1| o_2,\cdots,o_T,i_1 = q_i)P(o_2,\cdots,o_T|i_1=q_i)$

• $P(o_1| o_2,\cdots,o_T,i_1 = q_i)$ 可以利用观测独立假设，可以得到 $P(o_1|i_1=q_i)$
• 观测 $P(o_2,\cdots,o_T|i_1=q_i)$ 不难看出这就是在 $t_1$ 时刻的后向概率，所以可以替换为 $\beta_1(i)$

好了到这里我们就完成

递推公式

接下来我们就需要在 $t$ 时刻和 $t+1$ 时刻之间建立关系，$\beta_t(i)$ 和 $\beta_{t+1}(j)$ 之间

然后还是之前套路，将 $t+1$ 时刻状态引入进来 $i_{t+1} = q_j$ 如下

接下来利用联合概率乘法公式，将 $P(o_{t+1},\cdots,o_T,i_{t+1}=q_j|i_t=q_i)$ 进一步分解为 $P(o_{t+1},\cdots,o_T|i_{t+1}=q_j,i_t=q_i)P(i_{t+1}=q_j|i_t=q_i)$

先列出 t 时刻后向概率时刻，在上面公式中 $P(i_{t+1}=q_j|i_t=q_i)$ 不就是 $a_{ij}$

我们 $P(i_{t+1}=q_j|i_t=q_i)$

这一步我们可以通过条件独立假设来解释一下，因为 $i_{t+1}=q_j$ 观测到条件下，$o_{t+1},\cdots,o_T$ 只与 $i_{t+1}=q_j$ 相关，所以可以 $P(o_{t+1},\cdots,o_T|i_{t+1}=q_j,i_t=q_i) = P(o_{t+1},\cdots,o_T|i_{t+1}=q_j)$

这样一路推到,我们就在 $\beta_t(i)$ 和 $\beta_{t+1}(j)$ 之间建立了关系。