机器学习—隐马尔科夫模型(4) 前向概率方法

持续创作，加速成长！这是我参与「掘金日新计划 · 6 月更文挑战」的第6天，点击查看活动详情

在机器学习中，许多算法在开始都似懂非懂，其实有些经验想给想要入门机器学习，底座比较薄弱的朋友，本人就是一个离开校园多年，因为自己学校一般，许多在机器学习中用到知识点在学校时候都没见过，所以学习起来有些吃力，而且不是一般吃力。不过这不是我想说的重点，重点面对困难，最后方法就是反复，同一个知识点反复看几遍，其实每一遍都有新的体会和收获。

这一次分享我们继续上一次分享，所以请先阅读 机器学习—隐马尔科夫模型(3) 前向概率方法

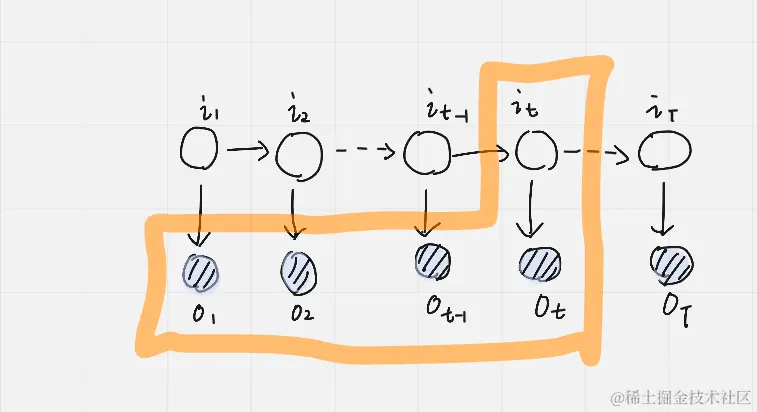
我们简单回归一下上一次分享内容，在上一次分享中，最后留下的问题是我们要找到 $\alpha_{t+1}(j)$ 与上一个时刻 $\alpha_{t}(i)$ 这两个前向概率之间的关系，首先需要列出 $\alpha_{t+1}(j)$ 公式如下:

然后还是利用边缘概率的性质引入 $i_t=q_i$，引入的目标也只是为构建出一个 $\alpha_t(i)$ 形式，通常引入一个随机变量的方式，都是将其引入后在对其求和(离散)或者积分(连续)。

接下来就是用联合概率乘积形式可以表示如下形式

然后就需要更好利用隐马尔科夫的观测条件独立假设和齐次 markov 性质，其中 $P(o_{t+1}|o_1,\cdots o_t,i_{t+1}=q_j,i_t=q_i|\lambda)$ 可以利用观测独立条件化简为 $P(o_{t+1}|i_{t+1}=q_j)$

然后需要对 $P(o_1,\cdots,o_t,i_t=q_i,i_{t+1}=q_j|\lambda)$ 进一步化简来得到如下的式子

$P(i_{t+1}=q_j|o_1,\cdots,i_t=q_i,\lambda)$ 可以齐次 markov 假设化简为 $P(i_{t+1}=q_j|i_t=q_i,\lambda)$ 然后再去看 $P(o_1,\cdots,o_t,i_t=q_i|\lambda)$ 也就是 $\alpha_t(i)$ 这样就建立了 $\alpha_{t+1}(j)$ 和 $\alpha_t(i)$ 之间的关系。

这样就建立了关系，这样就可以一步一步求出 $\sum_{i=1}^N \alpha_T(i)$ ,通常上面推导过程不难看出，当想要引入一个随机变量时候，就可以利用边缘概率来引入变量，还可以 markov 的两个性质对程序的化简。