知识蒸馏中的温度参数（2）1、温度常数简介由上一篇我所写知识蒸馏中的温度参数(1)中我介绍了知识蒸馏以及具体的损失

1、温度常数简介

由上一篇我所写知识蒸馏中的温度参数(1)中我介绍了知识蒸馏以及具体的损失函数的表达式。其中损失函数中：
其中L_soft中就涉及到了常数T，而T有应该设置为多少会比较合适呢？它与模型训练又有哪些具体的联系呢？

2、温度常数设定

2.1 温度常数的特性

当 T = 1 时，那即与普通的softmax一致
当 T > 1 时，softmax后的值就会分布的更加均匀，平缓
当 T < 1 时，softmax取值后会变得更加陡峭

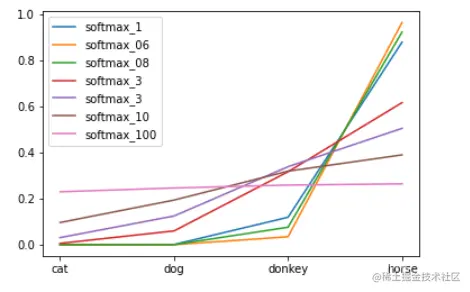
以上图片来自于：知识蒸馏(knowledge distillation)测试以及利用可学习参数辅助知识蒸馏训练Student模型

结论：当T值比较大时，因为各个值都会变得平均，负标签显著变大，此时学生模型对于负标签的关注度也会增大。反之，当T值较小时，负标签会变得更小，学生模型对于负标签的关注也会减少。

所以总结一下：

从有部分信息量的负标签中学习 --> 温度要高一些
防止受负标签中噪声的影响 --> 温度要低一些

还有一种说法是：Student_Net的参数量小时，因为不能捕获所有Teacher_Net的知识，可以选择适当忽略掉某些负标签，选择一个温度常数较低的值（没有试验过，待考证）

3、讨论

既然Student_Net学习了Teacher_Net输出的logit，为何不用学生模型的logit直接拟合Teacher_Net的logit呢？即直接用两者的平方差公式。

$\qquad\qquad \qquad Loss_{diff} = 1/2 * \sum\limits_1^N(v_i - u_i)^2 \qquad\qquad(1)$

这里提出了一个观点：当 $T \rightarrow \infty$ 时，优化L_soft就等价于平方差公式。
具体公式推导如下：

$\qquad \qquad \qquad \frac{\partial L_{soft}}{\partial u_i} = \frac{1}{T}(q_i-p_i) = \frac{1}{T}(\frac{\mathrm{e^{u_i/T}}}{\sum\limits_1^N{\mathrm{e}^{u_{j/T}}}} - \frac{\mathrm{e^{v_i/T}}}{\sum\limits_1^N{\mathrm{e}^{v_{j/T}}}})\qquad(2)$

根据洛必达法则, 当 $x\rightarrow0, 则有\mathrm{e}^x -1 \rightarrow x$ 。
当 $T \rightarrow \infty，u_i/T \rightarrow 0, 可得到\quad\mathrm{e}^{u_{j/T}} \rightarrow 1+u_j/T$
所以此时2式可以化简为：

$\qquad\qquad\qquad\frac{1}{T}(\frac{u_{i}/T + 1}{N+\sum u_i/T} - \frac{v_{i}/T + 1}{N+\sum v_i/T}) \qquad\qquad\qquad\qquad\qquad(3)$

由于模型输出一般会符合标准正态分布，所以假设 $\sum u_i = \sum v_i = 0$
所以3式会化简为
$\qquad\qquad\qquad\qquad\frac{\partial L_{sofft}}{\partial u_i} \approx\frac{1}{NT^2}(u_i-v_i)\qquad\qquad\qquad\qquad\quad(4)$

从上可以看到4式得到的偏导结果即是1式对u_i求偏导数结果一致。

结论：Loss_diff其实就是 $T\rightarrow \infty$ 的特殊情况

4、参考

# 知识蒸馏(knowledge distillation)测试以及利用可学习参数辅助知识蒸馏训练
 # 知识蒸馏(Knowledge Distillation) 经典之作
以上便是关于温度常数涉及到的知识点。因为本人水平有限，如若文中有错误，欢迎提出。