剑指 Offer 07. 重建二叉树持续创作，加速成长！这是我参与「掘金日新计划 · 6 月更文挑战」的第5天，点击查看

持续创作，加速成长！这是我参与「掘金日新计划 · 6 月更文挑战」的第5天，点击查看活动详情

剑指 Offer 06. 重建二叉树

Leetcode : leetcode-cn.com/problems/yo…

GitHub : github.com/nateshao/le…

题目描述：输入某二叉树的前序遍历和中序遍历的结果，请构建该二叉树并返回其根节点。

假设输入的前序遍历和中序遍历的结果中都不含重复的数字。

示例1：

Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]

示例 2:

Input: preorder = [-1], inorder = [-1]
Output: [-1]

限制：0 <= 节点个数 <= 5000

方法一：递归

//Definition for a binary tree node.
type TreeNode struct {
	Val   int
	Left  *TreeNode
	Right *TreeNode
}

func buildTree(preorder []int, inorder []int) *TreeNode {
    if len(preorder) == 0 {
        return nil
    }
    root := &TreeNode{preorder[0], nil, nil}
    i := 0
    for ; i < len(inorder); i++ {
        if inorder[i] == preorder[0] {
            break
        }
    }
    root.Left = buildTree(preorder[1:len(inorder[:i])+1], inorder[:i])
    root.Right = buildTree(preorder[len(inorder[:i])+1:], inorder[i+1:])
    return root
}

解题思路 ：

前序遍历性质：节点按照 [ 根节点 | 左子树 | 右子树 ] 排序。中序遍历性质：节点按照 [ 左子树 | 根节点 | 右子树 ] 排序。

以题目示例为例：

前序遍历划分 [ 3 | 9 | 20 15 7 ]

中序遍历划分 [ 9 | 3 | 15 20 7 ]

根据以上性质，可得出以下推论：

前序遍历的首元素为树的根节点 node 的值。
在中序遍历中搜索根节点 node 的索引，可将 中序遍历 划分为 [ 左子树 | 根节点 | 右子树 ] 。
根据中序遍历中的左（右）子树的节点数量，可将 前序遍历 划分为 [ 根节点 | 左子树 | 右子树 ] 。

通过以上三步，可确定三个节点 ：1.树的根节点、2.左子树根节点、3.右子树根节点。

根据「分治算法」思想，对于树的左、右子树，仍可复用以上方法划分子树的左右子树。

分治算法解析：

递推参数： 根节点在前序遍历的索引 root 、子树在中序遍历的左边界 left 、子树在中序遍历的右边界 right ；
终止条件： 当 left > right ，代表已经越过叶节点，此时返回 null ；
递推工作：
1. 建立根节点 node ：节点值为 preorder[root] ；
2. 划分左右子树：查找根节点在中序遍历 inorder 中的索引 i ；
  
  为了提升效率，本文使用哈希表 dic 存储中序遍历的值与索引的映射，查找操作的时间复杂度为O(1) ；
3. 构建左右子树：开启左右子树递归；

	根节点索引	中序遍历左边界	中序遍历右边界
左子树	`root + 1`	`left`	`i - 1`
右子树	`i - left + root + 1`	`i + 1`	`right`

TIPS： i - left + root + 1含义为根节点索引 + 左子树长度 + 1

返回值：回溯返回 node ，作为上一层递归中根节点的左 / 右子节点；

动图演示：

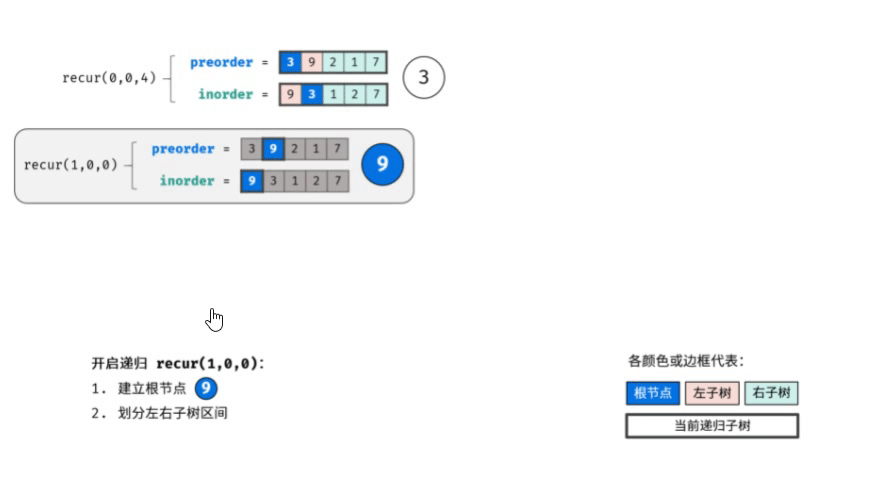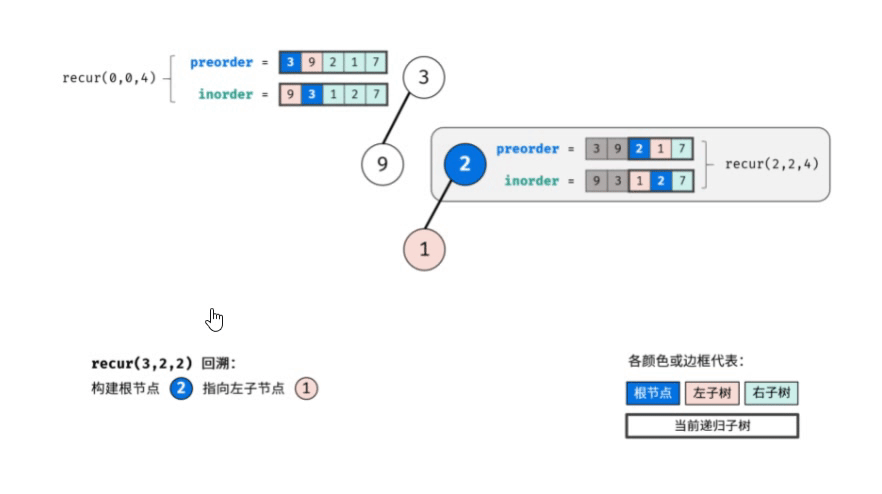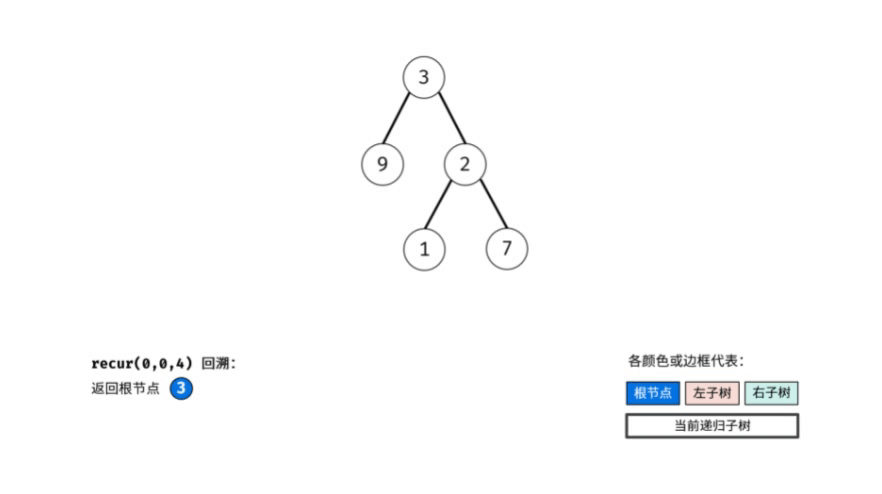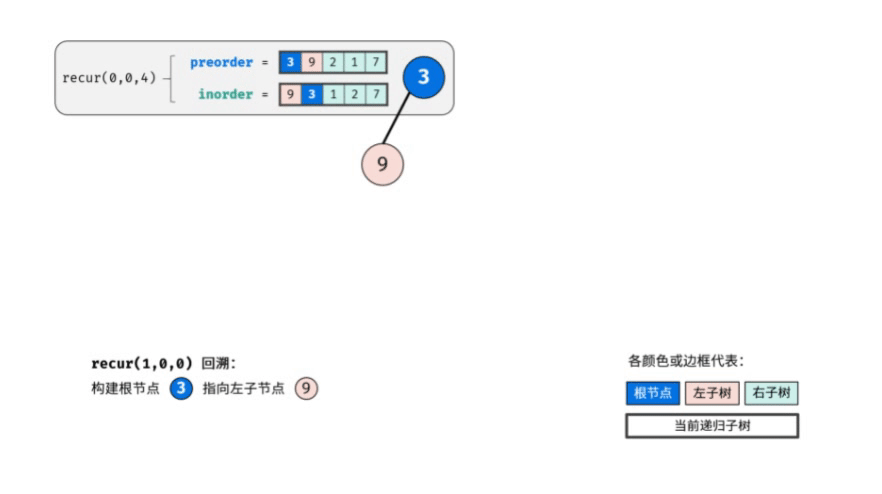
复杂度分析：

时间复杂度 O(N) ：其中 N 为树的节点数量。初始化 HashMap 需遍历 inorder ，占用 O(N) 。递归共建立 N 个节点，每层递归中的节点建立、搜索操作占用 O(1) ，因此使用 O(N) 时间。
空间复杂度 O(N) ： HashMap 使用 O(N) 额外空间；最差情况下（输入二叉树为链表时），递归深度达到 N ，占用 O(N) 的栈帧空间；因此总共使用 O(N) 空间。

package com.nateshao.sword_offer.topic_06_buildTree;

import java.util.Arrays;
import java.util.HashMap;
import java.util.Map;

/**
 * @date Created by 邵桐杰 on 2021/11/17 10:48
 * @微信公众号 程序员千羽
 * @个人网站 www.nateshao.cn
 * @博客 https://nateshao.gitee.io
 * @GitHub https://github.com/nateshao
 * @Gitee https://gitee.com/nateshao
 * Description: 重建二叉树 难度：中等
 */
public class Solution {
    public static void main(String[] args) {
        int[] preorder = {1, 2, 4, 7, 3, 5, 6, 8};
        int[] inorder = {4, 7, 2, 1, 5, 3, 8, 6};
    }
    /**
     * 思路：先找出根节点，然后利用递归方法构造二叉树
     * 代码实现：时间复杂度：O(n)，空间复杂度：O(n)
     * 解法一：递归（传入数组的拷贝）
     *
     * @param pre
     * @param in
     * @return
     */
    public TreeNode reConstructBinaryTree(int[] pre, int[] in) {
        if (pre == null || in == null || pre.length == 0 || in.length == 0) {
            return null;
        }
        if (pre.length != in.length) {
            return null;
        }
        TreeNode root = new TreeNode(pre[0]);
        for (int i = 0; i < pre.length; i++) {
            if (pre[0] == in[i]) {
                root.left = reConstructBinaryTree(Arrays.copyOfRange(pre, 1,
                        i + 1), Arrays.copyOfRange(in, 0, i));
                root.right = reConstructBinaryTree(Arrays.copyOfRange(pre,
                        i + 1, pre.length), Arrays.copyOfRange(in, i + 1, in.length));
            }
        }
        return root;
    }


//    HashMap<Integer, Integer> map = new HashMap<>();//标记中序遍历
//    int[] preorder;//保留的先序遍历，方便递归时依据索引查看先序遍历的值
//    public TreeNode buildTree(int[] preorder, int[] inorder) {
//        this.preorder = preorder;
//        //将中序遍历的值及索引放在map中，方便递归时获取左子树与右子树的数量及其根的索引
//        for (int i = 0; i < inorder.length; i++) {
//            map.put(inorder[i], i);
//        }
//        //三个索引分别为
//        //当前根的的索引
//        //递归树的左边界，即数组左边界
//        //递归树的右边界，即数组右边界
//        return recur(0, 0, inorder.length - 1);
//    }
//
//    TreeNode recur(int pre_root, int in_left, int in_right) {
//        if (in_left > in_right) return null;// 相等的话就是自己
//        TreeNode root = new TreeNode(preorder[pre_root]);//获取root节点
//        int idx = map.get(preorder[pre_root]);//获取在中序遍历中根节点所在索引，以方便获取左子树的数量
//        //左子树的根的索引为先序中的根节点+1
//        //递归左子树的左边界为原来的中序in_left
//        //递归左子树的右边界为中序中的根节点索引-1
//        root.left = recur(pre_root + 1, in_left, idx - 1);
//        //右子树的根的索引为先序中的 当前根位置 + 左子树的数量 + 1
//        //递归右子树的左边界为中序中当前根节点+1
//        //递归右子树的右边界为中序中原来右子树的边界
//        root.right = recur(pre_root + (idx - in_left) + 1, idx + 1, in_right);
//        return root;
//    }

    /**
     * 官方题解
     * 时间复杂度：O(n)，其中 nn 是树中的节点个数。
     *
     * 空间复杂度：O(n)，除去返回的答案需要的 O(n) 空间之外，
     * 我们还需要使用 O(n) 的空间存储哈希映射，以及 O(h)（其中 h 是树的高度）的空间表示递归时栈空间。
     * 这里 h < n，所以总空间复杂度为 O(n)。
     */
    private Map<Integer, Integer> indexMap;
    public TreeNode myBuildTree(int[] preorder, int[] inorder, int preorder_left, int preorder_right, int inorder_left, int inorder_right) {
        if (preorder_left > preorder_right) return null;

        // 前序遍历中的第一个节点就是根节点
        int preorder_root = preorder_left;
        // 在中序遍历中定位根节点
        int inorder_root = indexMap.get(preorder[preorder_root]);

        // 先把根节点建立出来
        TreeNode root = new TreeNode(preorder[preorder_root]);
        // 得到左子树中的节点数目
        int size_left_subtree = inorder_root - inorder_left;
        // 递归地构造左子树，并连接到根节点
        // 先序遍历中「从 左边界+1 开始的 size_left_subtree」个元素就对应了中序遍历中「从 左边界 开始到 根节点定位-1」的元素
        root.left = myBuildTree(preorder, inorder, preorder_left + 1, preorder_left + size_left_subtree, inorder_left, inorder_root - 1);
        // 递归地构造右子树，并连接到根节点
        // 先序遍历中「从 左边界+1+左子树节点数目 开始到 右边界」的元素就对应了中序遍历中「从 根节点定位+1 到 右边界」的元素
        root.right = myBuildTree(preorder, inorder, preorder_left + size_left_subtree + 1, preorder_right, inorder_root + 1, inorder_right);
        return root;
    }

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        int n = preorder.length;
        // 构造哈希映射，帮助我们快速定位根节点
        indexMap = new HashMap<Integer, Integer>();
        for (int i = 0; i < n; i++) {
            indexMap.put(inorder[i], i);
        }
        return myBuildTree(preorder, inorder, 0, n - 1, 0, n - 1);
    }


    public static class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;

        TreeNode(int x) {
            val = x;
        }
    }

方法二：迭代-栈

思路：找到根节点，左子树，右子树

我们用一个栈和一个指针辅助进行二叉树的构造。初始时栈中存放了根节点（前序遍历的第一个节点），指针指向中序遍历的第一个节点；
我们依次枚举前序遍历中除了第一个节点以外的每个节点。如果 index 恰好指向栈顶节点，那么我们不断地弹出栈顶节点并向右移动 index，并将当前节点作为最后一个弹出的节点的右儿子；如果 index 和栈顶节点不同，我们将当前节点作为栈顶节点的左儿子；
无论是哪一种情况，我们最后都将当前的节点入栈。

class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        if (preorder == null || preorder.length == 0) {
            return null;
        }
        TreeNode root = new TreeNode(preorder[0]);
        Deque<TreeNode> stack = new LinkedList<TreeNode>();
        stack.push(root);
        int inorderIndex = 0;
        for (int i = 1; i < preorder.length; i++) {
            int preorderVal = preorder[i];
            TreeNode node = stack.peek();
            if (node.val != inorder[inorderIndex]) {
                node.left = new TreeNode(preorderVal);
                stack.push(node.left);
            } else {
                while (!stack.isEmpty() && stack.peek().val == inorder[inorderIndex]) {
                    node = stack.pop();
                    inorderIndex++;
                }
                node.right = new TreeNode(preorderVal);
                stack.push(node.right);
            }
        }
        return root;
    }
}

func buildTree(preorder []int, inorder []int) *TreeNode {
    if len(preorder) == 0 {
        return nil
    }
    root := &TreeNode{preorder[0], nil, nil}
    stack := []*TreeNode{}
    stack = append(stack, root)
    var inorderIndex int
    for i := 1; i < len(preorder); i++ {
        preorderVal := preorder[i]
        node := stack[len(stack)-1]
        if node.Val != inorder[inorderIndex] {
            node.Left = &TreeNode{preorderVal, nil, nil}
            stack = append(stack, node.Left)
        } else {
            for len(stack) != 0 && stack[len(stack)-1].Val == inorder[inorderIndex] {
                node = stack[len(stack)-1]
                stack = stack[:len(stack)-1]
                inorderIndex++
            }
            node.Right = &TreeNode{preorderVal, nil, nil}
            stack = append(stack, node.Right)
        }
    }
    return root
}

链接：