机器学习—隐马尔科夫模型(3) 前向概率方法

持续创作，加速成长！这是我参与「掘金日新计划 · 6 月更文挑战」的第4天，点击查看活动详情

感觉很少有人能一次就把文章写得比较完整，所以自己也准备不断学习，然后推敲文字，争取以后把每一篇文章写得不说浅显易懂吧，希望对您了解这方面知识会有所帮助

概要

• 简单回顾一下 HMM 的数学模型
• 评估问题求解一般方法
• 为什么引入前向概率来求解 $P(O|\lambda)$
• 前向概率的推导

简单回顾

上一次分享简单总结一下前向算法，有点过于简单，这一次我们准备详细地推导一遍前向算法，在开始之前我们简单对 HMM 模型总结一下

隐马尔可夫模型中，是由隐含随机变量和观测随机变量组成时序模型，在每一个时刻 t 我们能够观测到的随机变量用 $O$ 来表示，这里 $O$ 表示一个随机变量集合，通常可以表示为 $Q = \{o_1,o_2,\cdots,o_T\}$ 那么每一个随机变量取值可能用集合 $V$ 记做 $V = \{v_1,v_2,\cdots, v_m\}$ 那么也就是观测随机变量可能是 m 个值，每一个观测值都是与对应时刻的隐含随机变量相关的，那么用大写字母 $I$ 表示隐含变量，记做 $I = \{i_1,i_2,\cdots,i_T\}$ ,每一个时刻隐含变量可能取值为 $Q$ 来表示也就是 $Q = \{q_1, q_2,\cdots,q_N\}$。

每一个时刻从某一个状态转移到另一个状态记做 $a_{ij} = P(i_{t+1}=q_j|i_t=q_i)$ 而某一个状态到观测值的概率为观测生成概率为 $b_j(k) = P(o_t=v_k|i_t=q_j)$ 这两个概率是状态转移概率 A 和观测生成概率 B。

然后我们再去总结 2 个假设，分别是齐次马尔科夫假设和

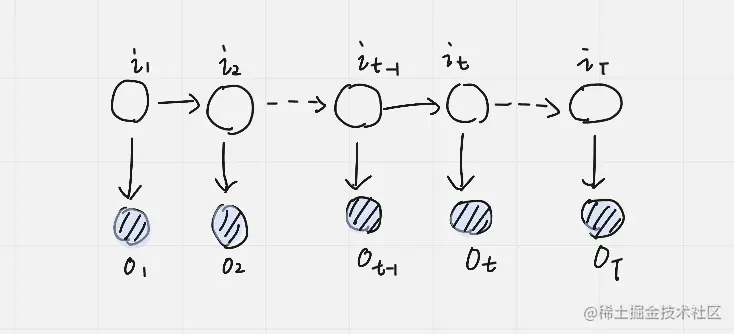
评估问题

我们要求解的是 $P(O|\lambda)$ 也就是在给定了参数 $\lambda$ 条件下，观测到 $O$ 的观测序列的概率是多少

然后可以通过引入隐含状态序列 $I$ ，引入后通过 I 求和也就是利用边缘概率性质可以将 $P(O|\lambda) = \sum_I P(I,O|\lambda)$ 接下来我们联合概率的乘法可以得到 $\sum_I P(I,O|\lambda) = \sum_I P(O|I,\lambda)P(I|\lambda)$。

然后我们先 $P(I|\lambda)$ 中 $I$ 序列进行展开

其中 $P(i_t|i_1,\cdots,i_{t-1},\lambda)$ 利用齐次马尔科夫性质可以得到 $P(i_t|i_{t-1})$, 也就是 $a_{i_{t-1},i_t}$ 这种写法，然后再看 $P(i_1,\cdots,i_{t-1}|\lambda)$ 不难看出递归的形式，所以可以递归下去

然后我们再去看 $P(O|I,\lambda)$ 这里推导过程和上面也比较类似

开始还是将其展开写成 $P(o_1,\cdots,o_t|i_1,\cdots,i_t,\lambda)$ 然后将联合概率写成条件概率

根据马尔科夫观测独立假设 $P(o_t|o_1,\cdots,o_{t-1},i_1,\cdots,i_t,\lambda)$ 可得到 $P(o_t|i_t) = b_{i_t}(o_t)$

然后继续将 $P(O|I,\lambda)$ 和 $P(I|\lambda)$ 带入到上面式子得到

这里 $\sum_I$ 表示 T 个 $i_t$ 求和符号，所以将 $\sum_I$ 展开来写成

可以将上面式子改写为

这样计算时间复杂度为 $O(N^T)$ 接下来我们来看一看如何将计算过程进行化简来得到,这是因为其计算时间复杂度问题，所以才引入前向概率算法

前向概率

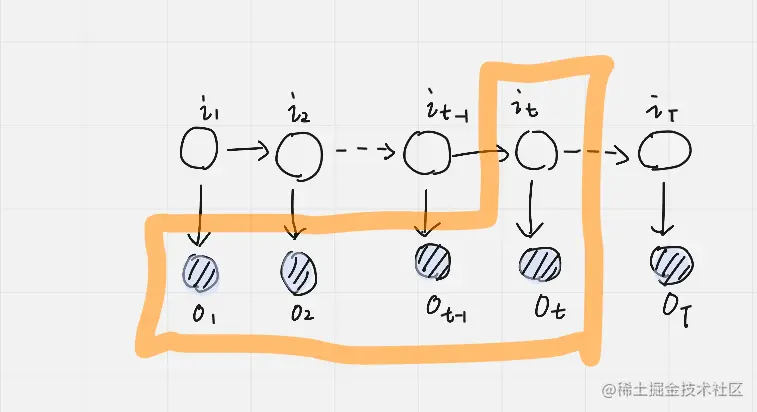
这里设计一个前向概率如上图，所谓前向概率就是对应某一个时刻，例如上图 t 时刻的联合概率用 $\alpha_t(i)$ 这里 t 表示时刻，而 i 表示 t 时刻状态为 $q_i$ 的联合概率值。

结合上面图中橘黄色部分的我们可将 $\alpha_t(i)$ 展开为 $\alpha_t(i) = P(o_1,\dots,o_t,i_t =q_i|\lambda)$，那么求解 $P(O|\lambda)$ 概率就会转为为求 T 时刻的前向概率问题

然后通过就是要找到 $\alpha_{t+1}(j)$ 与 $\alpha_t(i)$ 之间关系，只要能够找到一个等式中存在 $\alpha_{t+1}(j)$ 与 $\alpha_t(i)$ 我们就建立之间关系，由于这部分内容比较多，所以放到下一节给大家解释

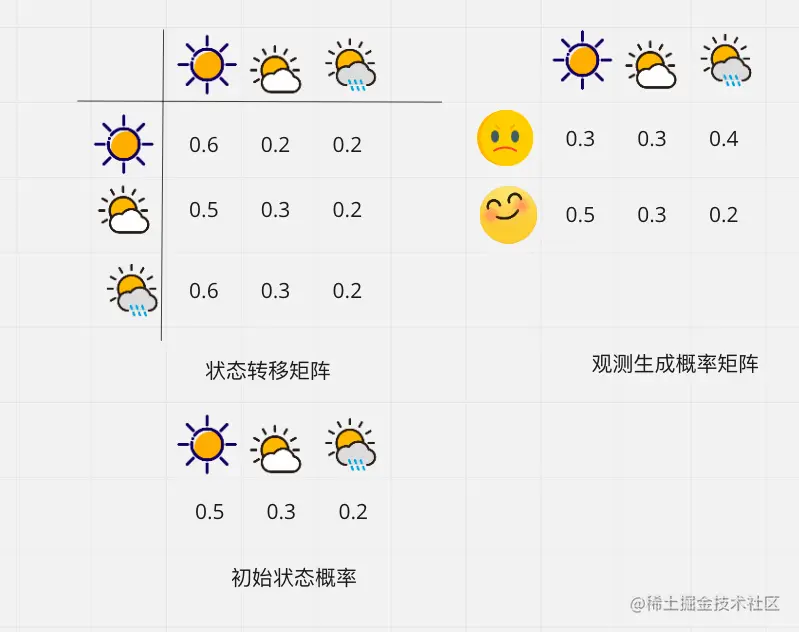
上面列出已知条件，也就是分别是$\pi$ 状态初始值概率分布，状态转移概率和观测生成概率矩阵

这是我们观察序列

为了便于计算我们将随机事件用数值来表示

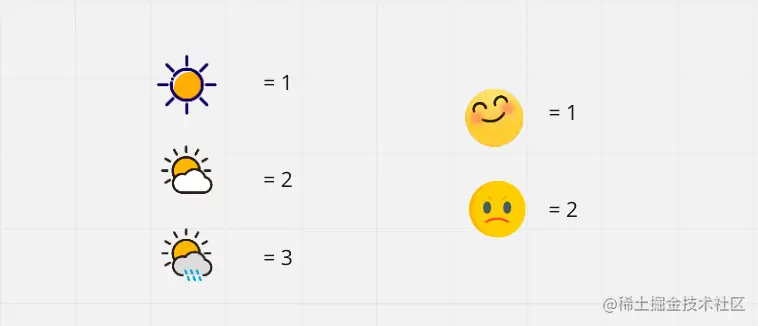
import numpy as np

pi_0 = np.array([0.5,0.3,0.2])

A = np.array([
   [0.6,0.2,0.2],
   [0.5,0.3,0.2],
   [0.6,0.2,0.2]
])

B = np.array([
   [0.5,0.3,0.2],
   [0.3,0.3,0.4]
])

# B_0 B_1 B_0

a_1 = pi_0 * B[0]
print(a_1)

a_1 = pi_0 * B[0]
print(a_1)

[0.25 0.09 0.04]

a_2 = np.dot(a_1,A)*B[1]
print(a_2)

[0.0657 0.0255 0.0304]

a_3 = np.dot(a_2,A)*B[0]
print(a_3)

[0.035205 0.008061 0.004864]

print(a_3.sum())