本文已参与「新人创作礼」活动，一起开启掘金创作之路。

0. 引言

作为一名算法工程师，在利用算法模型解决实际问题时，模型的欠拟合、过拟合问题是无论如何都无法回避的。这两个问题的表象相比很多人都知道，但是涉及到它们背后的产生原因、本质以及解决方法，要说清楚还是不容易的。

1. 误差、偏差和方差的数学定义

误差（error）的概念有两类，一类是数据本身带来的噪声，一般假设服从均值为0的高斯分布，记为 $\epsilon \sim N(0,\sigma_{\epsilon})$ (噪声的各变量是独立同分布于均值为0、方差为 $\sigma_{\epsilon}$ 的正态分布),且往往是认为无法避免的；另一类是模型输出与实际值之间的误差，例如均方误差（mean squared error, MSE),这个是实际应用中我们所直接关心的，一般希望它越小越好。假设现在有因变量 $y$ （输出）由自变量 $x$ （输入）决定，记真实的映射函数为 $f(x)$ (也叫真实的模型)，则

y=f(x)+\epsilon \tag{1-1}

对应的，记我们从数据中学习出的模型为 $\hat f(x)$ ,那么偏差（bias）的定义为：

Bias(\hat f(x))=E(\hat f(x))-f(x)\tag{1-2}

方差的定义为：

Var(\hat f(x))=E\left[\left(\hat f(x)-E(\hat f(x))\right)^2\right]\tag{1-3}

假设我们现在关心的是模型的均方误差 $MSE(\hat f(x)$ ，它的定义以及分解过程为：

\begin{aligned} MSE(\hat f(x))&=E\left[\left(y-\hat f(x)\right)^2\right]\\ &=E\left[\left(f(x)+\epsilon-\hat f(x)\right)^2\right]\\ &=E\left[\left(f(x)-\hat f(x)\right)^2+2\epsilon \left(f(x)-\hat f(x)\right)+\epsilon^2\right]\\ &=E\left[\left(f(x)-\hat f(x)\right)^2\right]+2E(\epsilon)E(f(x)-\hat f(x))+E(\epsilon^2)\\ &=E\left[\left(\left(f(x)-E(\hat f(x)\right)-\left(\hat f(x)-E(\hat f(x))\right)\right)^2\right]+0+\sigma_{\epsilon}^2\\ &=E\left[\left(f(x)-E(\hat f(x))\right)^2\right]-2E\left[\left(f(x)-E(\hat f(x))\right)\left(\hat f(x)-E(\hat f(x))\right)\right]+E\left[\left(\hat f(x)-E(\hat f(x))\right)^2\right]+\sigma_{\epsilon}^2\\ &=E(Bias(\hat f(x))^2)-2E\left[f(x)\hat f(x)-f(x)E(\hat f(x))-E(\hat f(x))\hat f(x)+E(\hat f(x))E(\hat f(x))\right]+Var(\hat f(x))+\sigma_{\epsilon}^2\\ &=Bias(\hat f(x))^2+Var(\hat f(x))+\sigma_{\epsilon}^2\\ \tag{1-4} \end{aligned}

注意，上述最后一步的化简中，用到了这些隐含条件（下面的常量是指关于数据的常量）：

$E(\hat f(x))$ 是常量， $f(x)$ 是常量，因 $此Bias(\hat f(x))$ 也是常量，且常量可以提到 $E()$ 外面去

由此可见，均方误差是取决于偏差、方差和随机误差的，且后三者的绝对值（平方）越大，均方误差也越大，这也符合我们的一般直觉。

2. 偏差与方差的直观理解

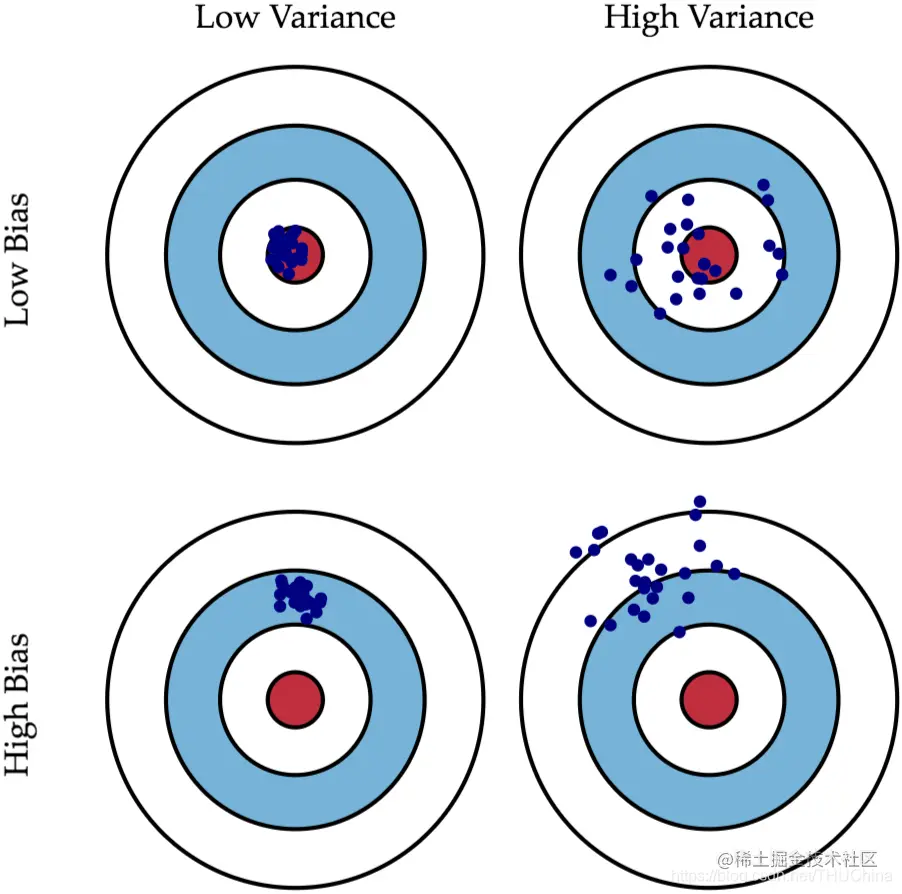
在这里插入图片描述

图2.1 偏差和方差的图形化解释

图片来源scott.fortmann-roe.com/docs/BiasVa… 如上图所示，对于某个靶子而言，上面的每个点表示给定算法的情况下，每次更换不同的训练样本训练出不同的模型，对同一个测试样本进行预测的结果。最理想的情况是左上角，此时偏差和方差都较小，因此模型的误差（例如前面提到的均方误差）较小；右上角是低偏差和高方差的情况，这体现出算法的输出结果不是很“稳定”，也即不同的数据训练出的模型，对同一样本的预测结果可能大相径庭；左下角是高偏差和低方差的情况，这体现出算法的输出结果虽然稳定但是与真实结果总存在一点偏差，类似于控制理论里面的静差；右下角是最糟糕的情况，偏差和方差都很大

3. 偏差、方差与欠拟合、过拟合的关系

结合上一章中的直观理解，偏差、方差与欠拟合、过拟合的关系其实呼之欲出了。

所谓欠拟合（underfitting），外在现象就是模型在训练集上和测试集上表现都不好。这就意味着，模型没有学习到数据中足够的信息，导致模型的输出与真实值存在较大偏差，也即高偏差。形象的比喻就是造狙击枪的车床有个明显的公差，导致造出来的狙击枪瞄准镜都往某个方向偏了一个角度，于是用这批狙击枪打靶都会网靶心某个方向偏移。

所谓过拟合（overfitting），外在现象就是模型在训练集上表现很好，但是在测试集上表现不好。这就意味着模型学习到了数据中的信息，但是学到的信息跟具体的训练数据强相关，缺乏举一反三、灵活变通的能力，导致模型的输出与真实值存在较大方差，也即高方差。形象的比喻就是学生只会背老师讲的题目模板，不论老师怎么教，只能记住老师教的那几个题。如果运气好，老师押中了考题，那么考得好；否则就考得差。

4. 欠拟合、欠拟合的产生原因及解决方案

前面讲到，出现欠拟合是因为模型没有学习到数据中的信息。造成这一结果的原因有：

模型复杂度不够，具体来说就是特征项不够。例如男女性别分类时，只有身高这一维特征。
正则化参数太大，导致将某些重要特征给抑制住了

对应的解决方法有：

添加输入特征，例如男女性别分类时，引入体重、头发长度等特征。
当输入数据的原始特征无法改变的时候，提高模型的特征抽取能力，“制造”出更丰富、有效的特征。例如引入多项式特征、卷积层、transformer结构等
减小正则化参数

过拟合是因为模型泛化能力太差，具体原因有：

输入特征过多，导致模型容易过拟合到某些特征上面，缺乏全局视野
模型结构过于复杂，导致提取出了过多的特征
训练数据不够多，没有覆盖完整测试集数据的分布空间
训练集中噪声过大，导致模型学到了许多无用信息

对应的解决方法：

进行特征筛选，减少输入特征数量
控制模型复杂度，避免选用过于复杂的模型解决相对简单的问题
在损失函数中引入L1/L2正则化，以减少某些不那么重要的特征的权重
增大训练数据集，尤其是提高训练集的分布丰富度
对训练数据进行数据增强，本质上和上一个方法是同样的效果
对数据进行清洗，剔除异常点
引入dropout，训练过程的一个技巧，某种程度上类似于正则化
early stop，某种程度上类似于正则化

通俗理解误差、偏差、方差以及它们和过拟合、欠拟合之间的关系.

0. 引言

1. 误差、偏差和方差的数学定义

2. 偏差与方差的直观理解

3. 偏差、方差与欠拟合、过拟合的关系

4. 欠拟合、欠拟合的产生原因及解决方案