凸优化理论基础3——凸集和凸锥重要例子

秃头小苏
1,078 阅读3分钟

🍊作者简介：秃头小苏，致力于用最通俗的语言描述问题

🍊往期回顾：凸优化理论基础1--仿射集    凸优化理论基础2——凸集和锥

🍊近期目标：拥有5000粉丝

🍊支持小苏：点赞👍🏼、收藏⭐、留言📩

 

凸优化理论基础3——超平面和半空间

  之前我们已经介绍了仿射集、凸集、凸锥等概念，这节将来介绍超平面和半空间。🌵🌵🌵

 

超平面

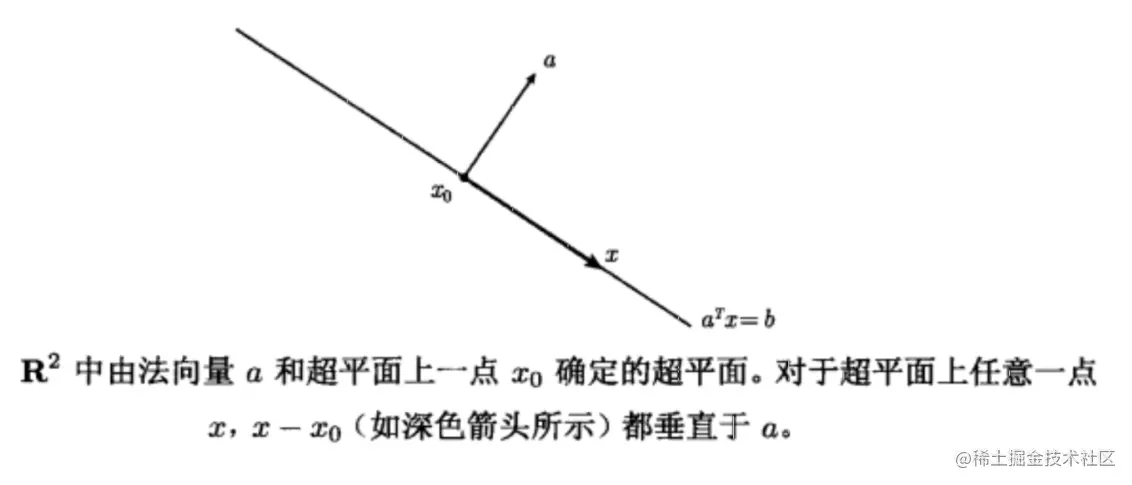
  定义： 超平面是具有下面形式的集合

{x∣aTx=b} ,a∈Rn,a≠0且b∈R\{x|a^Tx=b\} \ , \quad a \in R^n,a\ne 0且b \in R

  上述定义还可以表示成以下形式：

{x∣aT(x−x0)=0}\{x|a^T(x-x_0)=0\}

  其中x0x_0是超平面上的任意一点。不清楚观此视频🍜🍜🍜这里来看看超平面的几何解释，如下：

image-20220502102904090

 

半空间

  定义：半空间是具有下列形式的集合：

{x∣aTx≤b},a≠0\{x|a^Tx \le b\}, \quad a \ne 0

    一个超平面将RnR^n 划分为两个半空间。对于R2R^2来说，由aTx≥ba^Tx \ge b决定的半空间（无阴影部分）是向aa扩展的半空间；由aTx≤ba^Tx \le b决定的半空间（有阴影部分）是向−a-a扩展的半空间。向量aa 是这个半空间向外的法向量。

image-20220502103714090

   

超平面和半空间是凸集

​  首先直接给出以下结论：

  • 超平面是仿射集
  • 超平面是凸集
  • 半空间不是仿射集
  • 半空间是凸集

这里我想来证明证明超平面是凸集和半空间是凸集这两个结论【证明凸集及后面证明凸函数比较重要】

  1. 证明超平面是凸集

<img src="https://gitee.com/wsj-create/cloudimage/raw/master/img/image-20220502105954346.png" alt="image-20220502105954346" />

 

  1. 证明半空间是凸集

在这里插入图片描述

   

球和椭球

​  球的定义给出了三种方式，如下：

  1. B(xc,r)={x∣ ∣∣x−xc∣∣2}≤rB(x_c,r)=\{x| \ ||x-x_c||_2\} \le r 。其中r>0,∣∣⋅∣∣2r > 0,|| \cdot ||_2 表示二范数，向量xcx_c是球心，标量rr为半径。B(xc,r)B(x_c,r) 由距离不超过rr 的所有点组成 🍚🍚🍚
  2. B(xc,r)={x∣ (x−xc)T(x−xc)}≤r2B(x_c,r)=\{x | \ (x-x_c)^T(x-x_c)\} \le r^2
  3. B(xc,r)={xc+ru ∣ ∣∣u∣∣2≤1}B(x_c,r)=\{x_c+ru \ | \ ||u||_2 \le 1\}

球也是凸集，证明如下：【证明用到了二范数的齐次性及三角不等式】

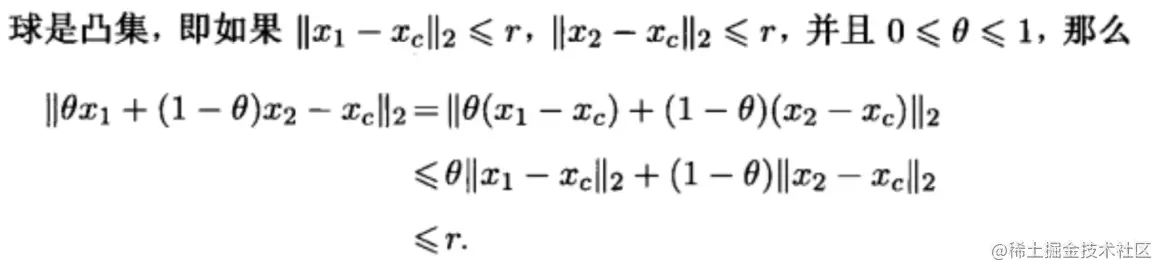
image-20220502150002153

椭球也是凸集，其定义如下：

ε={x∣ (x−xc)TP−1(x−xc)≤1}\varepsilon =\{x | \ (x-x_c)^TP^{-1}(x-x_c) \le 1 \}

其中P是对称正定矩阵。  

关于此部分视频链接：www.bilibili.com/video/BV1xp…🍁🍁🍁

   

范数球和范数锥

​  上面的球是针对二范数而言的，这里的范数球和范数锥类似于球的定义，不过不再限定二范数。

范数球定义：C={x∣ ∣∣x−xc∣∣≤r}C=\{x| \ ||x-x_c|| \le r \}

范数锥定义：C={(x,t)∣ ∣∣x∣∣≤t}C=\{ (x,t) | \ ||x|| \le t \}  

关于此部分视频链接：www.bilibili.com/video/BV1oA…🍁🍁🍁

    

多面体

  多面体被定义为有限个线性等式和不等式的解集，如下：

P={x∣ ajTx≤bj ,j=1 ,⋯ ,m , cjT=dj , j=1 ,⋯ , p}P=\{x | \ a^T_jx \le b_j \ ,j=1 \ , \cdots \ ,m \ , \ c^T_j=d_j \ , \ j=1 \ , \cdots, \ p\}

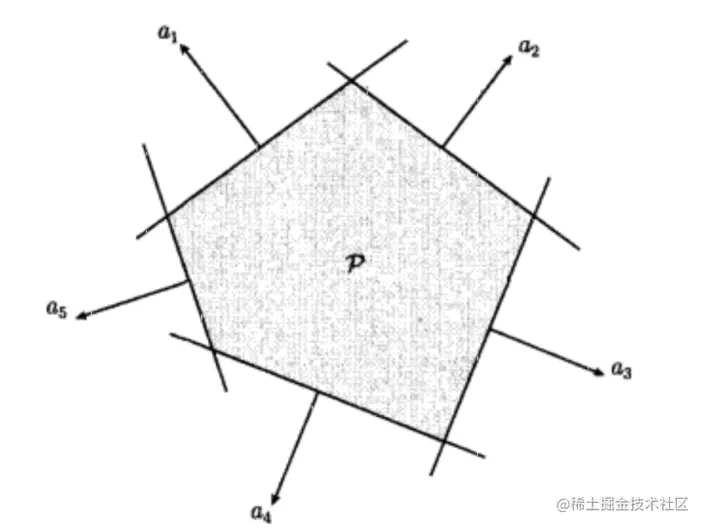
​  由定义可以看出，多面体是有限个半空间和超平面的交集。仿射集（如子空间、超平面、直线）、射线、线段和半空间都是多面体，且多面体是凸集。下图中的多面体由五个半空间的交集构成：

image-20220502155705718

   

单纯形

​  单纯形是一类重要的多面体。设k+1k+1个点v0,⋯ ,vk∈Rnv_0, \cdots ,v_k \in R^n仿射独立，即v1−v0,⋯ ,vk−v0v_1-v_0, \cdots ,v_k-v_0线性独立，那么这些点决定了一个单纯形，如下：

C=conv{v0,⋯ ,vk}={θ0v0+⋯+θkvk ∣ θ⪰0, 1Tθ=1}C=conv\{v_0, \cdots ,v_k \}=\{ \theta_0v_0+ \cdots +\theta_kv_k \ | \ \theta \succeq 0, \ 1^T \theta=1 \}

  其中1表示所有分量均为一的向量。这个单纯形的仿射维数为k，因此也称为RnR^n 空间的k维单纯形。

  下面给出一些常见的单纯形：

  • 一维单纯形是一条线段
  • 二维单纯形是一个三角形
  • 三维单纯形是一个四面体

   

半正定锥

数学符号SnS^nS+nS^n_+S++nS^n_{++}
中文名称对称矩阵对称半正定矩阵对称正定矩阵
数学表达式Sn={X∈Rn×n∥ X=XT}S^n=\{X \in R^{n\times n} \| \ X=X^T\}S+n={X∈Sn∥ X⪰0}S^n_+=\{X \in S^n \| \ X \succeq 0 \}S+n={X∈Sn∥ X≻0}S^n_+=\{X \in S^n \|\ X \succ 0 \}
是否为凸集✅✅✅
是否为凸锥✅✅❎

此部分参考视频：www.bilibili.com/video/BV1Gt…🍁🍁🍁

    如若文章对你有所帮助，那就🛴🛴🛴

咻咻咻咻~~duang~~点个赞呗

avatar
文章
阅读
粉丝