集成学习之梯度提升树（GBDT）原理详解

lankuohsing
717 阅读3分钟

本文已参与「新人创作礼」活动，一起开启掘金创作之路。

1. 梯度提升（Gradient Boosting）的思想

Gradient Boosting和Adaptive Boosting都属于boosting类集成学习算法，也即通过多轮迭代得到多个基学习器，然后将多个基学习器加权求和。

fm(x)=fm−1(x)+ρmhm(x)(1-1)f_m(x)=f_{m-1}(x)+\rho_mh_m(x)\tag{1-1}

不同之处在于，Adaptive Boosting在某次迭代过程中训练该轮基学习器时，会增大上一轮犯错样本的权重；而Gradient Boosting在某次迭代时，会拟合上一轮基学习器的负梯度。 为什么拟合上一轮的负梯度能work？我们知道机器学习中最小化损失函数L(θ)L(\theta)时，往往会利用梯度下降法来更新θ\theta：

θ=θ−α⋅∂L(θ)∂θ(1-2)\theta=\theta-\alpha\cdot \frac{\partial L(\theta)}{\partial \theta}\tag{1-2}

如果把θ\theta换成基学习器fm(x)f_m(x)，上述表达式也是可以用来更新基学习器的（具体的严格证明需要用到泛函分析的理论）:

fm(x)=fm−1(x)−ρm⋅∂L(y,fm−1(x))∂fm−1(x)(1-3)f_m(x)=f_{m-1}(x)-\rho_m\cdot \frac{\partial L(y,f_{m-1}(x))}{\partial f_{m-1}(x)}\tag{1-3}

其中L(y,fm−1(x))=∑i=1NL(yi,fm−1(xi))L(y,f_{m-1}(x))=\sum_{i=1}^NL(y_i,f_{m-1}(x_i)) {1−3}\{1-3\}意味着，我们是用第m轮的基学习器hm(x)h_m(x)去拟合上一轮损失函数关于fm−1(x)f_{m-1}(x)的负梯度，从而达到通过梯度下降法最小化L(f)L(f).该方法也叫函数空间的梯度下降法。

2. gradient boosting的通用算法流程

这里我们暂时不关心基学习器的具体表达式，把GBDT的通用算法流程列下来：

  1. 初始化:f0(x)=arg⁡min⁡γ∑i=1NL(yi,γ)f_0(x)=\arg \min\limits_{\gamma}\sum_{i=1}^NL(y_i,\gamma)
  2. for m=1 to M: (a)计算函数空间负梯度：yi~=∂L(yi,fm−1(xi))∂fm−1(xi),i=1,⋯ ,N\tilde{y_i}=\frac{\partial L(y_i,f_{m-1}(x_i))}{\partial f_{m-1}(x_i)}, i=1,\cdots,N (b)通过最小化平方误差，来得到hm(x)h_m(x)：wm=arg⁡min⁡w∑i=1N(yi~−hm(xi;w))2w_m=\arg\min\limits_{w}\sum_{i=1}{N}(\tilde{y_i}-h_m(x_i;w))^2 (c)使用line search确定系数ρm\rho_m:ρm=arg⁡min⁡ρ∑i=1NL(yi,fm−1(xi)+ρhm(xi;wm))\rho_m=\arg\min\limits{\rho}\sum_{i=1}^NL(y_i,f_{m-1}(x_i)+\rho h_m(x_i;w_m)) (d)更新基学习器：fm(x)=fm−1+ρmhm(x;wm)f_m(x)=f_{m-1}+\rho_m h_m(x;w_m)
  3. 输出最终的fM(x)f_M(x)

3. 将回归树作为基学习器，得到GBDT算法

3.1. 回归树介绍

在GBDT中，基学习器是决策树。因为基学习器要拟合的是负梯度，可以认为是个回归问题，因此我们来介绍一些回归树的基本概念。 决策树本质上可以看做一个分段函数，把特征空间分为多个互相独立的子区域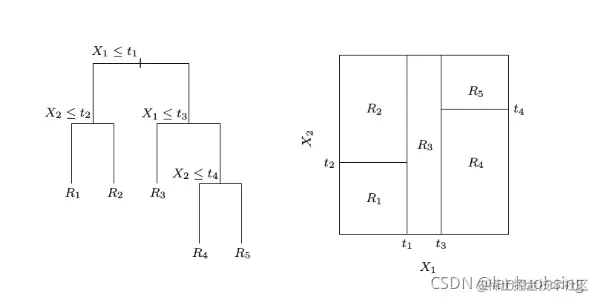： 在这里插入图片描述 图片来源www.cnblogs.com/massquantit… 因此单棵决策树在数学上可以表示为

h(x;{Rj,bj}1J=∑j=1JbjI(x∈Rj)(3-1)h(x;\{R_j,b_j\}_1^J=\sum_{j=1}^Jb_jI(x\in R_j)\tag{3-1}

其中{Rj}1J\{R_j\}_1^J代表决策树划分出的JJ个子空间（每个子空间对应一个叶结点），{bj}1J\{b_j\}_1^J代表各个子空间输出的值。

3.2. 将回归树应用到gradient boosting中

因此第2章里面的2.(b)可以写成：

{Rjm}1J=arg⁡min⁡{Rjm}1J∑i=1N(yi~−hm(xi;{Rjm,bjm}1J))2(3-2)\{R_{jm}\}_1^J=\arg\min\limits_{\{R_{jm}\}_1^J}\sum_{i=1}{N}(\tilde{y_i}-h_m(x_i;\{R_{jm},b_{jm}\}_1^J))^2\tag{3-2}

对应的bjm=meanx∈Rjm yi~b_{jm}=\mathop{mean}\limits_{x\in R_{jm}}\ \tilde{y_i}是该区域的平均值。（之所以可以先划分区域再求b，是因为不论怎么划分区域，b取该区域内所有值的平均值，总能最小化均方误差，因此可以先后求） 注意到2.(c)中求出的ρm\rho_m对于所有子区域是一样的，这样不一定是最优的，因此可以采用如下方式优化求取最优的γjm=ρjmbjm\gamma_{jm}=\rho_{jm}b_{jm}：

γjm=arg⁡min⁡γ∑xi∈RjmL(yi,fm−1(xi)+γ)(3-3)\gamma_{jm}=\arg\min\limits_{\gamma}\sum_{x_i\in R_{jm}}L(y_i,f_{m-1}(x_i)+\gamma) \tag{3-3}

3.3. GBDT算法流程

最终得到GBDT的算法流程：

  1. 初始化:f0(x)=arg⁡min⁡γ∑i=1NL(yi,γ)f_0(x)=\arg \min\limits_{\gamma}\sum_{i=1}^NL(y_i,\gamma)
  2. for m=1 to M: (a)计算函数空间负梯度：yi~=∂L(yi,fm−1(xi))∂fm−1(xi),i=1,⋯ ,N\tilde{y_i}=\frac{\partial L(y_i,f_{m-1}(x_i))}{\partial f_{m-1}(x_i)}, i=1,\cdots,N (b)通过最小化平方误差，来得到子区域划分方式（也即得到最终的决策树）：{Rjm}1J=arg⁡min⁡{Rjm}1J∑i=1N(yi~−hm(xi;{Rjm,bjm}1J))2\{R_{jm}\}_1^J=\arg\min\limits_{\{R_{jm}\}_1^J}\sum_{i=1}{N}(\tilde{y_i}-h_m(x_i;\{R_{jm},b_{jm}\}_1^J))^2 (c)使用line search确定子区域最终输出：γjm=arg⁡min⁡γ∑xi∈RjmL(yi,fm−1(xi)+γ)\gamma_{jm}=\arg\min\limits_{\gamma}\sum_{x_i\in R_{jm}}L(y_i,f_{m-1}(x_i)+\gamma) (d)更新基学习器：fm(x)=fm−1+∑j=1JγjmI(x∈Rjm)f_m(x)=f_{m-1}+\sum_{j=1}^J\gamma_{jm}I(x\in R_{jm})
  3. 输出最终的fM(x)f_M(x)

参考 www.cnblogs.com/massquantit…

avatar
文章
阅读
粉丝