持续创作，加速成长！这是我参与「掘金日新计划 · 6 月更文挑战」的第2天，点击查看活动详情

先认识什么是数据结构与算法

1.1 什么是数据结构

官方统一定义—— 没有……
“数据结构是数据对象，以及存在于该对象的实例和组成实例的数据元素之间的各种联系。这些联系可以通过定义相关的函数来给出。”
Sartaj Sahni，《数据结构、算法与应用》“数据结构是ADT（抽象数据类型 Abstract DataType）的物理实现。”
Clifford A.Shaffer，《数据结构与算法分析》“数据结构（data structure）是计算机中存储、组织数据的方式。通常情况下，精心选择的数据结构可以带来最优效率的算法。”

例题：写程序实现一个函数PrintN，使得传入一个正整数为N的参数后，能顺序打印从1到N的全部正整数。循环实现与递归实现

解决问题方法的效率，跟空间的利用效率有关。

所以到底什么是数据结构？？？

数据对象在计算机中的组织方式

逻辑结构
物理存储结构
数据对象必定与一系列加在其上的操作相关联
完成这些操作所用的方法就是算法

抽象数据类型（Abstract Data Type）

数据类型
数据对象集
数据集合相关联的操作集
抽象：描述数据类型的方法不依赖于具体实现
与存放数据的机器无关
与数据存储的物理结构无关
与实现操作的算法和编程语言均无关只描述数据对象集和相关操作集，“是什么”，并不涉及“如何做到”的问题。

1.2 什么是算法

算法（Algorithm）

一个有限指令集
接受一些输入（有些情况下不需要输入）
产生输出
一定在有限步骤之后终止
每一条指令必须
- 有充分明确的目标，不可以有歧义
- 计算机能处理的范围之内
- 描述应不依赖于任何一种计算机语言以及具体的实现手段

例1：选择排序算法的伪码描述


void SelectionSort ( int List[], int N )
{ 
  	/* 将N个整数List[0]...List[N-1]进行非递减排序 */
	for ( i = 0; i < N; i ++ ) {
	MinPosition = ScanForMin( List, i, N–1 );
	/* 从List[i]到List[N–1]中找最小元，并将其位置赋给MinPosition */
	Swap( List[i], List[MinPosition] );
	/* 将未排序部分的最小元换到有序部分的最后位置 */
	}
}

什么是好的算法？

空间复杂度S(n) —— 根据算法写成的程序在执行时占用存储单元的长度。这个长度往往与输入数据的规模有关。空间复杂度过高的算法可能导致使用的内存超限，造成程序非正常中断。
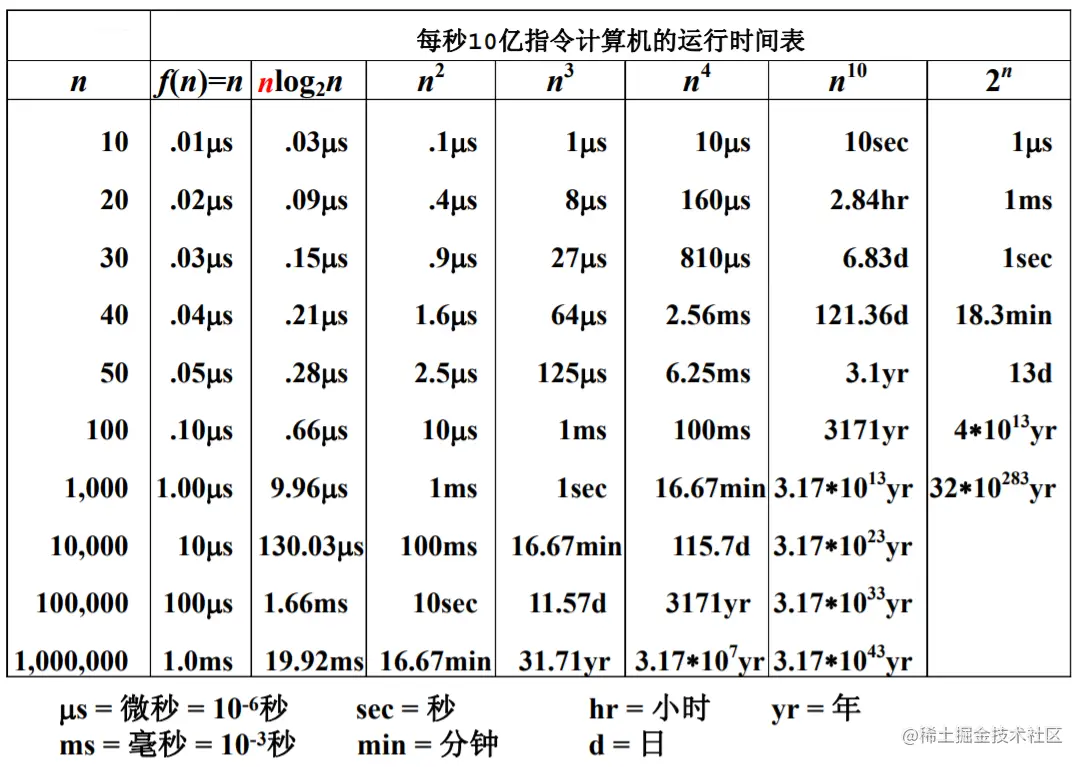
时间复杂度T(n)—— 根据算法写成的程序在执行时耗费时间的长度。这个长度往往也与输入数据的规模有关。时间复杂度过高的低效算法可能导致我们在有生之年都等不到运行结果。

1.1例题2

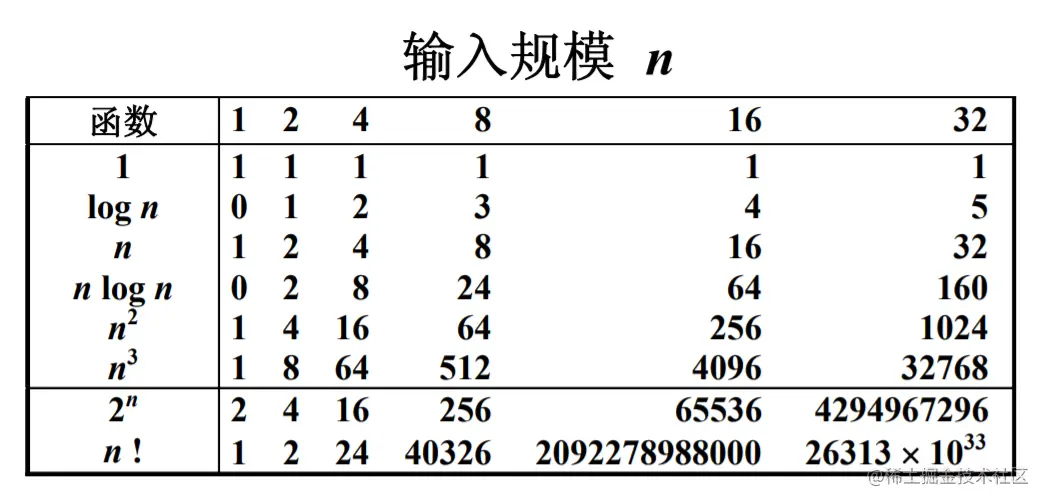
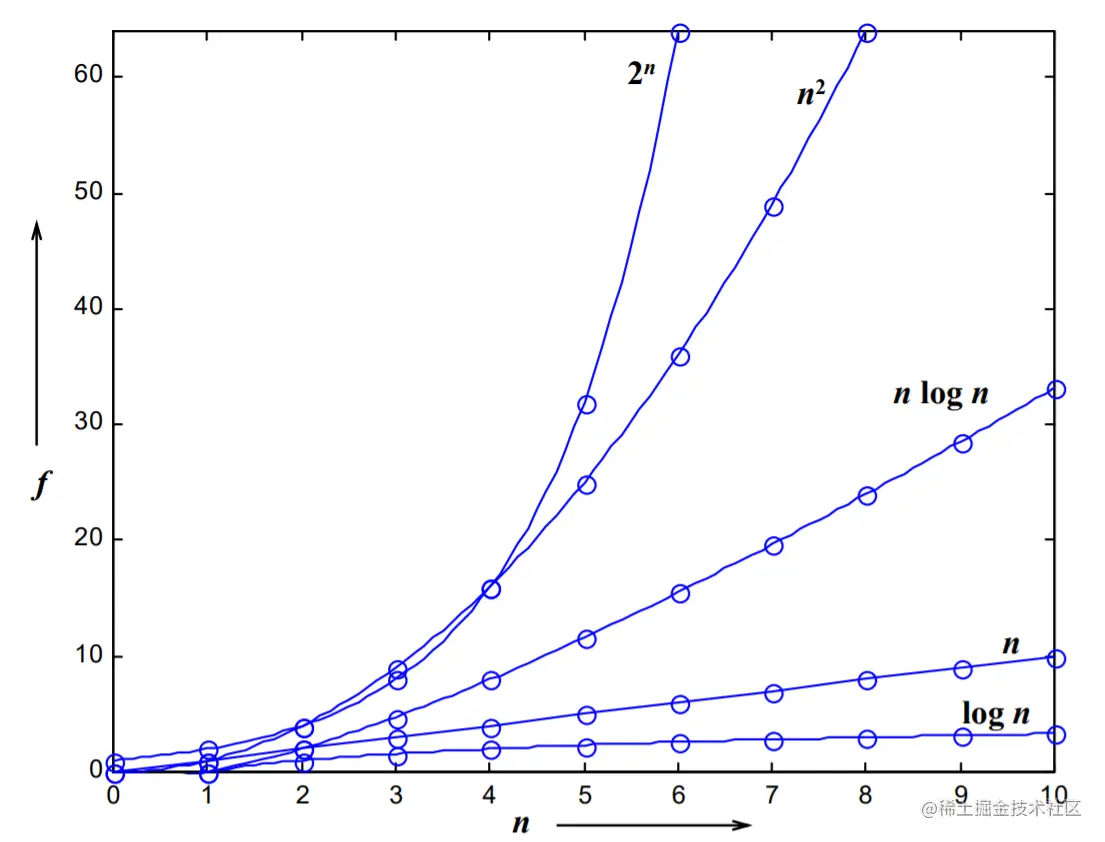
在分析一般算法的效率时，我们经常关注下面两种复杂度

1.3 最大子列和问题

int Max3( int A, int B, int C )
{ /* 返回3个整数中的最大值 */
    return A > B ? A > C ? A : C : B > C ? B : C;
}
 
int DivideAndConquer( int List[], int left, int right )
{ /* 分治法求List[left]到List[right]的最大子列和 */
    int MaxLeftSum, MaxRightSum; /* 存放左右子问题的解 */
    int MaxLeftBorderSum, MaxRightBorderSum; /*存放跨分界线的结果*/
 
    int LeftBorderSum, RightBorderSum;
    int center, i;
 
    if( left == right )  { /* 递归的终止条件，子列只有1个数字 */
        if( List[left] > 0 )  return List[left];
        else return 0;
    }
 
    /* 下面是"分"的过程 */
    center = ( left + right ) / 2; /* 找到中分点 */
    /* 递归求得两边子列的最大和 */
    MaxLeftSum = DivideAndConquer( List, left, center );
    MaxRightSum = DivideAndConquer( List, center+1, right );
 
    /* 下面求跨分界线的最大子列和 */
    MaxLeftBorderSum = 0; LeftBorderSum = 0;
    for( i=center; i>=left; i-- ) { /* 从中线向左扫描 */
        LeftBorderSum += List[i];
        if( LeftBorderSum > MaxLeftBorderSum )
            MaxLeftBorderSum = LeftBorderSum;
    } /* 左边扫描结束 */
 
    MaxRightBorderSum = 0; RightBorderSum = 0;
    for( i=center+1; i<=right; i++ ) { /* 从中线向右扫描 */
        RightBorderSum += List[i];
        if( RightBorderSum > MaxRightBorderSum )
            MaxRightBorderSum = RightBorderSum;
    } /* 右边扫描结束 */
 
    /* 下面返回"治"的结果 */
    return Max3( MaxLeftSum, MaxRightSum, MaxLeftBorderSum + MaxRightBorderSum );
}
 
int MaxSubseqSum3( int List[], int N )
{ /* 保持与前2种算法相同的函数接口 */
    return DivideAndConquer( List, 0, N-1 );
}

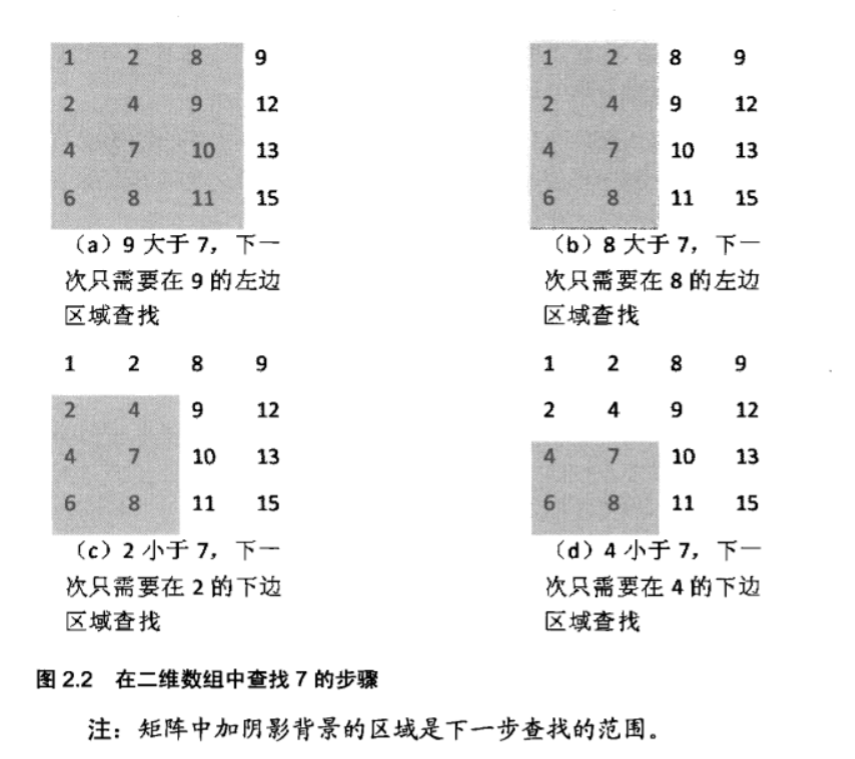
面试题3: 二维数组中的查找

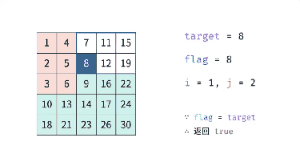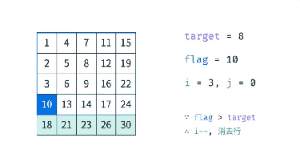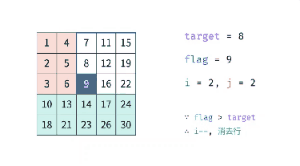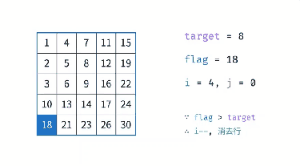
题目:在一个二维数组中，每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请完成一个函数，输入这样的个二维数组和一个整数，判断数组中是否含有该整数。

leetcode:leetcode-cn.com/problems/er…

GitHub:github.com/nateshao/le…

示例:
现有矩阵 matrix 如下：
[
  [1,   4,  7, 11, 15],
  [2,   5,  8, 12, 19],
  [3,   6,  9, 16, 22],
  [10, 13, 14, 17, 24],
  [18, 21, 23, 26, 30]
]
给定 target = 5，返回 true。

给定 target = 20，返回 false。

思路：

从右上角或者左下角开始匹配
注意：不能从左上角或者右下角开始

解法一：暴力破解，时间复杂度： $O(m * n)$ ，空间复杂度： $O(1)$

 /**
  * 解法一 ：暴力
  * 时间复杂度：O(nm)。二维数组中的每个元素都被遍历，因此时间复杂度为二维数组的大小。
  * 空间复杂度：O(1)。
  * 如果不考虑二维数组排好序的特点，则直接遍历整个二维数组的每一个元素，判断目标值是否在二维数组中存在。
  *
  * 依次遍历二维数组的每一行和每一列。如果找到一个元素等于目标值，则返回 true。
  * 如果遍历完毕仍未找到等于目标值的元素，则返回 false。
  * @param matrix
  * @param target
  * @return
  */
public boolean findNumberIn2DArray1(int[][] matrix, int target) {
     if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
         return false;
     }
     int rows = matrix.length, columns = matrix[0].length;
     for (int i = 0; i < rows; i++) {
         for (int j = 0; j < columns; j++) {
             if (matrix[i][j] == target) {
                 return true;
             }
         }
     }
     return false;
}

解法二：线性查找,时间复杂度 $O(M+N)$ ,空间复杂度 O(1)

/**
 * 解法二：线性查找
 * 时间复杂度 O(M+N) ：其中，N 和 M 分别为矩阵行数和列数，此算法最多循环 M+N次。
 * 空间复杂度 O(1)：x, y 指针使用常数大小额外空间。
 *
 * @param matrix
 * @param target
 * @return
 */
public boolean findNumberIn2DArray2(int[][] matrix, int target) {
        if (matrix.length == 0 || matrix[0].length == 0) {
            return false;
        }
        int x = 0;
        int y = matrix[0].length - 1;
        while (x < matrix.length && y >= 0) {
            int num = matrix[x][y];
            if (num == target) {
                return true;
            } else if (num > target) {
                y--;
            } else {
                x++;
            }
        }
        return false;
    
//        int i = matrix.length - 1, j = 0;
//        while (i >= 0 && j < matrix[0].length) {
//            if (matrix[i][j] > target) i--;
//            else if (matrix[i][j] < target) j++;
//            else return true;
//        }
//        return false;
}

参考链接：