1. 题目

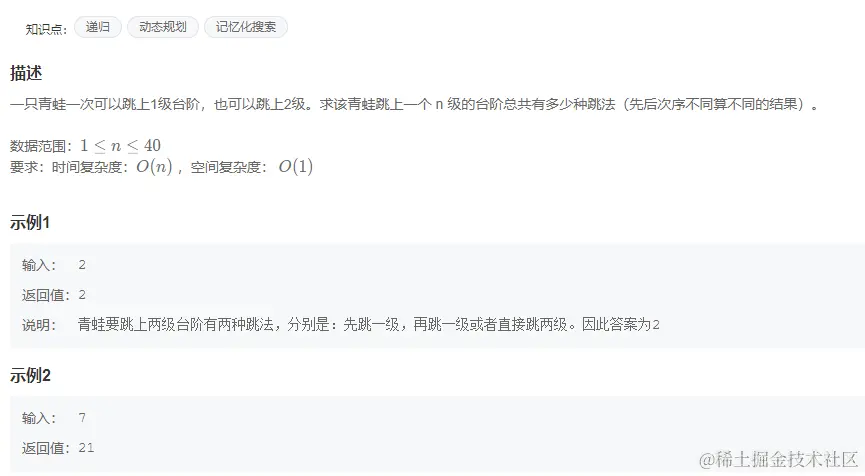
2. 题解

该题青蛙一次一跳；两次一跳我们可以罗列出前五跳的路线-可知：与斐波那契数列符合
我们可以得到 f(n) = f(n-1) + f(n-2)，采用递归耗时较长时间复杂度为 O(2^n) 空间复杂度为O(n)
此时需要考虑动态规划--

3. 动态规划

首先什么样的问题适合用动态规划解决？
符合 “一个模型三个特征” 的问题。
那么问题又来了，什么是“一个模型，三个特征”？
“一个模型”👉：指多阶段决策最优解模型；
“三个特征”👉：分别是最优子结构、无后效性和重复子问题。

核心代码

from ALG.warp import timer


@timer
def jump_floor(n):
    """
    耗时较长 时间复杂度为 O(2^n) 空间复杂度为O(n)
    """
    if n <= 1:
        return 1
    return jump_floor(n - 1) + jump_floor(n - 2)


@timer
def jump_floor2(number: int) -> int:
    """
    时间复杂度：O(n)，其中n为输入的数
    空间复杂度：O(1)，常数级变量，没有其他额外辅助空间
    """
    if number <= 1:
        return 1
    res = 0
    a = b = 1
    for i in range(2, number + 1):
        res = a + b
        a, b = b, res
    return res


@timer
def jump_floor3(n):
    if n <= 1:
        return 1
    res = 0
    a = b = 1
    ind = 2
    while ind < n + 1:
        res = a + b
        a = b
        b = res
        ind += 1
    return res


if __name__ == '__main__':
    print(jump_floor(8))
    print(jump_floor2(1000000))
    print(jump_floor3(1000000))

青蛙跳台阶

1. 题目

2. 题解

3. 动态规划

核心代码