本文已参与「新人创作礼」活动,一起开启掘金创作之路。
基本要求
开发上位机程序,要求有良好的界面,能提供关节空间下和笛卡尔坐 标下表示的目标位姿点和中间若干经过点的输入功能,进行轨迹规划, 并控制机械臂沿轨迹运动,最终完成目标抓取的任务。

基本概念
连杆长度 :2个相邻关节轴线之间的距离
连杆扭角 :2个相邻关节轴线之间的角度
连杆偏距 :2个关节坐标系的X轴之间的距离
关节角度 :关节变量 计算时需要加初始角度偏移
关节坐标系的建立
根据《机器人学导论》的内容,建立坐标系的规则如下:
-
坐标系Z轴确定规则:
如果关节是旋转的,Z轴按右手定则大拇指指向为正方向。
如果关节是滑动的,Z轴沿直线运动方向的正方向。
连杆长度D为关节变量。
-
X轴确定规则:
1)情况1:两关节Z轴既不平行也不相交
取两Z轴公垂线方向作为X轴方向。
2)情况2:两关节Z轴平行
此时,两Z轴之间有无数条公垂线,可挑选与前一关节的公垂线的一条公垂线
3)情况3:两关节Z轴相交
取两条Z轴的叉积方向作为X轴(叉积:向量积)
-
Y轴确定原则:右手定则
最终建立的机械臂坐标系如下图:
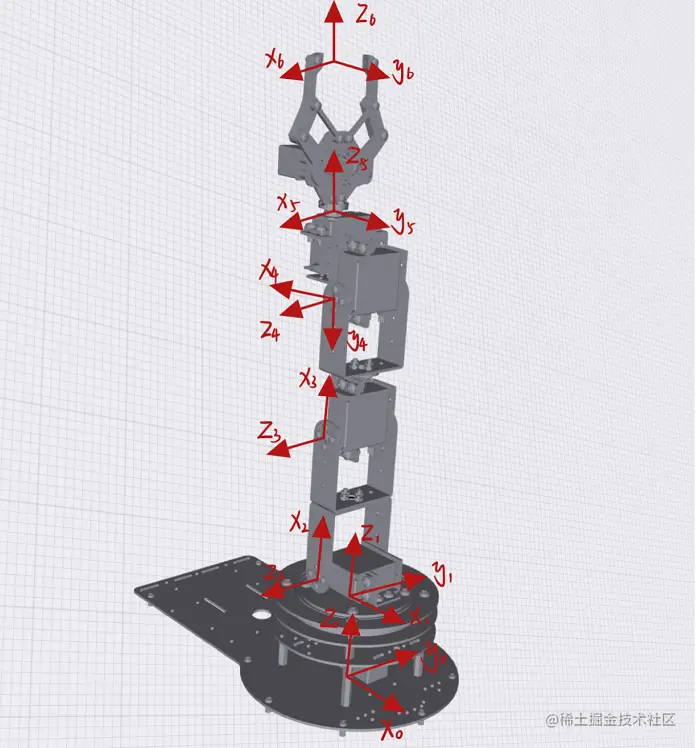
正运动学求解
DH参数表的建立
根据上述坐标系的建立,可以得到DH参数表如下:
| i | αi−1 | ai−1 | di | θi |
|---|
| 1 | 0 | 0 | 80 | θ1 |
| 2 | π/2 | 10 | 0 | θ2+π/2 |
| 3 | 0 | 105 | 0 | θ3 |
| 4 | 0 | 96 | -11 | θ4 |
| 5 | π/2 | 0 | 60 | θ5+π/2 |
| 6 | 0 | 0 | 95 | 0 |
根据书本中公式,ii−1T的一般表达式如公式(1)所示:
ii−1T=⎣⎡cθisθicαi−1sθisαi−10−sθisθicαi−1cθisαi−100−sαi−1cαi−10ai−1−sαi−1dicαi−1di1⎦⎤
可以计算得到工具坐标系相对于固定坐标系的位置和姿态,如下列所示
60T=10T⋅21T⋅32T⋅43T⋅54T⋅65T
逆运动学求解
将工具坐标系相对于固定坐标系的位姿齐次矩阵, 转化成笛卡尔坐标形式, 姿态 采用绕定轴 X-Y-Z 旋转 (RPY 角) 的形式描述, 其转化过程可描述如下:
BAT=[BAR0BAP00]
其中,
BAR=⎣⎡r11r21r31r12r22r32r13r23r33⎦⎤BAP=⎣⎡xyz⎦⎤
其转化为 RPY 角对应的公式为:
⎩⎨⎧θ=−asin(r31)ψ=atan2(r32/cos(θ),r33/cos(θ))ϕ=atan2(r21/cos(θ),r11/cos(θ))
对应的笛卡尔坐标为:
Carte =[x,y,z,θ,ψ,ϕ]
已知工具坐标系末端相对于固定坐标系的位置和姿态, 通过几何法对机械臂 的各关节角度进行求解。首先可以直接确定第一个关节和第五个关节的角度值, 第一 个关节的角度可以通过 x 和 y 直接确定, 第四个关节的角度值等于 ϕ, 即
θ1=atan2(y,x)θ5=ϕ
由于该机械辟只有五个自由度, 最后一个关节为空制夹爪的末端, 所以首先要对 工具坐标系末端相对于固定坐标系的位置进行处理, 分别减去夹爪在 x、y、z 方向上的分量,如下所示:
对于剩下的三个关节,求解其角度值可以看作是已知第三连杆的位姿求解平面三连杆中三个关节的角度值,其中,第三连杆末端的位置为x1,y1) ,倾斜角度为 ψ 。三连杆分别对应的角度为 θ1′,θ2′,θ3′,
对于三连杆所在的平面,有如下几何关系:
x1=l1⋅cosθ1′+l2⋅cos(θ1′+θ2′)+l3⋅cos(θ1′+θ2′+θ3′)y1=l1⋅sinθ1′+l2⋅sin(θ1′+θ2′)+l3⋅sin(θ1′+θ2′+θ3′) 令 m=l1⋅cosψ−x1,n=l2⋅sinψ−y1, 对于 θ1 有 θ1=(l1⋅cosθ1′+m)2+(l1⋅sinθ1′+n)2(θ1′+θ2′)=(l1⋅cos(θ1′+θ2′)+m)2+(l1⋅sin(θ1′+θ2′)+n)2 进而有, m⋅cosθ1′+n⋅sinθ1′=k1k1=2l1l22−l12−m2−n2m⋅cos(θ1′+θ2′)+n⋅sin(θ1′+θ2′)=k2k1=2l2l12−l22−m2−n2
令 b1=−2⋅n⋅k1,c1=k12−m2,Δ1=b12−4⋅a⋅c1, 当 Δ1<0 时, 则表示出现 非实数解的情况, 此时机械臂对于输入的笛卡尔坐标工作空间不可达。同理, 令 b2=−2⋅n⋅k2,c2=k22−m2,Δ2=b22−4⋅a⋅c2, 当 Δ2<0 时, 则表示工作空间不可 达。
根据书本公式[1],可以解得
θ1′=atan2(n,m)±atan2(a−k12),k1)θ1′+θ2,=atan2(n,m)±atan2(a−k22),k2)
最终,根据θ1′+θ2′+θ3=ψ可以求解出平面三连杆中各个关节的倾斜角度。
多解下解的选取
平面三连杆在求解时会出现多解的情况,经过思考分析,对多解情况提出了一种可行的方案,如下图所示
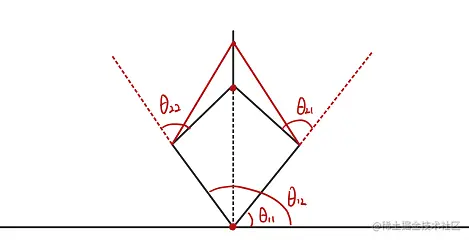
上式的θ1′有两组解,由于机械臂的臂长l1和 l2的长度不同,所以会有:
θ11+θ12>θ21+θ22
此处 θ22<0, 并且 θ21>θ11, 由此关系可以对两组解进行区分。
则可以求出机械臂第 2、3、4 关节的角度
θ2=θ1′−90θ3=θ2′θ4=θ3′
最终可得机械臂逆运动学的解
JVar =[θ1,θ2,θ3,θ4,θ5]
源码下载
方式一:
多功能视觉引导5-DOF机械臂实现
方式二:
关注公众号技术开发小圈,在菜单栏中点击项目分享,即可获得百度网盘链接。