致初学者的深度学习入门系列（一）—— 简单神经网络基础

Rosen_
254 阅读8分钟

本文已参与「新人创作礼」活动，一起开启掘金创作之路。

简单神经网络基础

1. 基本符号与运算

x：输入向量

w：权重

b：偏置

g（）：激活函数

a：输出向量

y：输出结果

xw[i]⟶z[i]=w[i]x+b[i]⟶a[i]=g(z[i])b[i]\begin{aligned} & x\\ & w^{[i]}\longrightarrow z^{[i]}=w^{[i]}x+b^{[i]}\longrightarrow a^{[i]}=g(z^{[i]})\\ & b^{[i]} \end{aligned}

经过激活函数后得到输出向量

A[i]=[a11a12⋯⋯a1m⋅⋅⋅⋅⋅⋅⋅⋅⋅an1an1⋯⋯anm]A^{[i]}= \begin{bmatrix} a_{11}&a_{12}&\cdots&\cdots&a_{1m}\\ ·&·&&&· \\ ·&&·&&·\\ ·& & &·&·\\ a_{n1}&a_{n1}&\cdots&\cdots&a_{nm} \end{bmatrix}

横向代表different example(维度)，纵向代表different indices(特征)

2. 激活函数

常见激活函数：

sigmoid函数

g(x)=11+e−xg(x)=\dfrac{1}{1+e^{-x}}

​ 容易受到梯度饱和现象，在绝对值较大的时候对于微小改变不敏感，适用于二元分类输出层。

tanh函数

g(x)=ex−e−xex+e−xg(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}

​ 数据中心为零点，可以去中心化，但同样会有梯度饱和现象。

ReLU函数

g(x)=max(0,x)g(x)=max(0, x)

​ 目前使用最为广泛，效果好且速度快，但对于负数领域直接忽略。

Leaky ReLU函数

g(x)=max(0.01x,x)g(x)=max(0.01x, x)

**思考：**我们可以发现上述激活函数全都是非线性的，那么激活函数是否一定要为非线性的呢？

​ 假设

g(x)=xg(x)=x

​ 那么有

a[1]=w[1]x+b[1]a[2]=w[2]a[1]+b[2]=w[2]w[1]x+w[2]b[1]+b[2]=w′x+b′a^{[1]}=w^{[1]}x+b^{[1]}\\ a^{[2]}=w^{[2]}a^{[1]}+b^{[2]}=w^{[2]}w^{[1]}x+w^{[2]}b^{[1]}+b^{[2]}=w'x+b'

​ 网络层之间可以线性叠加，所以无论最终网络有多少层，都可以等效成一层。所以网络无论多复杂都只能解决线性回归问题。

3.随机权重初始化

​ 如果初始化权重均为0，每个隐含层单元的计算结果均相等，同样无论网络有多复杂，节点再多计算结果都相同。但是如果初始化权重的数值很大，当激活函数为sigmoid或者tanh函数时，恰好落在斜率很小的平缓区，学习率也会很慢。所以一般初始化权重的数值都为接近0的随即小数。

4. 运算过程

对于输入层，我们默认

X=A[0]X=A^{[0]}

所以，前向传播的过程：

Z[l]=W[l]A[l]+b[l]A[l]=g[l](Z[l])Z^{[l]}=W^{[l]}A^{[l]}+b^{[l]}\\ A^{[l]}=g^{[l]}(Z^{[l]})

上一层的输出值即为本层的输入值。

对于输出层，有

Y^=g[L](Z[L])=A[L]\hat{Y}=g^{[L]}(Z^{[L]})=A^{[L]}

​ 我们可以理解为，网络结构从前到后依次从低层次特征到高层次特征进行分类，最终在输出层对总类别进行分类。如下列对一张人脸进行分类，我们首先是对一些边缘梯度等基本特征进行分类，再到眼睛、嘴巴等部位，最终对不同人脸进行分类。

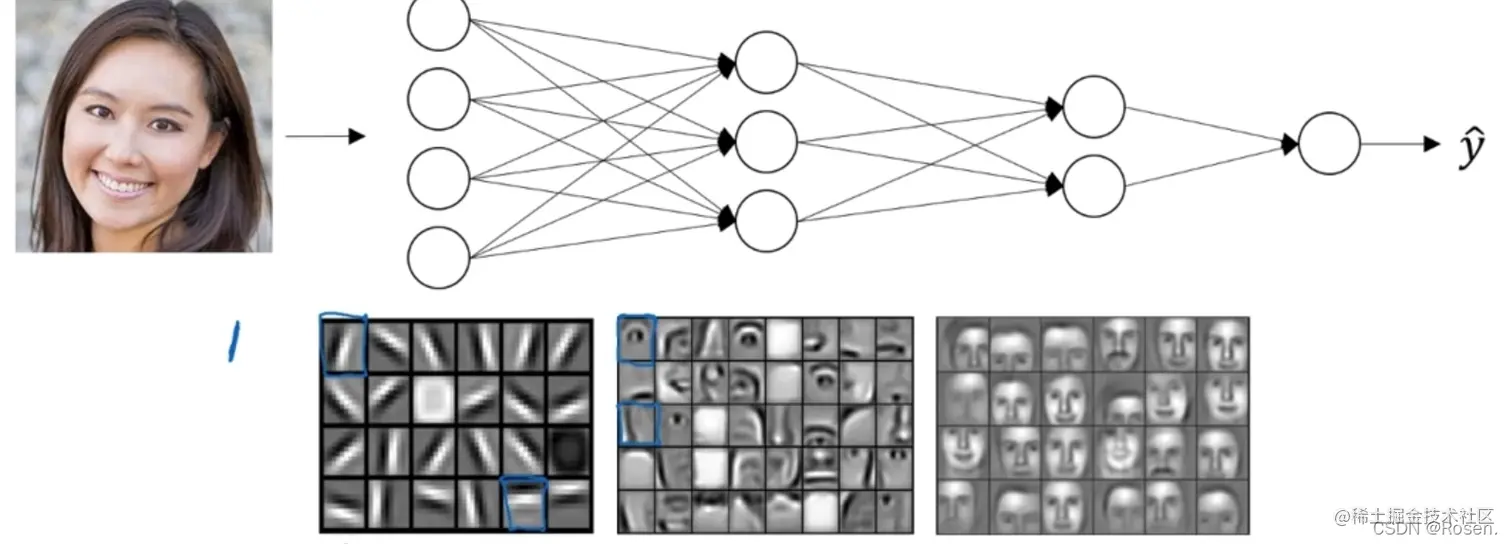
​ 因此我们可以把现实中需要解决的实际问题看成是一个数学问题，所谓的识别分类不过是找出对象的分布，并在学习过程中进行拟合，求解出一个复杂的多元多次曲面（理论上只要两个类别在特征之间存在差异就可以用多元曲面进行分割）。神经网络就是求解这个曲面的一个工具，其中的权重和偏置就决定了曲面的特性。

5. 前向传播和反向传播

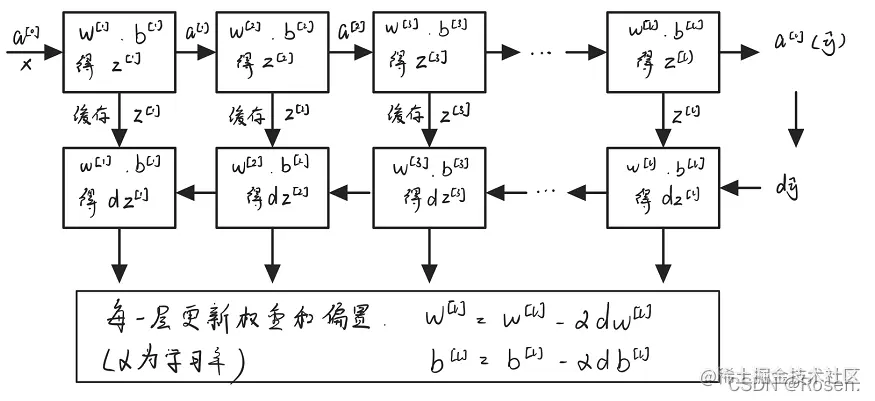
在这里插入图片描述

​ 首先前向传播从隐含层一直到输出层，计算出输出层结果后，对z分别求关于w和b的导数，更新当前层的w和b后反向传播至上一层计算更新参数。

6. 参数和超参数

神经网络中的参数和超参数

**参数：**权重w，偏置b；

**超参数：**学习率a，隐含层、输出层节点数n、L，……

超参数特点：其设置直接决定了最终计算得到的参数。

7. 方差和偏差

训练集误差（Train Set Error）1%15%15%0.5%
验证集误差（Dev Set Error）11%16%30%1%
高方差高偏差高方差&高偏差低方差&低偏差

以上均是相对于基本误差而定的。

方差：评判预测效果的标准

偏差：评判训练结果的标准

基本误差：取决于数据集的质量

如何诊断要得到一个好的模型？

偏差高？-->尝试优化网络和训练算法

方差高？-->采用更多数据以及正则化等操作

8. 正则化

​ 正则化是机器学习中常用的一种方法，主要用于控制模型的复杂度，减小过拟合。最基本的正则化方法是在原目标（代价）函数 中添加惩罚项，对复杂度高的模型进行“惩罚”。

​ 数学表达式

J^(w;,X,y)=J(w;,X,y)+αΩ(w)Ω()为惩罚项，α控制正则化的强弱\hat{J}(w;, X, y)=J(w;, X, y)+\alpha \Omega(w)\\ \Omega()为惩罚项，\alpha控制正则化的强弱

​ 其中X, y为训练样本和标签，w为权重系数向量，J()为目标函数

以下以准则函数为以下形式为例：

J=1m∑i=1nL(y^[i],y[i])J=\dfrac{1}{m}\sum_{i=1}^{n}L({\hat{y}^{[i]}}, y^{[i]})
  • L1正则化

准则函数

J(w[1],b[1],⋯ ,w[l],b[l])=1m∑i=1nL(y^[i],y[i])+λ2m∑l=1L∥w[l]∥J(w^{[1]}, b^{[1]}, \cdots, w^{[l]}, b^{[l]})=\dfrac{1}{m}\sum_{i=1}^{n}L({\hat{y}^{[i]}}, y^{[i]})+\dfrac{\lambda}{2m}\sum_{l=1}^{L}\parallel w^{[l]}\parallel

假设W为二维的，则有

L=∣w1∣+∣w2∣L=|w^1|+|w^2|

在二维坐标系中对应为一个方框。

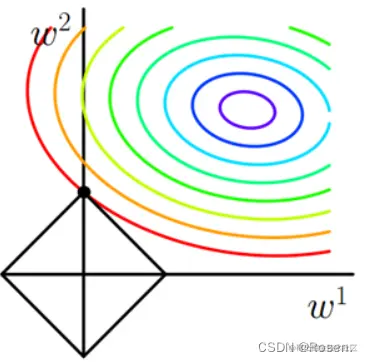
在这里插入图片描述

​ 很多时候最优解就落在方形的角点处，此时就会有一个权重为0。而对应到高维度的情况，将会有更多的权重值为0。在神经网络中权重为0代表该节点被删除，这也就是L1正则化可以产生稀疏模型的原因。

  • L2正则化

准则函数

J(w[1],b[1],⋯ ,w[l],b[l])=1m∑i=1nL(y^[i],y[i])+λ2m∑l=1L∥w[l]∥2J(w^{[1]}, b^{[1]}, \cdots, w^{[l]}, b^{[l]})=\dfrac{1}{m}\sum_{i=1}^{n}L({\hat{y}^{[i]}}, y^{[i]})+\dfrac{\lambda}{2m}\sum_{l=1}^{L}\parallel w^{[l]}\parallel^2

同样我们假设W为二维的，则有

L=∥w1∥22+∥w2∥22L=\parallel w_1\parallel_2^2+\parallel w_2\parallel_2^2

在二维坐标系中对应为一个圆，

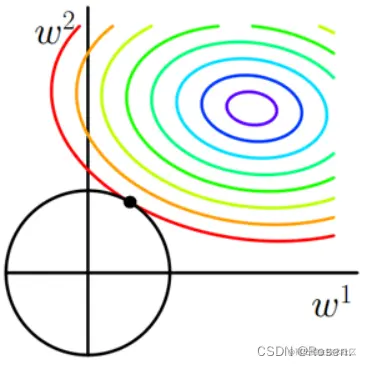
在这里插入图片描述

​ L2正则化在拟合过程中通常都倾向于让权值尽可能小，最后构造一个所有参数都比较小的模型。因为一般认为参数值小的模型比较简单，能适应不同的数据集，也在一定程度上避免了过拟合现象。

其中

惩罚项我们也可以采用弗罗贝尼乌斯范函数∥w[l]∥F2=∑i=1n[l−1]∑j=1n[l](wij[l])2惩罚项我们也可以采用\quad\text{弗罗贝尼乌斯范函数} \parallel w^{[l]}\parallel^2_F=\sum_{i=1}^{n^{[l-1]}}\sum_{j=1}^{n^{[l]}}(w^{[l]}_{ij})^2

权重更新采用权重衰减策略：

dw[l]=反向传播后的结果+λmw[l]dw^{[l]}=\text{反向传播后的结果}+\dfrac{\lambda}{m}w^{[l]}

m为一个mini-batch的大小

权重衰减

w[l]=w[l]−αdw[l]=w[l]−αλmw[l]−反向传播结果=（1−αλm）w[l]−反向传播结果w^{[l]}=w^{[l]}-\alpha dw^{[l]}=w^{[l]}-\alpha \dfrac{\lambda}{m}w^{[l]}-\text{反向传播结果}=（1-\alpha \dfrac{\lambda}{m}）w^{[l]}-\text{反向传播结果}

相当于原来的权重进行了缩小

**思考：**正则化使得权重衰减，为什么可以防止过拟合？

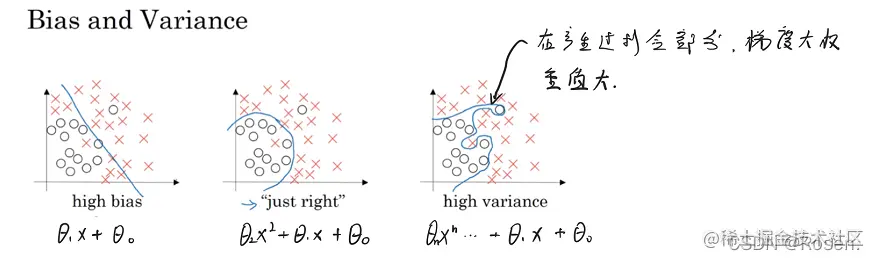
在这里插入图片描述

​ 当上市中的权重衰减逐渐接近于0时，相当于网络的节点逐渐减少，网络变得简单。这时候网络将由过拟合状态（最右图）逐渐向左边两个状态过渡，以此防止过拟合。

  • Dropout正则化

​ 以某个随机概率将网络中的节点权重设置为0（相当于删除该节点），使得网络逐渐变得简单，也可以起到防止过拟合的效果。

9. 归一化输入特征

​ 将不同输入特征归一化到[0,1]，方差为1的区间内，防止结果受到数值较大特征的过多影响。

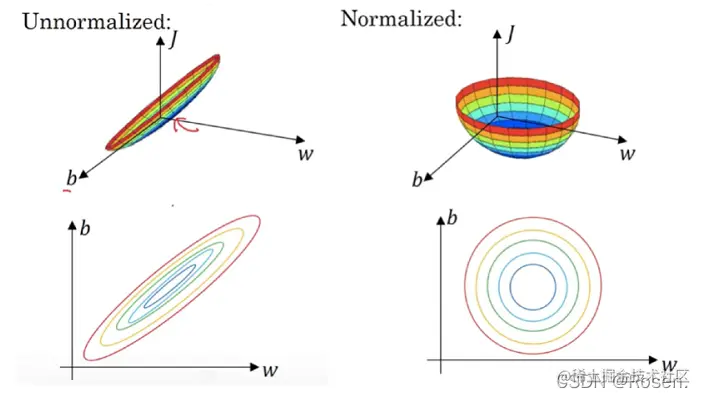
在这里插入图片描述

归一化后不仅可以减小特征之间的数值影响，还可以加快收敛速度。

10. 梯度检验

dθ˙=J(θ1,θ2,⋯ ,θi+ε,⋯ )−J(θ1,θ2,⋯ ,θi−ε,⋯ )2ε≈dθ[i]=∂J∂θi\begin{aligned} d\dot{\theta}&=\dfrac{J(\theta_1, \theta_2, \cdots, \theta_i+\varepsilon, \cdots)-J(\theta_1, \theta_2, \cdots, \theta_i-\varepsilon, \cdots)}{2\varepsilon}\\ & \approx d\theta^{[i]}=\dfrac{∂J}{∂\theta_i} \end{aligned}

检验

∥dθ˙−dθ∥2<10−7\parallel d\dot\theta -d\theta \parallel_2 < 10^{-7}

若检验出有误，需检验每一项是否出现问题。

**注：**梯度检验和Dropout正则化一般不共用。

11. 优化算法

  • mini-batch梯度下降法（BGD）

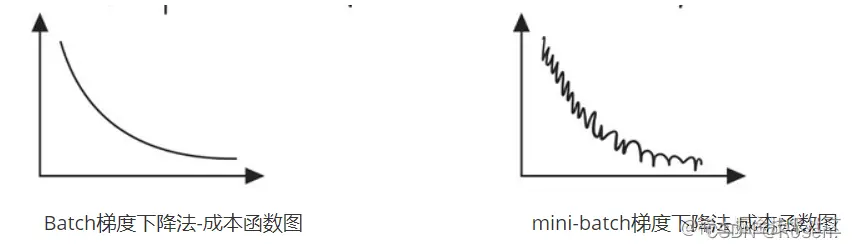
在这里插入图片描述

  1. 当mini-batch大小等于batch size单词迭代耗时过长；
  2. 当mini-batch大小等于1，称为随机梯度下降法（SGD）——效率低下。
  3. 当mini-batch大小取合适时

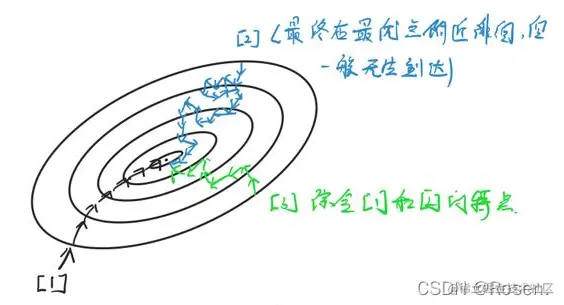
在这里插入图片描述

优点：可以减少单次迭代的耗时，mini-batch可以加快参数的更新速度，提高训练速度。

  • 指数加权平均

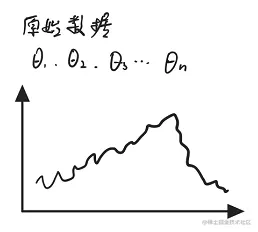
<img src="C:\Users\10184\AppData\Roaming\Typora\typora-user-images\image-20210901150620161.png" alt="image-20210901150620161" style="zoom:80%;" />

<img src="C:\Users\10184\AppData\Roaming\Typora\typora-user-images\image-20210901150710138.png" alt="image-20210901150710138" style="zoom:80%;" />

v0=0vt=βt−1+(1−β)θtv_0=0\\ v_t=\beta_{t-1}+(1-\beta)\theta_t

β\beta越大，加权平均的范围越大，曲线就越平滑。

示例：

v100=0.1θ100+0.1×0.9θ99+0.1×0.92θ98+0.1×0.93θ97+⋯当β=0.9时,0.1×(0.9)10≈0.35当β=0.98时,0.1×(0.9)50≈0.35(加权平均范围更大)v_{100}=0.1\theta_{100}+0.1\times0.9\theta_{99}+0.1\times0.9^{2}\theta_{98}+0.1\times0.9^{3}\theta_{97}+\cdots\\ \text{当}\beta=0.9\text{时},0.1\times(0.9)^{10}\approx 0.35\\ \text{当}\beta=0.98\text{时},0.1\times(0.9)^{50}\approx 0.35\text{(加权平均范围更大)}\\

偏差修正

以上加权平均在初始时偏差较大，需进行修正：

vt1−βt\dfrac{v_t}{1-\beta^t}

​ 随着t逐渐增大，修正效果逐渐减弱。

  • Momentum梯度下降法

    在迭代的过程中，对于纵轴我们希望学习率较小，以至于摆动不会太大。对于横轴我们希望学习率较大，以此来提高学习速度。

    因此我们在更新权值时，有

    vdw=βvdw+(1−β)dwvdb=βvdb+(1−β)dbv_{dw}=\beta v_{dw}+(1-\beta)dw\\ v_{db}=\beta v_{db}+(1-\beta)db

    如下图所示，Momentum梯度下降法可以加快梯度下降的速度。

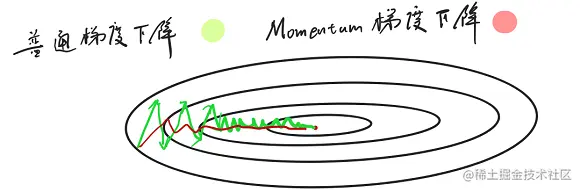
在这里插入图片描述

  • RMSprop优化算法

    原理与Momentum算法原理大致相同，形式为：

    Sdw=βSdw+(1−β)dw2w=w−αdwSdw+ε(较小)Sdb=βSdb+(1−β)db2b=b−αdbSdb+ε(较大)S_{dw}=\beta S_{dw}+(1-\beta)dw^2 \quad w=w-\alpha \dfrac{dw}{\sqrt{S_{dw}}+\varepsilon}\text{(较小)}\\ S_{db}=\beta S_{db}+(1-\beta)db^2 \quad b=b-\alpha \dfrac{db}{\sqrt{S_{db}}+\varepsilon}\text{(较大)}

    纵轴上的变化很多时候是由偏置b引起的，所以抑制b可以减小纵轴上的摆动。

  • Adam优化算法（Momentum和RMSprop的结合）

步骤：

​ 初始化：

vdw=0,Sdw=0.vdb=0,Sdb=0.v_{dw}=0, S_{dw}=0. \quad v_{db}=0,S_{db}=0.

​ 迭代：

vdw=β1vdw+(1−β1)dwvdb=β1vdb+(1−β1)dbSdw=β2Sdw+(1−β2)dwSdb=β2Sdb+(1−β2)dbv˙dw=vdw(1−β1t)v˙db=vdb(1−β1t)S˙dw=Sdw(1−β2t)S˙db=Sdb(1−β2t)w=w−αv˙dwS˙dw+εb=b−αv˙dbS˙db+εv_{dw}=\beta_1v_{dw}+(1-\beta_1)dw \quad v_{db}=\beta_1v_{db}+(1-\beta_1)db\\ S_{dw}=\beta_2S_{dw}+(1-\beta_2)dw \quad S_{db}=\beta_2S_{db}+(1-\beta_2)db\\ \dot{v}_{dw}=\dfrac{v_{dw}}{(1-\beta^t_1)} \quad \dot{v}_{db}=\dfrac{v_{db}}{(1-\beta^t_1)}\\ \dot{S}_{dw}=\dfrac{S_{dw}}{(1-\beta^t_2)} \quad \dot{S}_{db}=\dfrac{S_{db}}{(1-\beta^t_2)}\\ w=w-\alpha\frac{\dot{v}_{dw}}{\sqrt{\dot{S}_{dw}}+\varepsilon}\quad b=b-\alpha\frac{\dot{v}_{db}}{\sqrt{\dot{S}_{db}}+\varepsilon}

12. 学习率衰减

​ 在训练过程中学习率逐渐衰减，学习初期较大的学习率可加快迈进的步伐，当逐渐开始收敛时，小的学习率可以使其不会一下跃过最优点，造成发散。

学习率衰减的几种形式：

1.α=11+decay_rate∗epoch_num⋅α02.α=0.95epoch_num⋅α03.α=kepoch_num⋅α0\begin{aligned} & 1. \alpha =\dfrac{1}{1+decay\_rate*epoch\_num}·\alpha_0\\ & 2. \alpha = 0.95^{epoch\_num}·\alpha_0\\ & 3. \alpha =\dfrac{k}{\sqrt{epoch\_num}}·\alpha_0\\ \end{aligned}

13. Batch Normalization（BN）算法

有前面的归一化输入特征我们知道，归一化操作通过处理当前层的输入特征有利于对当前层的训练，那么如果我们想要实现更优的效果，可否对每一层都进行归一化呢，于是批量归一化横空出世。

实现：

对每一层有

μ=1m∑i=1nz[i]σ2=1m∑i=1n(zi−μ)2znorm[i]=z[i]−μσ2+ε将每一层的z值进行归一化处理也可以用z^norm[i]=λznorm[i]+β来实现\mu = \dfrac{1}{m}\sum_{i=1}^{n}z^{[i]}\quad \sigma^2=\dfrac{1}{m}\sum_{i=1}^{n}(z_i-\mu)^2\\ z_{norm}^{[i]}=\dfrac{z^{[i]}-\mu}{\sqrt{\sigma^2+\varepsilon}}\quad\text{将每一层的z值进行归一化处理}\\ \text{也可以用}\quad \hat{z}_{norm}^{[i]}=\lambda z_{norm}^{[i]}+\beta \quad\text{来实现}

BN算法通常和mini-batch算法一起使用，其可以减少其他层参数对于当前层的影响，提高每一层的独立性。

14. Softmax激活函数

ajL=ezjL∑kezkLa_j^L=\dfrac{e^{z_jL}}{\sum_{k}e^{z_kL}}

​ 常运用于多分类网络的输出层。将输出层的结果向量进行归一化后输出。

15. 单一数字评估指标

TP：预测结果中于实际相符的个数（实际为正，预测为正）

FP：预测结果中于实际不相符的个数（实际为负，预测为正）

FN：实际存在但预测结果中不存在的项个数（实际为正，预测为负）

查准率P（Precision）：当实际为正时，预测也为正的概率。

查全率R（Recall）：当预测为正时，实际也为正的概率。

P=TPTP+FPR=TPTP+FNP=\dfrac{TP}{TP+FP}\quad \quad R=\dfrac{TP}{TP+FN}

由于两个指标我们很难同时进行衡量，所以将P和R结合，可以得到F1 Score：

F1=21P+1RF1=\dfrac{2}{\dfrac{1}{P}+\dfrac{1}{R}}
avatar
文章
阅读
粉丝