关于移位运算
已知 g(x)=z 和 g′(f(x))=z′
若 f(z)=z′, 则说明 g 与 g′ 同构
右移
定义 原码的右移运算 g(x)=x>>1 为真值除以 2 并向下取整
其在补码域上的同构变换 g′([x]补)=[x]补>>1
其中 f(x)=[x]补
正数
令 x=+0100(4), 则 x>>1=+0010(2)
已知 [x]补=0,0100, 则 [x]补>>1=?,0010
为了使 g 和 g′ 同构, 则 [x>>1]补=[x]补>>1, 即 ?=0
① 正数原码的右移符号位不需要动, 符号位的下一位补 0
② 正数补码可以说符号位不动, 补充位补 0, 也可以说符号位跟着一起移动, 补充位与符号位相同
负数
令 x=−0100(−4), 则 x>>1=−0010, [x>>1]补=11110
[x]补=1,1100, [x]补>>1=?1110, 为了同构, ?=1
① 负数的原码右移规则与正数的一致
② 负数的补码右移符号位需要移动, 补充位与符号位相同, 另一种等价的说法是, 符号位不动, 补充位补 1
补充
原码右移符号位如果一起动的话, 正数还行, 00100>>1 变成了 ?0010, 令 ?=0 结果无影响, 负数的话, −0100(−4)>>1 变成了 ?1010(±10), 无论符号位是什么都不正确
左移
定义左移是真值乘以 2
正数
令 x=+1000(8), x<<1=+0000(0)(这里溢出了)
其补码为 [x]补=0,1000, 左移为 [x]补<<1=?,000?
为使 [x<<1]补=0,0000=[x]补<<1, 故两个 ?=0
负数
令 −0001(−1), x<<1=−0010(−2), 因此 [x<<1]补=1,1110, 其补码为 [x]补=1,1111, 左移 [x]补<<1=1,110?, 得到 ?=0
因此原码和补码的左移都是补 0, 符号位不动
乘法
原码一位乘
使用变形补码(符号位是2位)的原因是为了实现乘时溢出无影响, 因为乘时需要右移, 比如 00,11 + 00,11 = 01,10, 为了右移不改变符号位, 所以需要再多一位符号位, 这样即使溢出了也会在右移时消除溢出的影响, 如果用一位符号位, 则会出现 0,11 + 0,11 = 1,10, 右移时就变成了 1,11, 变成了一个负数
令 x=x0x1x2⋯xn 以及 y=y0y1y2⋯yn
其中 x0 和 y0 是符号位
已知 y=y1×2−1+y2×2−2+⋯+yn×2−n
则 x×y=x×(y1×2−1+y2×2−2+⋯+yn×2−n)
根据秦九韶算法可得
x×y=2−1(xy0+2−1(xy2+2−1⋯(xyn+0)))
即原码的一位乘法是最低位 yn 乘上 x, 再 右移 一位(2−1), 加上次低位 yn−1 乘以 x, 右移, 反复如此...
由于 y 只有 0 和 1 两种状态, 因此 yi×x 等价于加或者不加 x
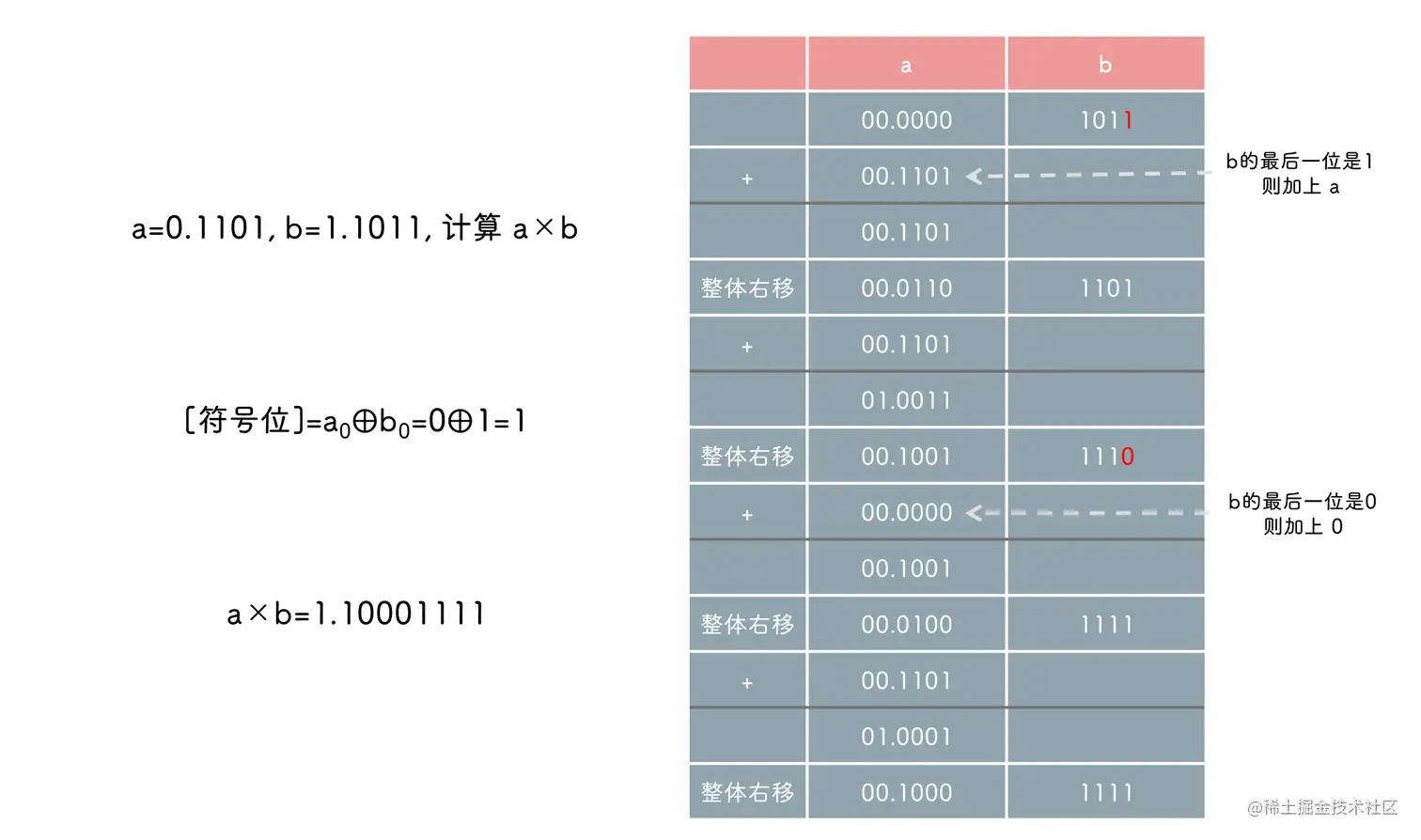
原码两位乘
两位乘存在 4 种情况
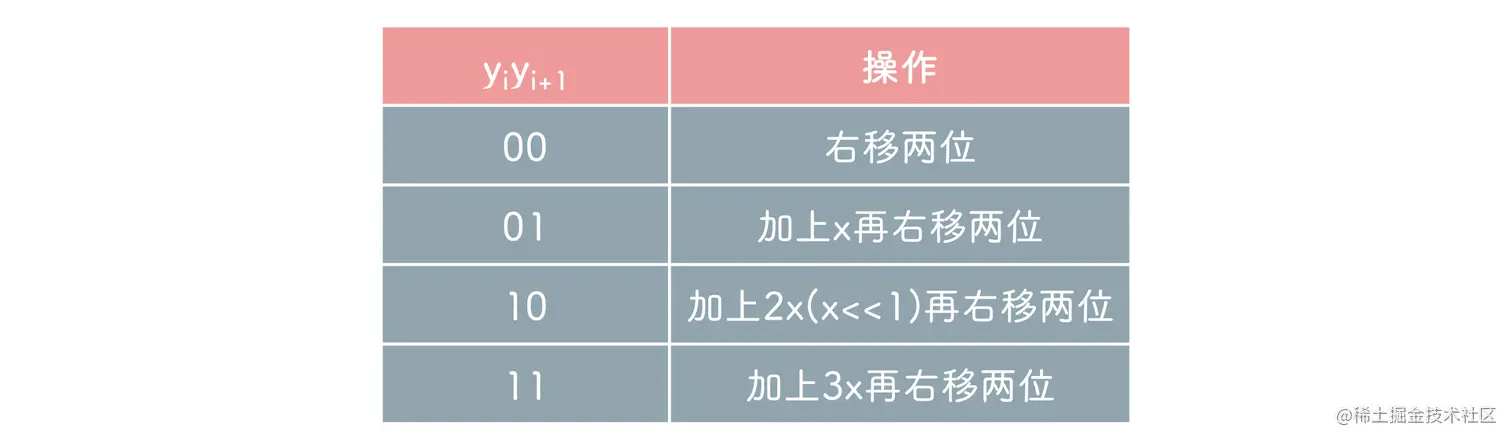
3x 比较特殊, 不能通过直接右移得到, 因此这里采用先 -x 再 +4x 的策略
这里 4x 刚好能够被更高位的两位乘代替, 相当于 进1 , 把处理交给下一次乘法, 因此实际情况为
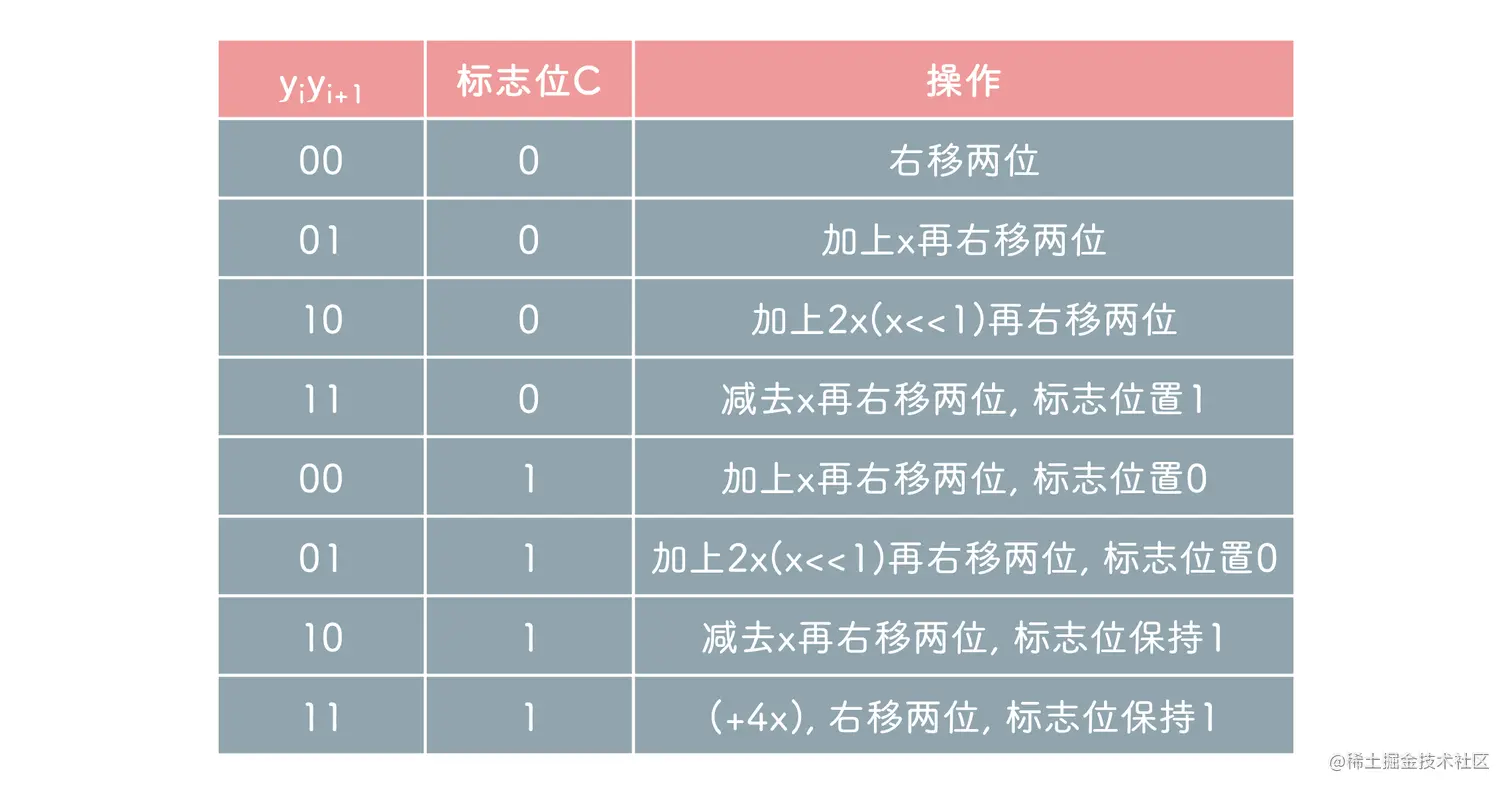
同一位乘相同, 两位乘也需要使用变形补码, 不过这里符号位是 3 位, 因为有加 2x 的存在, 如 000.11... + 001.10...(2x) = 010.01 , 为了保持真实的符号位, 需要 3 位符号位
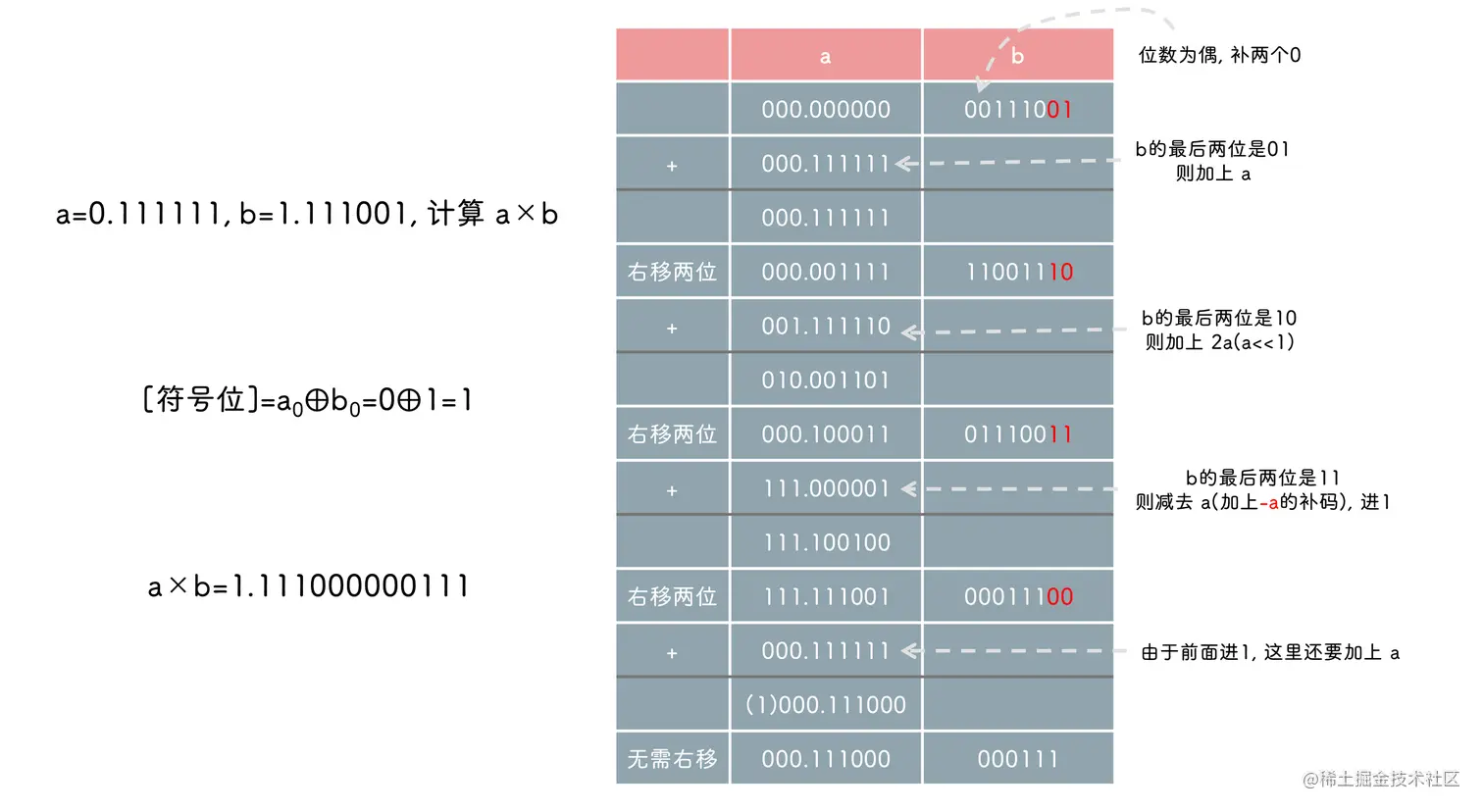
这里为了防止不够两位乘, 因此若 b 的位数为奇数, 则补一个 0, 为偶数, 则补两个 0
补充 0 是为了与进位的 1 相结合, 位数为偶数时可能最高两位还会进 1 , 因此必须补两个 0 , 为奇数时, 进 1 最多到 10, 不会再进了, 因此补 1 个就够了
由于补充位的存在, b 的所有位都已经移除, 因此最后不需要再右移两位, 但是奇数位的乘数只补充了一个 0, 因此最后还要右移一位把 b 的所有位移除

补码一位乘
乘数为正数时
[x×y]补=[x]补×[y]补=[x]补×y
即按照原码一位乘的规则, 只不过乘的不是 x, 而是 [x]补, 并且由于 y 是正数, 正数的补码等于原码...
x是正是负无所谓, 因为乘法实际上是一个个加法, 补码求和还是补码, 因此并不需要关心 x
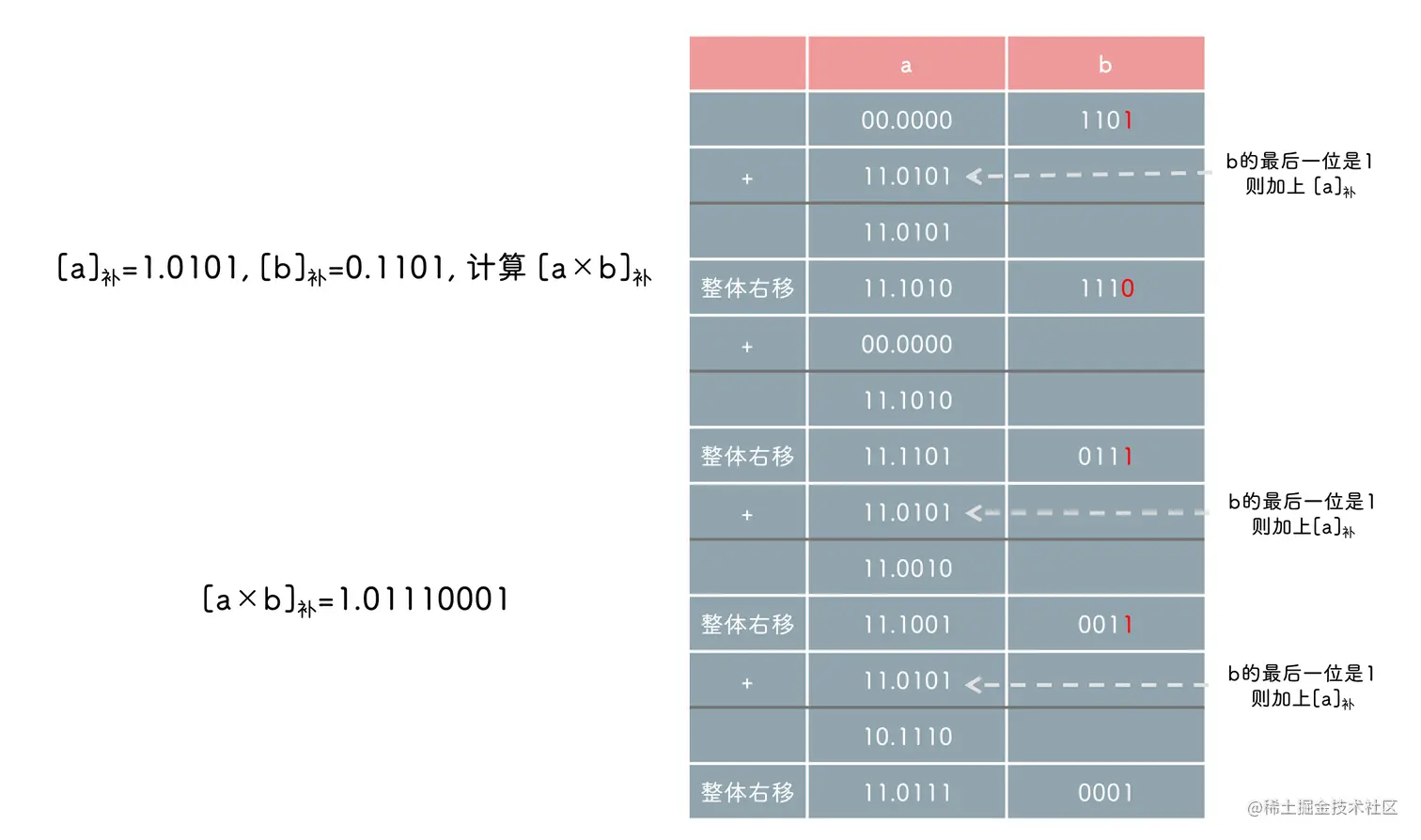
这里有个好处是, 符号位可以参与运算, 所得结果即最终结果
乘数为负数时
已知 [y]补=2+y (mod 2) (y≤0)
例如 y=−0.0101, 则 [y]补=2−0.0101=1.1011
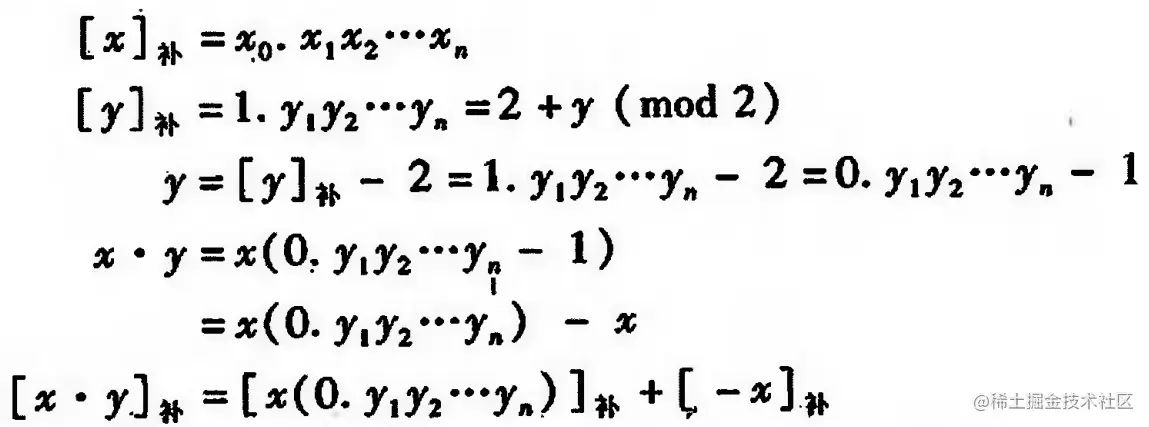
也就是说可以先不考虑 [y]补 的符号, 算完后再加上 [−x]补
已知 [x]补 求 [−x]补 只需要将各位取反(包括符号位)再末尾加 1
① [x]补=0.1101, 则 [−x]原=1.1101, [−x]补=1.0011
② [x]补=1.1101, 则 [−x]原=0.0011, [−x]补=0.0011
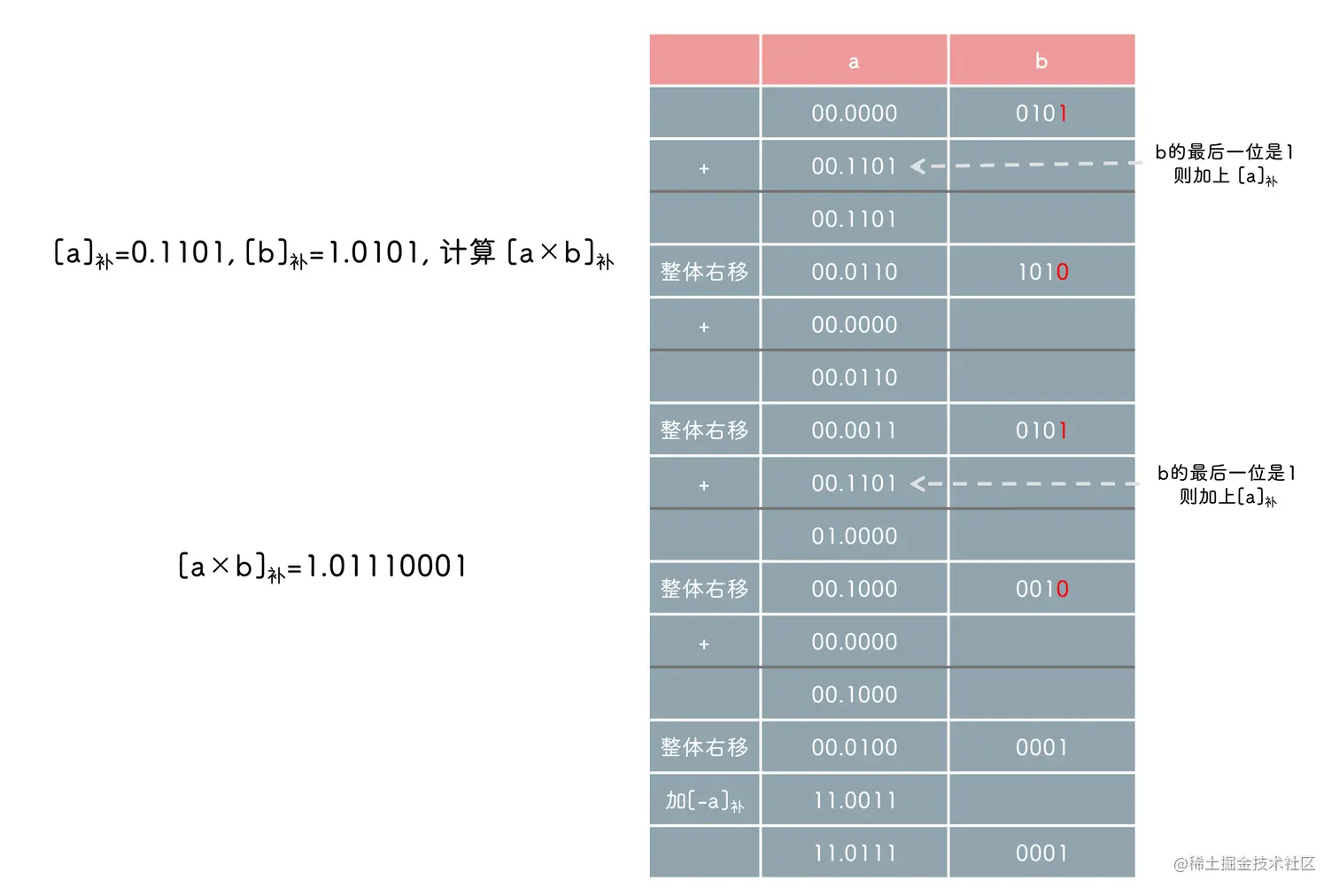
Booth 算法
补码一位乘的通用公式:
[x×y]补=[x]补(0.y1y2⋯yn)−[x]补×y0
当 y 为正数时, y0=0, 因此不需要 [−x]补 修正, 当 y 为负数时, 需要 [−x]补 修正
注意 [−x]补=−[x]补 mod 2
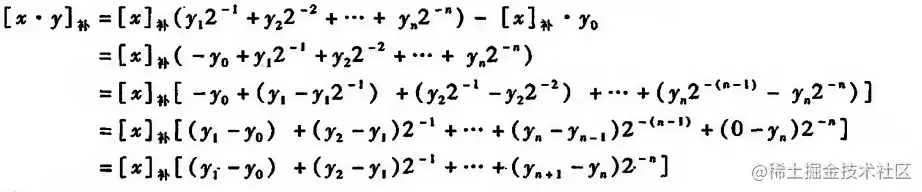
上图涉及一个附加位 yn+1=0, 上图与原码一位乘时展开很相似, 只不过用 yn+1−yn 代替 yn
因此 booth 算法的核心与 yiyi+1 有关
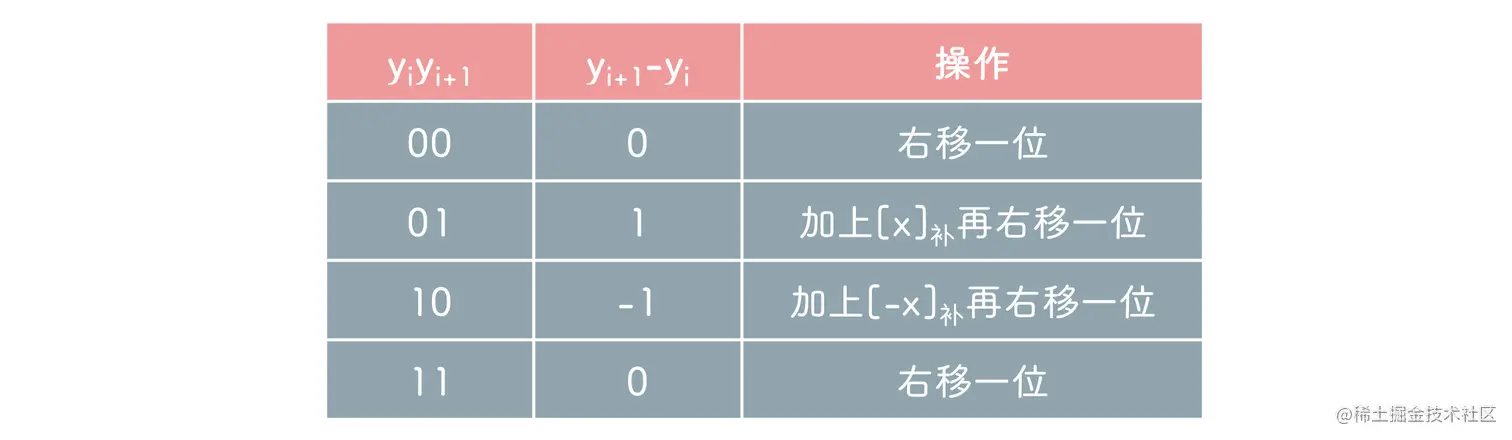
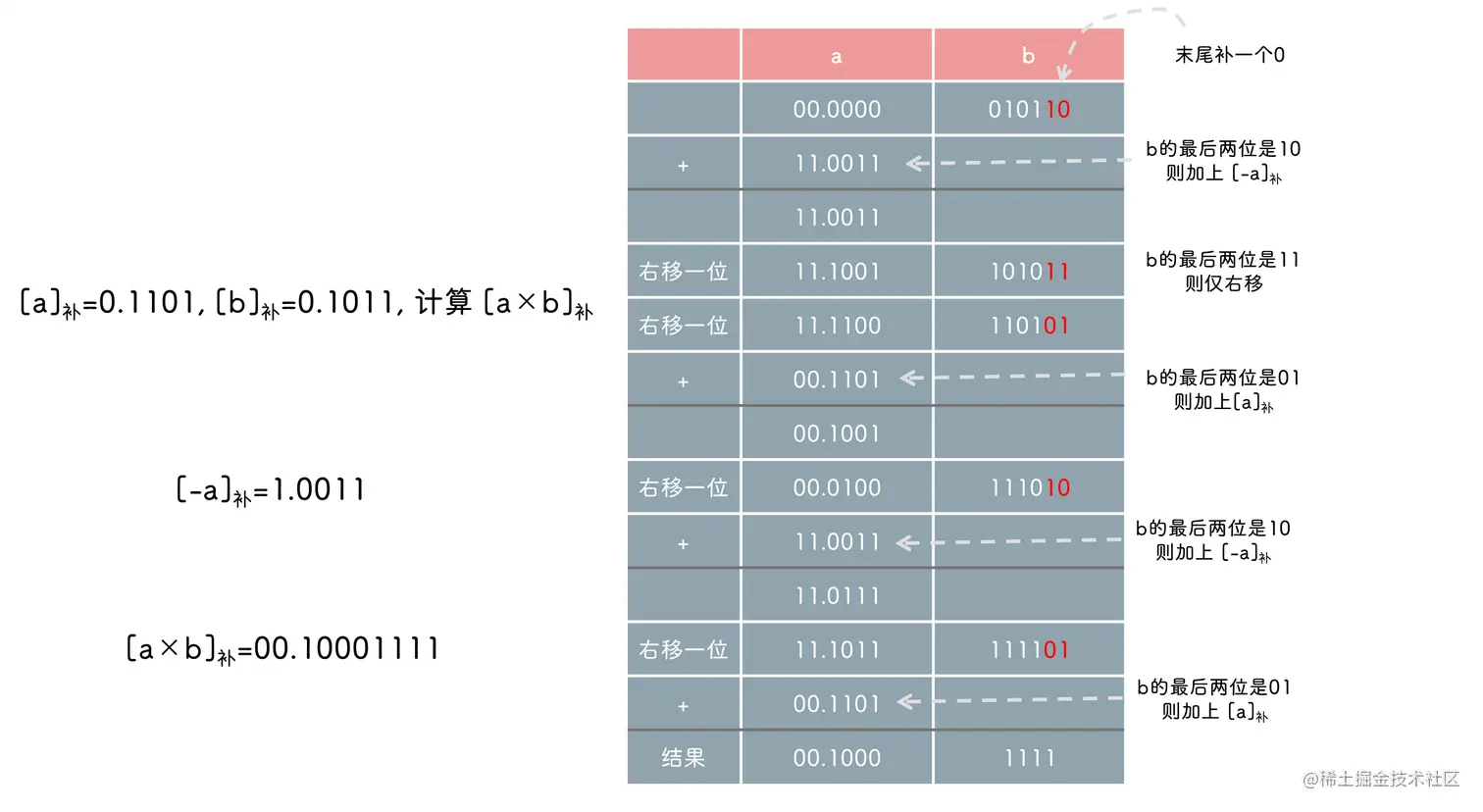
最后一步不需要右移, 由于 yi 会被用到两次, 因此乘数的位数是偶数还是奇数无影响
移位的次数仅与乘数 b 的数值位数有关
补码两位乘
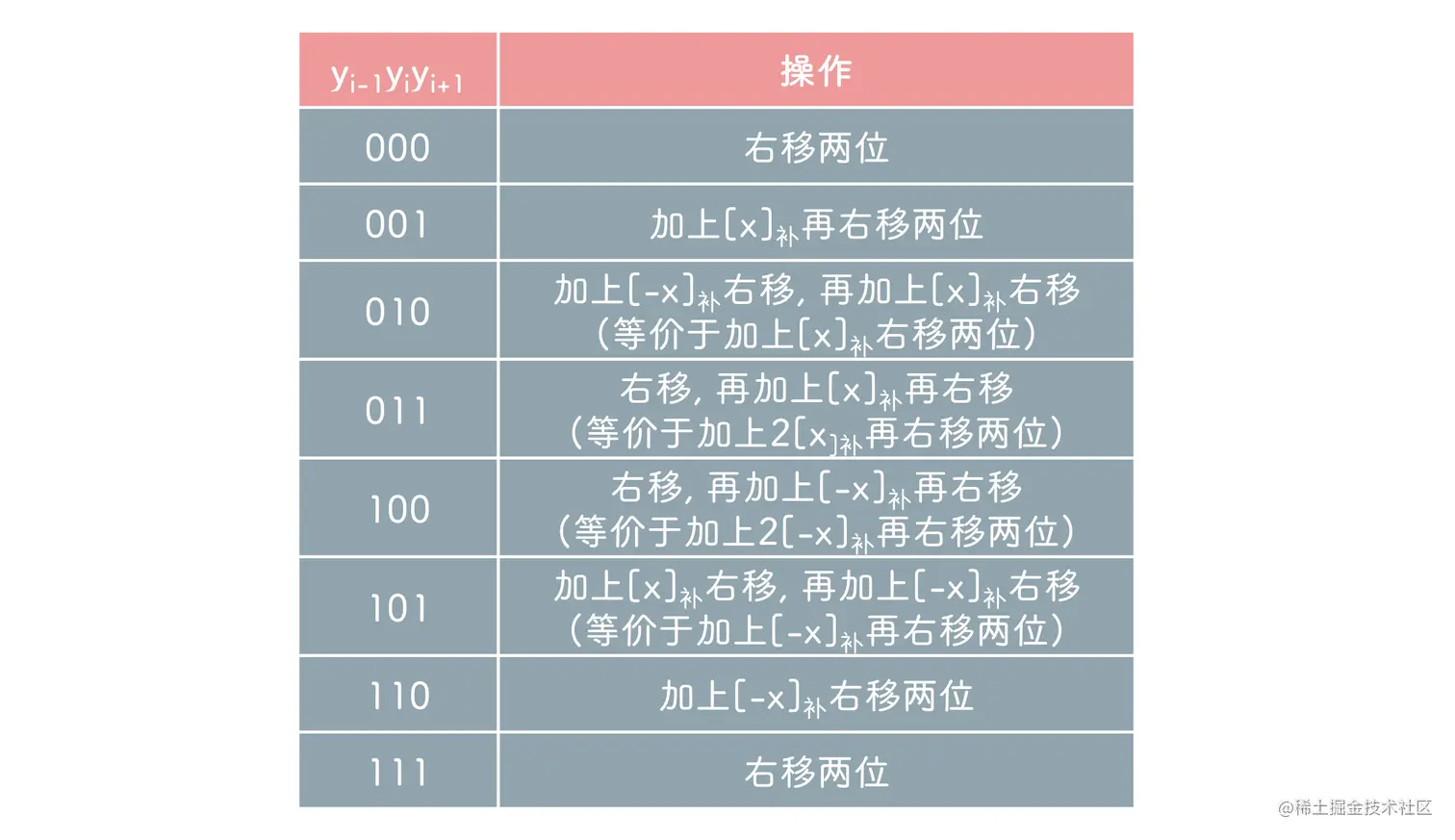
实际上 yi−1yiyi+1 可以分成两部分, 即先 yiyi+1 再 yi−1yi
因此 010 为先 10 (加上[−x]补右移一位) 然后 01 (加上[x]补右移一位)
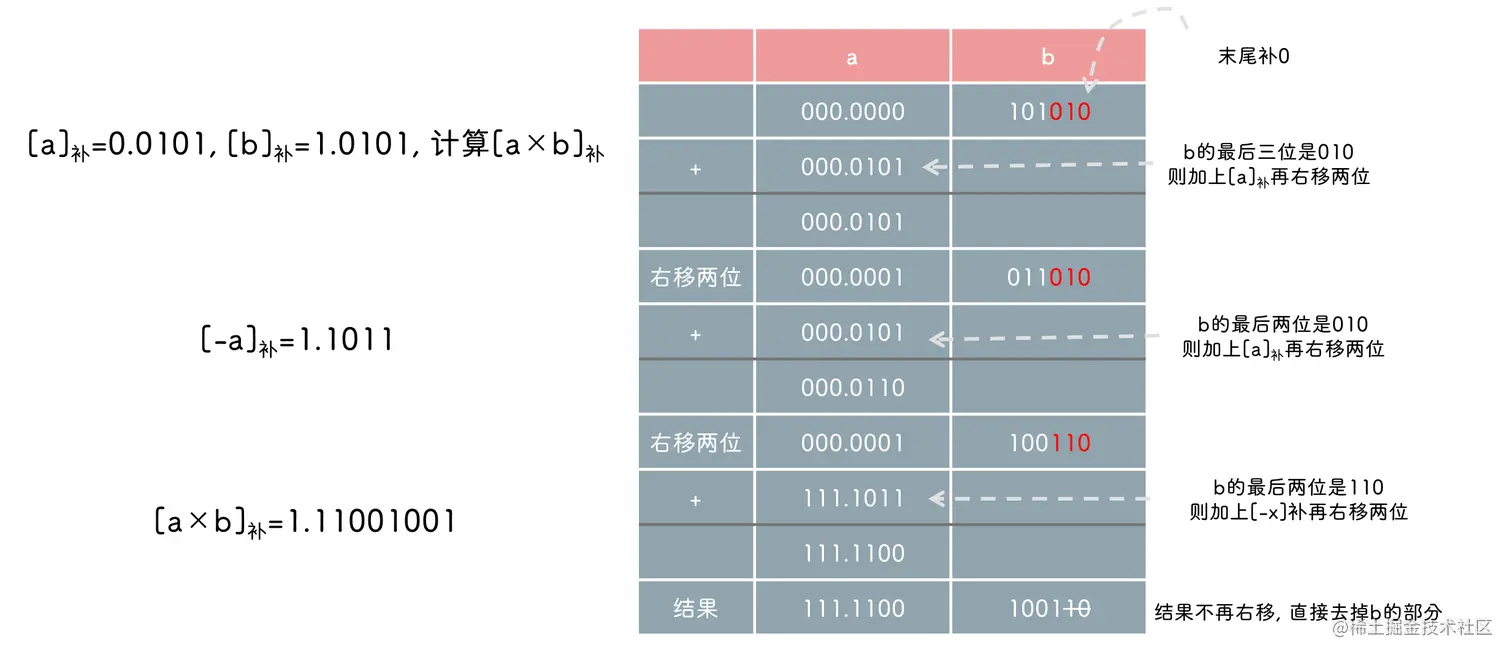
除法
规定: 商只除到和除数一样的位数
原码除法
恢复余数法
① 余数为负时加上 [∣b∣]补 恢复原来的余数, 然后商为 0 , 左移一位(相当于除法运算中不够除时看下一位), 继续加上 [−∣b∣]补
② 余数为正时商为 1, 左移一位, 加上 [−∣b∣]补
注意虽然是原码除法, 但是涉及到减法时用的还是补码(即减去除数绝对值, 实际上是加上除数绝对值负数的补码)
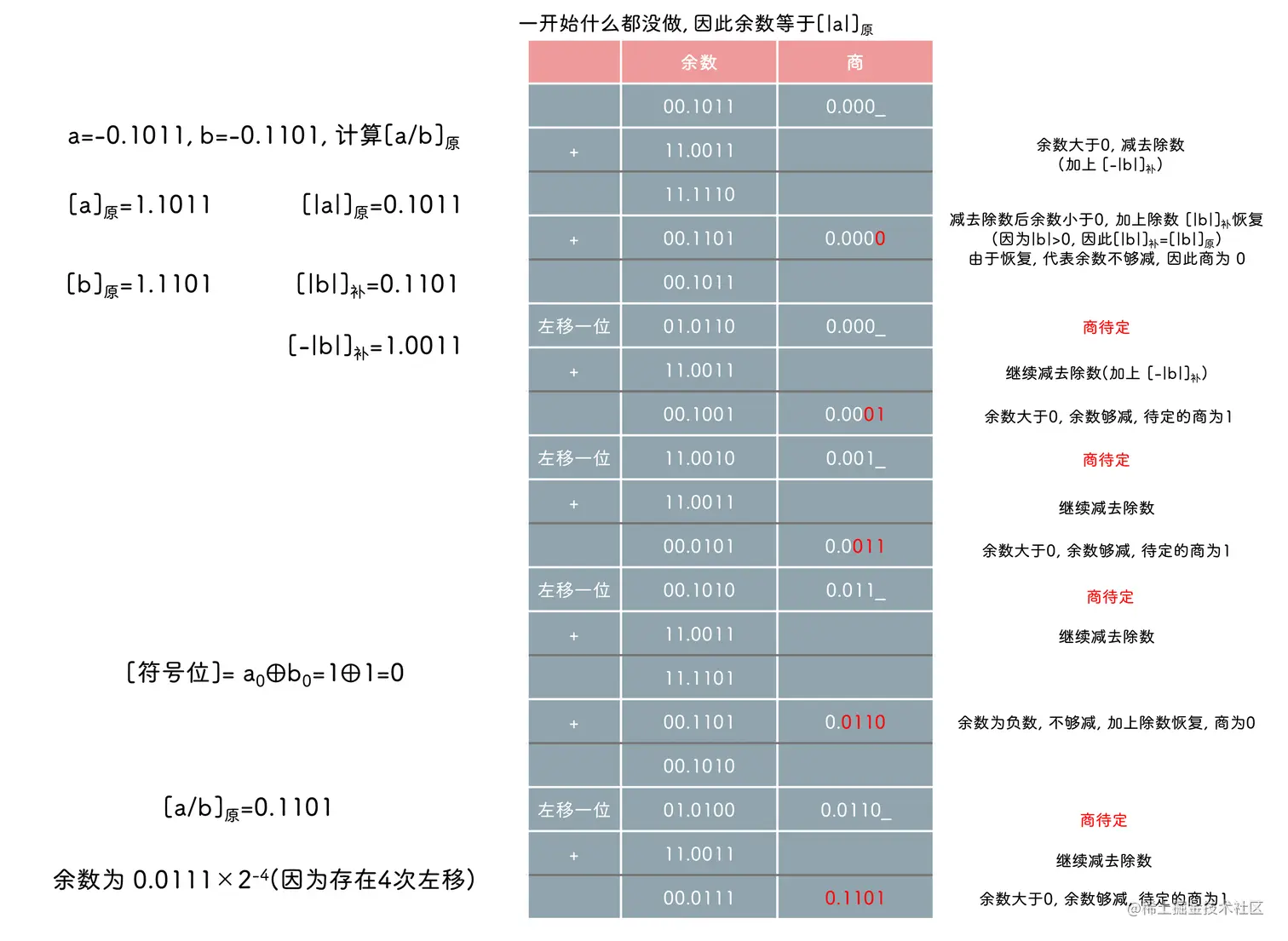
加减交替法
恢复余数法当余数小于 0 时加上 [∣b∣]补, 再左移一位, 继续加上 [−∣b∣]补 计算商, 其实可以合并到一起, 即先左移, 再加上 [∣b∣]补
可以通过下图理解(左移相当于 ×2 )

因此加减交替法为:
① 余数为负数, 左移一位, 商上0, 加上 [∣b∣]补
② 余数为正数, 左移一位, 商上1, 加上 [−∣b∣]补

补码除法
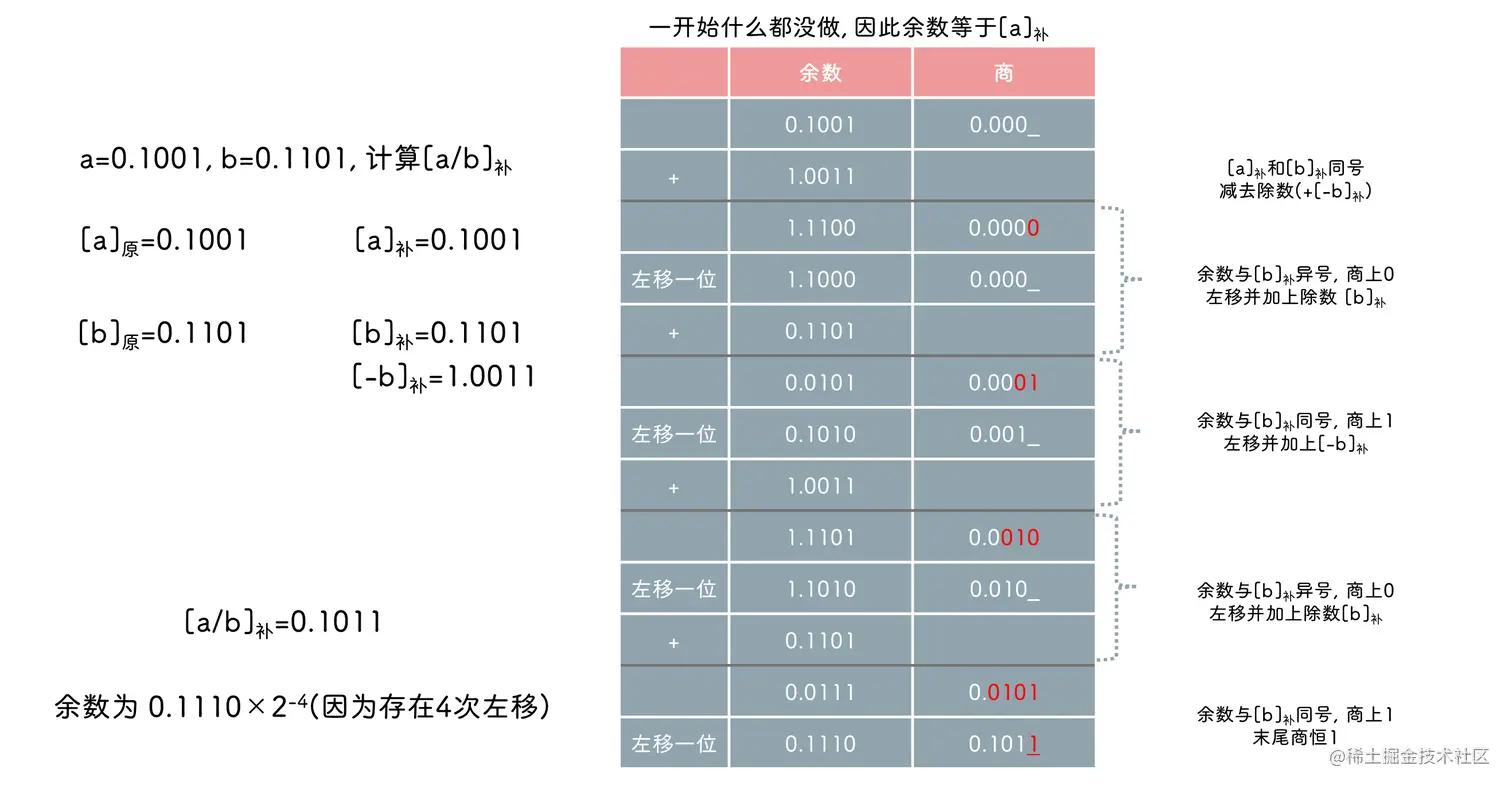
末尾商是否恒置 1 取决于精度要求