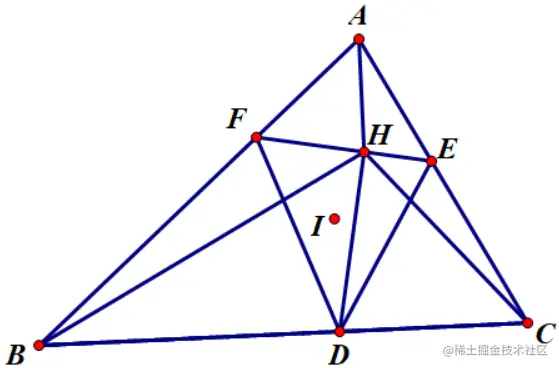
I为△ABC的内心,点 D,E,F 为 △ABC 内切圆的三个交点。HD⊥EF 于点 H。
若AH⊥BC ,证明: H 是△ABC的垂心。
大家可以先思考。
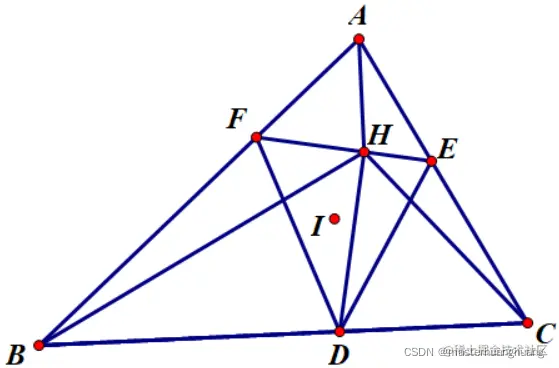 乍一看感觉没什么思路,因为 AH⊥BC 和之前的条件没什么关联,不太好处理。所以这引导我们要找到一个一般性结论,就是不一定满足 AH⊥BC 时恒成立的结论。
乍一看感觉没什么思路,因为 AH⊥BC 和之前的条件没什么关联,不太好处理。所以这引导我们要找到一个一般性结论,就是不一定满足 AH⊥BC 时恒成立的结论。
证:
我们发现: ∠BFH=∠CEH。又 H 是△ABC的垂心 ⇔∠FBH=∠ECH。
我们发现这里只需要证明△FBH∼△ECH⇔ECEF=HEFH。
接下来就是计算了。设 ∠B=α,∠C=β 。则EC∗sin2βEF∗sin2α=EDFD。ECEF=ED∗sin2αFD∗sin2β。
倒角得: ∠DFE= 90°−2β,∠DEF= 90°−2α。
∴HEFH=ED∗cos(∠DEF)FD∗cos(∠DFE)=ED∗sin2αFD∗sin2β=ECEF
证毕。
乍一看感觉没什么思路,因为 和之前的条件没什么关联,不太好处理。所以这引导我们要找到一个一般性结论,就是不一定满足 时恒成立的结论。