Day2 矩阵与变换
2D仿射变换
逆变换与组合变换
-
变换与逆变换对应矩阵与逆矩阵;
-
复杂的变换可以拆分成简单变换按顺序的组合(变换的顺序对应矩形乘法的逆序,详见例)。
-
例1: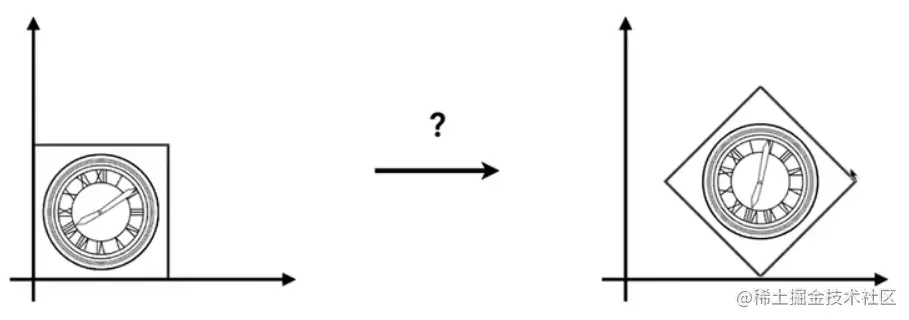 T(1,0)⋅R45⎣⎡xy1⎦⎤=⎣⎡100010101⎦⎤⎣⎡cos45°sin45°0−sin45°cos45°0001⎦⎤⎣⎡xy1⎦⎤
T(1,0)⋅R45⎣⎡xy1⎦⎤=⎣⎡100010101⎦⎤⎣⎡cos45°sin45°0−sin45°cos45°0001⎦⎤⎣⎡xy1⎦⎤
-
例2: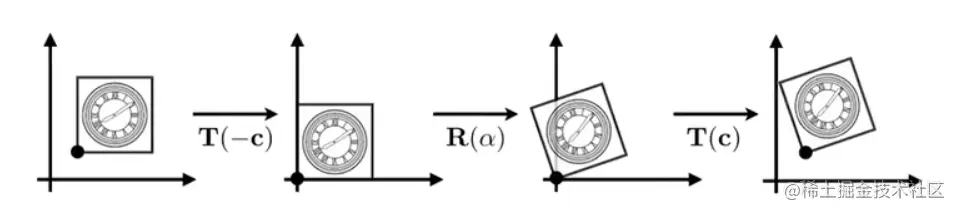 T(c)⋅R(α)⋅T(−c)
T(c)⋅R(α)⋅T(−c)
推广到3D
-
缩放:⎣⎡sx000sy000sz⎦⎤;
-
切片_沿X拉伸:⎣⎡100dy10dz01⎦⎤ ;
-
旋转:
- 绕x轴:⎣⎡1000cosθsinθ0−sinθcosθ⎦⎤ ;
- 绕y轴:⎣⎡cosθ0−sinθ010sinθ0cosθ⎦⎤ ;
- 绕z轴:⎣⎡cosθsinθ0−sinθcosθ0001⎦⎤ ;
-
平移+线性:⎣⎡adg0beh0cfi0txtytz1⎦⎤
Day3 观测变换——视图变换与投影变换
旋转的描述
欧拉角
(默认以原点旋转)将任意的旋转分解成绕x、y、z轴的旋转:
Rxyz(α,β,γ)=Rx(α)Ry(β)Rz(γ)
四元数
变换的过程
变换的目的——将三维物体映射到二维屏幕上
MVP变换
- 模型变换——model transformation:调整物体
- 视图变换——view transformation:调整相机
- 投影变换——projection transformation:建立映射
视图变换
需要调整的参数:
- 相机位置:原点——平移变换
- 相机朝向:z轴负方向——旋转变换
- 向上方向:y轴正方向——旋转变换
先平移后旋转即可
Mview=RviewTview
因为视图变换相机需要带动场景中的所有物体一起变换,维持相对位置不变,所以模型变换和相机变换经常一起进行,被称为模型视图变换
投影变换
- 正交投影——OrthographicProjection
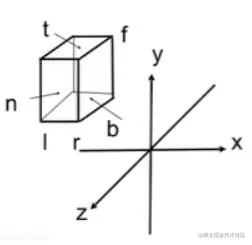
定义八方向参数:top,bottom,near,futher,left,right
先平移后缩放即可
Mortho=SorthoTortho
Mortho=⎣⎡r−l20000t−b20000n−f200001⎦⎤⎣⎡100001000010−2r+l−2t+b−2n+f1⎦⎤