VIO残差函数的构建以及IMU预积分和协方差传递本文已参与「新人创作礼」活动，一起开启掘金创作之路。基于滑动窗口的 V

本文已参与「新人创作礼」活动，一起开启掘金创作之路。

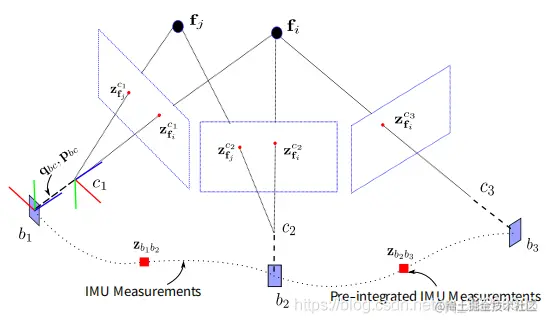
在这里插入图片描述

基于滑动窗口的 VIO Bundle Adjustment，为了节约计算量采用滑动窗口形式的 Bundle Adjustment，在 i 时刻，滑动窗口内待优化的系统状态量定义如下：

\chi = [X_n,X_{n+1},...,X_{n+N},\lambda{m},\lambda{m+1},...,\lambda{m+M}]

X_i=[p_{wb_i},q_{wb_i},v_i^w,b_a^{b_i},b_g^b{_i}],i \in [n,n+N]

其中:

$x_i$ 包含 $i$ 时刻 IMU 机体的在惯性坐标系中的位置，速度，姿态，以及 IMU 机体坐标系中的加速度和角速度的偏置量估计。
$m,n$ 分别是机体状态量，路标在滑动窗口里的起始时刻。
$N$ 滑动窗口中关键帧数量。
$M$ 是被滑动窗口内所有关键帧观测到的路标数量。
$\lambda$ 是逆深度。

IMU的真实值为 $w,a$ ，测量值为 $\tilde{w},\tilde{a}$ ，则有：

\tilde{w}^b=w^b+b^g+n^g

\tilde{a}^b=q_{bw}(a^w+g^w)+b^a+n^a

P(位置)，V(速度)，Q(位姿) 对时间的导数可写成：

\dot{p}_{wb_t}=v^w_t,\dot{v}^w_t=a^w_t,\dot{q}_{wb_t}=q_{wb_t}⊗ \begin{bmatrix} 0 \\ {1\over 2}w^{b_t} \\ \end{bmatrix}

从第 $i$ 时刻的 PVQ 对 IMU 的测量值进行积分得到第 $j$ 时刻的 PVQ：

p_{wb_j}=p_{wb_i}+v_i^w\Delta t +\iint_{t \in [i,j]}(q_{wb_t}a^{b_t}-g^w)\delta t^2

q_{wb_j}=\int_{t \in [i,j]}q_{wb_t}⊗ \begin{bmatrix} 0 \\ {1\over 2}w^{b_t} \\ \end{bmatrix}\delta t

每次 $q_{wb_t}$ 优化更新后，都需要重新进行积分，运算量较大。因此提出IMU预积分：

q_{wb_t}=q_{wb_i}⊗q_{b_ib_t}

那么，PVQ 积分公式中的积分项则变成相对于第 $i$ 时刻的姿态，而不是相对于世界坐标系的姿态：

p_{wb_j}=p_{wb_i}+v_i^w\Delta t +\iint_{t \in [i,j]}(q_{wb_t}a^{b_t}-g^w)\delta t^2 =p_{wb_i}+v_i^w\Delta t- {1\over 2}g^w \Delta t^2+\iint_{t \in [i,j]}(q_{wb_t}a^{b_t})\delta t^2

\implies \color{red}{p_{wb_j}=p_{wb_i}+v_i^w\Delta t- {1\over 2}g^w \delta t^2+q_{wb_i}\iint_{t \in [i,j]}(q_{b_ib_t}a^{b_t})\delta t^2}

v_i^w=v_i^w+\int_{t \in [i,j]}(q_{wb_t}a^{b_t}-g^w)\delta t \implies \color{red}{ v_i^w=v_i^w-g^w\Delta t+q_{wb_i}\int_{t \in [i,j]}(q_{b_ib_t}a^{b_t})\delta t}

q_{wb_j}=\int_{t \in [i,j]}q_{wb_t}⊗ \begin{bmatrix} 0 \\ {1\over 2}w^{b_t} \\ \end{bmatrix}\delta t \implies \color{red}{q_{wb_j}=q_{wb_i}\int_{t \in [i,j]}q_{b_ib_t}⊗ \begin{bmatrix} 0 \\ {1\over 2}w^{b_t} \\ \end{bmatrix}\delta t}

预积分量仅仅跟 IMU 测量值有关，它将一段时间内的 IMU 数据直接积分起来就得到了预积分量：

\alpha_{b_ib_j}=\iint_{t \in [i,j]}(q_{b_ib_t}a^{b_t})\delta t^2

\beta_{b_ib_j}=\int_{t \in [i,j]}(q_{b_ib_t}a^{b_t})\delta t

q_{b_ib_j}=\int_{t \in [i,j]}q_{b_ib_t}⊗ \begin{bmatrix} 0 \\ {1\over 2}w^{b_t} \\ \end{bmatrix}\delta t

将 $\alpha_{b_ib_j},\beta_{b_ib_j},q_{b_ib_j}$ 代入整理可得到最终的PVQ积分公式：

\begin{bmatrix} p_{wb_j}\\v_j^w\\q_{wb_j}\\b_j^a\\b_j^g\\ \end{bmatrix}=\begin{bmatrix} p_{wb_i}+v_i^w\Delta t- {1\over 2}g^w \Delta t^2+q_{wb_i}\color{red}{\alpha_{b_ib_j}}\\v_i^w-g^w\Delta t+q_{wb_i}\color{red}{\beta_{b_ib_j}} \\q_{wb_i}\color{red}{q_{b_ib_j}}\\b_i^a\\b_i^g\\ \end{bmatrix}

预积分误差：一段时间内 IMU 构建的预积分量作为测量值，对两时刻之间的状态量进行约束

\begin{bmatrix} r_p\\r_q\\r_v\\r_{ba}\\r_{bg}\\ \end{bmatrix}=\begin{bmatrix} p_{wb_j} - p_{wb_i}-v_i^w\Delta t+ {1\over 2}g^w \Delta t^2-q_{wb_i}\color{red}{\alpha_{b_ib_j}}\\ 2[{\color{red}{q_{b_jb_i}}}⊗(q_{b_iw} ⊗ q_{wb_j})]_{xyz} \\v_j^w - v_i^w+g^w\Delta t-q_{wb_i}\color{red}{\beta_{b_ib_j}} \\b_j^a-b_i^a\\b_j^g-b_i^g\\ \end{bmatrix}=\begin{bmatrix} q_{b_iw}(p_{wb_j} - p_{wb_i}-v_i^w\Delta t+ {1\over 2}g^w \Delta t^2)-\color{red}{\alpha_{b_ib_j}}\\ 2[{\color{red}{q_{b_jb_i}}}⊗(q_{b_iw} ⊗ q_{wb_j})]_{xyz} \\q_{b_iw}(v_j^w - v_i^w+g^w\Delta t)-\color{red}{\beta_{b_ib_j}} \\b_j^a-b_i^a\\b_j^g-b_i^g\\ \end{bmatrix}

上面误差中位移，速度，偏置都是直接相减得到。第二项是关于四元数的旋转误差，其中 $[\cdot]_{xyz}$ 表示只取四元数的虚部 $(x, y, z)$ 组成的三维向量。

预积分的离散形式 以上是预积分的连续形式，也可以使用离散形式，这里使用 $mid-point$ 方法，即两个相邻时刻 $k$ 到 $k+1$ 的位姿是用两个时刻的测量值 $a, ω$ 的平均值来计算：

w={1 \over 2}((w^{b_k}-b_k^g)+(w^{b_{k+1}}-b_k^g))\

a={1\over 2}(q_{b_ib_k}(a^{b_k}-b_k^a)+q_{b_ib_{k+1}}(a^{b_{k+1}}-b_k^a))

预积分量的方差 协方差传递性质：在一个线性系统中，已知一个变量 $y = Ax, x ∈ \mathcal N (0, Σ_x)$ , 则有 $Σ_y = AΣ_xA^⊤$

Σ_y = E((Ax)(Ax)^⊤) = E(Axx^⊤A^⊤) = AΣ_xA^⊤

要推导预积分量的协方差，我们需要知道 imu 噪声和预积分量之间的线性递推关系。

假设已知了相邻时刻误差的线性传递方程：

η_{ik} = {\color{red}F_{k−1}η_{ik−1}} + {\color{blue}G_{k−1}n_{k−1}}

比如：状态量误差为 $η_{ik} = [δθ_{ik}, δv_{ik}, δp_{ik}]$ ，测量噪声为 $n_k = [n^g_k, n^a_k]$ 。误差的传递由两部分组成：1.当前时刻的误差传递给下一时刻，2.当前时刻测量噪声传递给下一时刻。协方差矩阵可以通过递推 $Σ_y = AΣ_xA^⊤$ 计算得到：

Σ_{ik} = {\color{red} F_{k−1}Σ_{ik−1}F^⊤_{k−1}} +{\color{blue} G_{k−1}Σ_nG^⊤_{k−1}}

其中， $Σ_n$ 是测量噪声的协方差矩阵，方差从 $i$ 时刻开始进行递推， $Σ_{ii} = 0$ 。

状态误差线性递推公式的推导(线性化) 协方差传递性质只对于线性化系统，通常对于状态量之间的递推关系是非线性的方程如 $x_k = f(x_{k−1}, u_{k−1})$ ，其中状态量为 $x，u$ 为系统的输入量。

我们可以用两种方法来推导状态误差传递的线性递推关系：

一种是基于一阶泰勒展开的误差递推方程（应用于 EKF 的协方差预测）。令状态量为 $x = \hat{x} + δx$ ，其中，真值为 $\hat{x}$ ，误差为 $δx$ 。另外，输入量 $u$ 的噪声为 $n$ 。非线性系统 $x_k = f(x_{k−1}, u_{k−1})$ 方程进行一阶泰勒展开有：

x_k = f(x_{k−1}, u_{k−1})

\hat{x}_k +δx_k= f(\hat{x}_{k−1}+δx_{k-1}, \hat{u}_{k−1}+n_{k-1})

\hat{x}_k +δx_k= f(\hat{x}_{k−1}, \hat{u}_{k−1})+Fδx_{k-1}+Gn_{k-1}

{\color{red}δx_k= Fδx_{k-1}+Gn_{k-1}}

其中，F 是状态量 $x_k$ 对状态量 $x_{k−1}$ 的雅克比矩阵，G 是状态量 $x_k$ 对输入量 $u_{k−1}$ 的雅克比矩阵。 2. 一种是基于误差随时间变化的递推方程。如果我们能够推导状态误差随时间变化的导数关系，比如： $δ\dot{x} = Aδx + Bn$ 则误差状态的传递方程为：

δx_k = δx_{k−1} + δ\dot{x}_{k−1}∆t → δx_k = (I + A∆t)δx_{k−1} + B∆tn_{k−1}

这两种推导方式的可以看出有： $F = I + A∆t, G = B∆t$

回顾预积分(离散形式)的误差递推公式，将测量噪声也考虑进模型：

w={1 \over 2}((w^{b_k}+ {\color{red}n_k^g}-b_k^g)+(w^{b_{k+1}}+ {\color{red}n_{k+1}^g}-b_k^g))

a={1\over 2}(q_{b_ib_k}(a^{b_k}+ {\color{red}n_k^a}-b_k^a)+q_{b_ib_{k+1}}(a^{b_{k+1}}+ {\color{red}n_{k+1}^a}-b_k^a))

确定误差传递的状态量，噪声量，然后开始构建传递方程。用前面一阶泰勒展开的推导方式，我们能推导出如下的形式：

\begin{bmatrix} δα_{b_{k+1}b′_{k+1}} \\ δθ_{b_{k+1}b′_{k+1}} \\ δβ_{b_{k+1}b′_{k+1}} \\δb^a_{k+1}\\ δb^g_{k+1}\\ \end{bmatrix}=F\begin{bmatrix} δα_{b_{k}b′_{k}} \\ δθ_{b_{k}b′_{k}} \\ δβ_{b_{k}b′_{k}} \\δb^a_{k}\\ δb^g_{k}\\ \end{bmatrix}+G\begin{bmatrix} n^a_k\\n^g_k\\n^a_{k+1}\\n^g_{k+1}\\n_{b^a_a}\\n_{b^g_k}\\ \end{bmatrix}

F, G 为两个时刻间的协方差传递矩阵。

对VIO残差函数的构建的理解：

对于 $T$ 时刻的状态量，如位置、速度、变换、偏置。可通过IMU测量值 $(w,a)$ 积分得到 $T+1$ 时刻的状态。

由于状态量中的参考系都在全局坐标系下，对于每一时刻的状态优化完成之后，需要重新积分得到下一时刻的状态，因此提出预积分的概念，将积分转换成相对于上一时刻的量。

通过对上一时刻 $T$ 预积分得到当前时刻 $T+1$ 的状态作为测量值，通过当前时刻的真实值作为约束，得到残差函数。

以上过程再考虑到噪声、误差的影响，通过线性系统的协方差传递性质，将状态量之间的递推关系线性化，即利用F,G，考虑到上一时刻的误差以及当前时刻的观测误差。最终所得到的残差函数即为，上一时刻的预积分加上传递误差，与当前时刻的约束。