在SLAM中非线性最小二乘问题利用舒尔补简化求解增量

秃头队长
305 阅读2分钟

本文已参与「新人创作礼」活动，一起开启掘金创作之路。

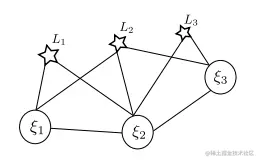
高斯牛顿求解流程 有如下最小二乘系统，对应的模型如下所示：

在这里插入图片描述

ξ=argminξ12∑i∥ri∥∑i2\xi = \underset{\xi}{argmin}{1\over 2}\sum_i\lVert r_i\rVert^2_{\sum_i}

对上式展开求导，令其导数为零，可得到Hx=bHx=b的形式，上式对应的高斯牛顿求解 normal equation：

J⊤Σ−1J⏟H or Aδξ=−J⊤Σ−1r⏟b\underbrace{J^\topΣ^{-1}J}_{H \,or \,A}δξ=\underbrace{-J^\topΣ^{-1}r}_{b}

如果HH可逆，则可以直接求解Δx=−H−1b\Delta x=-H^{-1}b，但其计算量较大。在另一篇关于舒尔补的博客中可以知道，舒尔补从概率上可以加速问题求解，利用SLAM问题的稀疏性。

例如某单目BA问题，其信息矩阵如下所使：

在这里插入图片描述

[HppHplHlpHll][Δxp∗Δxl∗]=[−bp−bl]\begin{bmatrix} H_{pp} & H_{pl} \\ H_{lp} & H_{ll} \\ \end{bmatrix} \begin{bmatrix} \Delta x^*_p \\\Delta x^*_l \\ \end{bmatrix} =\begin{bmatrix} -b_p\\-b_l \\ \end{bmatrix}

其中HppH_{pp}代表相机pose之间的信息矩阵，HplH_{pl}代表相机与路标点之间的信息矩阵，HllH_{ll}代表路标点之间的信息矩阵。 接下来利用如下舒尔补的操作，使上式信息矩阵变成下三角矩阵。

[I−BD−10I][ABCD]=[A−BD−1C0C D]\begin{bmatrix} I &-BD^{-1} \\ 0&I\\ \end{bmatrix}\begin{bmatrix} A&B \\C&D\\ \end{bmatrix} = \begin{bmatrix} A-BD^{-1}C&0 \\C&\ D \\ \end{bmatrix}
[I−HplHll−10I][HppHplHlpHll]=[Hpp−HplHll−1Hlp0HlpHll]\begin{bmatrix} I & -H_{pl}H^{-1}_{ll}\\ 0 & I\\ \end{bmatrix}\begin{bmatrix} H_{pp} & H_{pl} \\ H_{lp} & H_{ll} \\ \end{bmatrix} = \begin{bmatrix}H_{pp}-H_{pl}H_{ll}^{-1}H_{lp} & 0 \\ H_{lp} & H_{ll} \\ \end{bmatrix}
⇓带入到信息矩阵中\Downarrow 带入到信息矩阵中
[I−HplHll−10I][HppHplHlpHll][Δxp∗Δxl∗]=[I−HplHll−10I][−bp−bl]\begin{bmatrix} I & -H_{pl}H^{-1}_{ll}\\ 0 & I\\ \end{bmatrix}\begin{bmatrix} H_{pp} & H_{pl} \\ H_{lp} & H_{ll} \\ \end{bmatrix}\begin{bmatrix} \Delta x^*_p \\\Delta x^*_l \\ \end{bmatrix} =\begin{bmatrix} I & -H_{pl}H^{-1}_{ll}\\ 0 & I\\ \end{bmatrix}\begin{bmatrix} -b_p\\-b_l \\ \end{bmatrix}
  ⟹  [Hpp−HplHll−1Hlp0HlpHll][Δxp∗Δxl∗]=[I−HplHll−10I][−bp−bl]\implies \begin{bmatrix}H_{pp}-H_{pl}H_{ll}^{-1}H_{lp} & 0 \\ H_{lp} & H_{ll} \\ \end{bmatrix}\begin{bmatrix} \Delta x^*_p \\\Delta x^*_l \\ \end{bmatrix}=\begin{bmatrix} I & -H_{pl}H^{-1}_{ll}\\ 0 & I\\ \end{bmatrix}\begin{bmatrix} -b_p\\-b_l \\ \end{bmatrix}

从而得到：

(Hpp−HplHll−1Hlp)Δxp∗=−bp+HplHll−1bl(H_{pp}-H_{pl}H_{ll}^{-1}H_{lp}) \Delta x^*_p = -b_p+ H_{pl}H^{-1}_{ll}b_l

求得Δxp∗\Delta x^*_p后再计算Δxl∗\Delta x^*_l：HllΔxl∗=−bl−Hpl⊤Δxp∗H_{ll}\Delta x^*_l=-b_l-H^{\top}_{pl}\Delta x^*_p

在SLAM中整个solver流程可以总结为： 利用IMU构建残差，重投影误差构建姿态和路标点关系。 构建误差函数rij→  r_{ij}\to \;计算雅可比Jij→  (H+λI)δx=b→  J_{ij}\to \;(H+\lambda I)δx=b \to\;利用舒尔补简化求解 →  \to \;求解出增量Δx\Delta x作用到之前变量上，更新残差、更新雅可比，不断迭代。

但是在实际情况中，信息矩阵H并不满秩，可使用LM算法，H=H+λIH=H+\lambda I，加阻尼因子使得系统满秩，但是求解的结果可能会往零空间变化。简单来说就是，在残差构建的过程中，得到的是相机pose与路标点landmark之间或者相机之间的相对关系，并没有建立与世界坐标系之间的绝对关系，因此可能因为第一帧的漂移导致整个系统发生漂移。

另一种方法是添加先验，增加系统的可观性。例如约束第一帧相机的pose被固定在(0,0,0)(0,0,0)原点，即先验信息。在g2o turorial中对第一个pose的信息矩阵加上单位阵，H[11]+=IH_{[11]}+=I，存在(H[11]+I)Δx=b(H_{[11]}+I)\Delta x=b，即IΔx=0I\Delta x=0，使得第一帧的pose不动。但是尺度依然无法确定，常用的办法可以再固定一个landmark，也可以再固定一个相机pose，固定其相对的位移。

优化过程中处理 H 自由度的不同操作方式可参考博客对《On the comparison of gauge freedom handling in optimization-based visual-inertial state estimation》。

avatar
文章
阅读
粉丝