本文已参与「新人创作礼」活动，一起开启掘金创作之路。

CTL和LTL的区别：

• CLT明确允许对路径使用量词，比LTL有更强的表达能力
• 但CTL不允许像LTL那样，通过用公式描述来选择一个路径范围，在这方面LTL更有表达能力。
• 比如：“对所有这样的路径，沿该路径有p的话，也有q”，用LTL表示为$Fp \to Fq$
• 但由于收到所有$F$必须伴随着一个$A$或$E$使用的约束，用CTL写成$Fp \to Fq$是不可能的
  • 如果CTL写成$AFp \to AFq$，则表示为“如果沿着所有路径有p，那么沿着所有路径也有q"；
  • 如果CTL写成$AG(p \to AF q)$，则表示为“所有路径延伸到$p$最终会遇到$q$”，与$Fp \to Fq$的意义还是不相同。
• 说明LTL公式$FGp$和CTL公式$AFAGp$不等价的范例： 下图的模型中，$FGp$是满足的，$AFAGp$是不满足的

LTL公式$XFp$、LTL公式$FXp$、CTL公式$AXAFp$是等价的，但不与CTL公式$AFAXp$等价

CTL*、CTL、LTL的关系：

• CTL*公式将LTL和CTL的表达能力结合，并去除了CTL对每个时态算子（X，U，F，G）必须与唯一路径量词（A，E）伴随使用的约束而得到的一种逻辑。
• 表达能力之间的关系
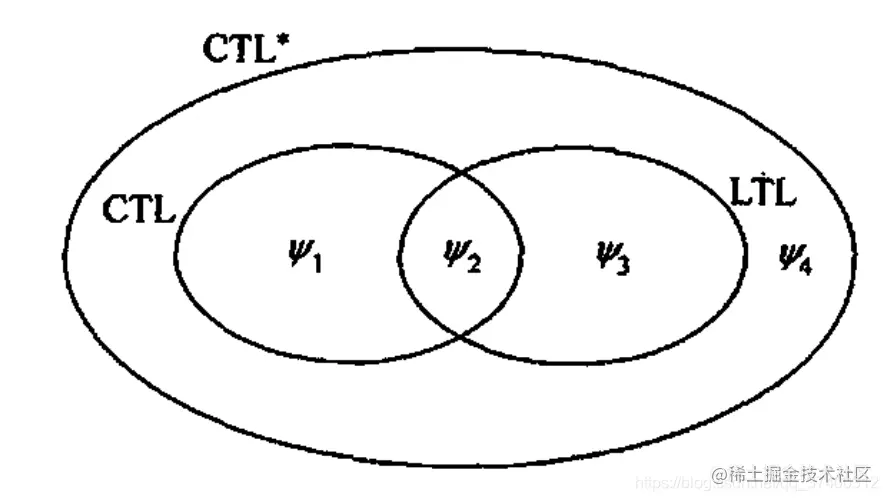
  • 在CTL中但不在LTL中：$\psi_1 \overset{def}{ = } AGEFp$，表示无论到哪里，我们总可以到达一个使p为真的状态，例如在协议中寻找死锁。
  • 在LTL中但不在CTL中：$\psi_3 \overset{def}{ = } A[GFp \to Fq]$，表示如果沿该路径有无限多p，则q出现一次。
  • 在LTL中和CTL中：$\psi_2 \overset{def}{ = } AG[p \to AFq]$在CTL中，或者$G(p \to Fq)$在LTL中，表示任何p最终都跟着一个q
  • 在CTL*中，但不在CTL和LTL中：$\psi_4 \overset{def}{ = } E[GFp]$，表示存在一条有限多p的路径
  • 在

CTL*公式

状态公式，用状态来赋值： $\phi :: = \top | p | (\neg \phi) | (\phi \wedge \phi) | A[\alpha] |E (\alpha)$ 路径公式，沿着路径赋值： $\alpha :: = \phi | (\neg \alpha) | (\alpha \wedge \alpha ) | (\alpha U \alpha)|(G \alpha) | (F \alpha) | (X \alpha)$ 范例：

• $A[(p U r) \vee (q U r)]$
• $A[X p \vee XX p]$
• $E [GFp]$

LTL中的过去算子

• LTL中的时态算子$X,U,F$等都是参考未来的算子，有时我们可能需要一个参考过去的算子，我们称之为过去算子。
• 过去算子：
  • $Y$表示昨天，与$X$对立
  • $S$表示自从，与$U$对立
  • $O$表示i曾经，与$F$对立
  • $H$表示历史地，与$G$对立
• 例如：“只要q出现，那么过去已经有某一个p出现过了”可以表示为$G(q \to Op)$

• NuSMVz支持LTL中的过去算子，但不支持CTL中的过去算子（例如AX，ES等）
• 过去算子并不能增加LTL的表达能力，他们只是可以等价地写为不带过去算子地公式