人工智能(AI)的广泛方法是在计算环境中复制人类的理性能力。评估人工智能能力的最好方法之一是看他们是否能在游戏中击败人类。
鉴于国际象棋和围棋的复杂性,数独应该是小菜一碟。当然,在某些情况下,蛋糕是个谎言。 虽然人工智能可以利用理性来选择获胜的策略,但人类的一点聪明才智和编码逻辑(使用一种叫做回溯的技术)也同样可以发挥作用。
在这篇文章中,你将
- 创建一个包含我们的任务所需的所有包的Python环境
- 确定我们的方法。蛮力与机器学习
- 导入Kaggle的数独谜题数据集
- 测试 "蛮力 "方法
- 建立一个算法来解决数独谜题
- 得出一些关于人工智能是否比人类更有效地解决数独问题的结论
本文中使用的所有代码都可以在我的 GitLab仓库中找到 。都准备好了吗?我们开始吧。
1-在你开始之前。安装Sudoku Solver Python环境
为了跟上本文的代码,你可以下载并安装我们预建的数独解算器环境,其中包含Python 3.9版本和本文中使用的软件包。
为了下载这个随时可用的Python环境,你需要创建一个ActiveState Platform账户。只需使用你的GitHub凭证或你的电子邮件地址来注册。注册很简单,它可以为你解锁ActiveState平台的许多好处
或者你也可以使用我们的 State工具 来安装这个运行时环境。
对于Windows用户,在CMD提示下运行以下程序,就可以自动下载并安装我们的CLI、State工具以及Sudoku Solver到 一个虚拟环境中。
powershell -Command "& $([scriptblock]::Create((New-Object Net.WebClient).DownloadString('https://platform.activestate.com/dl/cli/install.ps1'))) -activate-default Pizza-Team/SudokuSolver"
对于Linux用户,运行下面的程序可以自动下载并安装我们的CLI、状态工具和 数独解算器到 虚拟环境中。
sh <(curl -q https://platform.activestate.com/dl/cli/install.sh) --activate-default Pizza-Team/SudokuSolver
用Python解决数独问题的两种方法
一个数独谜题由一个9乘9的网格组成,每个单元格包含一个1到9的数字。9乘9的网格被划分为9个子网格,这些子网格由第一、中间和最后3列以及第一、中间和最后3行的交叉点定义。该谜题的答案必须满足以下条件。
- 每一行必须包含1到9,没有重复的内容。
- 每一列必须包含1到9,没有重复的内容。
- 每个子网格必须包含1到9,没有重复。
当然,谜题中的一些单元格是空的,我们的目标是填入空的单元格,直到满足条件。举例来说。
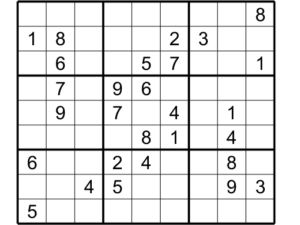
接近问题
在 "深蓝 "的案例中,程序被设计为评估每个国际象棋棋子在每个回合中每个可能位置的相对风险。这在很大程度上 依赖于蛮力 计算,这需要大量的时间,大量的计算能力,或者两者都需要。
国际象棋的复杂性可以通过计算棋盘位置的总数来量化,这大约相当于1047种 可能性。另一方面,围棋有大约10170种 不同的配置。这使得使用蛮力算法来下围棋是不可行的,所以AlphaGo使用机器学习(ML)和树形算法的组合来进行游戏中的决策。
数独的复杂性取决于网格中空单元的数量。如果81个单元格中有41个是空的,每个单元格可以取1到9的值,就有941种 可能的配置。这使得数独的复杂度类似于国际象棋,其中蛮力算法是可以实现的。这将是我们使用Python解决数独游戏的方法。
3-数独数据集
幸运的是,Kaggle有一个公开的900万道数独谜题及其解法的数据集,可以在这里找到。在下载了_.csv_文件之后,我们可以通过运行来导入谜题。
import numpy as np
我只导入了前100个谜题,但可以根据需要随意导入更多的谜题。数据框架的每一行都包含一个谜题和相应的答案。它们看起来应该是这样的。
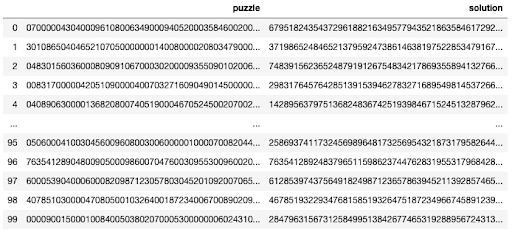
为了使每道谜题在标准的9乘9网格中可视化,而不是81个字符的字符串,我们可以写一个函数来重新塑造它。
def
再来看看第一道谜题。
sudoku_df = shape(sudoku_df)

零代表我们需要填充的空单元格。解决方案看起来是这样的。
sudoku_df.iloc[

在我们解释如何解决这个谜题之前,我们应该实现数独的三个条件,以验证任何提议的解决方案实际上是一个解决方案。这可以通过以下函数来实现。
def
对于每个问题的解决方案,我们都要检查一下。
- 每一行包含所有的数字1到9
- 每一列包含所有1到9的数字
- 每个子网格包含所有的数字1到9
如果它们都被检查出来,该函数就输出 "真";如果不是,就输出 "假"。你可以用第一道题的答案来试试。
4-用蛮力解决数独问题
要建立一个解决任何数独谜题的算法,我们实际上只需要解决一个单一的谜题。然后,我们可以将每个函数泛化,使任何谜题都可以作为输入。让我们来看看上面的谜题,它有44个空单元格。
len(np.where(sudoku_df.iloc[
如果我们假设每个单元格可以有9个值,这意味着有大约1041个 可能的解决方案。
"{:.2e}"
然而,这还没有考虑到已经被填入的单元格的数值。利用这些数值(以及我们最初的三个条件--数独规则),我们可以算出每个单元格中允许有哪些数值。
def
在上面的代码中,函数。
- 扫描每个单元格,确定该单元格的行、列和子网格中已经存在的值。
- 从我们的1到9的值列表中删除已知的值(如果单元格已经被填满,唯一可能的值就是已经给出的值)。
- 输出是每个单元格的可能值的列表。
现在我们可以在第一道题上运行这个函数,如下所示。
puzzle_values = determineValues(sudoku_df.iloc[

所以,从左到右,从上到下。
- 第一个单元格的可能数值为1,2,5,或6。
- 第二个单元格已经有一个7。
- 第三个单元格可能有1,5,6,或9。
以此类推。列表的总长度应该是81行,这相当于单元格的总数(9×9)。现在我们知道了每个单元格的可能数值,这限制了谜题的复杂性。现在可能性的数量是。
combinations =
这还是相当高的,但比以前好得多。我 们可以写一个函数来生成所有1.25e19的9乘9矩阵,然后用我们的 checkPuzzle 函数来扫描每个矩阵,直到找到答案。尽管这样的练习很简单,但这一过程将是计算密集型的。为了了解它的可行性,我们可以加入一个计时器,只扫描一部分的可能性来确定大致的总时间。这个函数看起来会是这样的。
def
注意,我以这种方式合并了前三行、中间三行和最后三行,因为 numpy 不允许有81维的数组。我在104次 迭代 后停止了该函数 ,并将迭代率投射到潜在解决方案的总数量上。
bruteForce_check(puzzle_values)
这是个相当长的时间!显然,这种方法并不理想。取而代之的是,我们将实现一种叫做 Backtracking的东西 。
5-用回溯法解决数独问题
我们的蛮力方法包括确定每个单元格的可能值,生成所有可能的9乘9的网格,并对每个网格进行扫描。一个更好的方法是选择一个单元格开始,然后。
- 从我们的列表中插入一个数字,并检查其有效性条件。
- 如果条件有效,就移到一个新的单元格。
- 如果条件是无效的,就在列表中挑选下一个数字。
- 重复这个过程,直到单元格列表中的所有数值都没有通过有效性检查或所有单元格都被填满。
- 如果该单元格的值已经用完,则移到前一个单元格,挑选一个不同的值,然后重复。
通过这种方式,我们在构建解决方案时检查每个单元格的有效性,并在某个值不符合要求时拒绝。为了在Python中实现这一点,我们首先需要一个函数来有效地检查与当前单元对应的子网格(这在后面会很有用)。
def
理论上说,函数通过网格的路径和每个单元格的值的顺序都会影响到找到一个解决方案的总时间。然而,我们没有办法事先知道哪条路径或顺序是最好的。因此,我们将从左到右、从上到下扫描空单元格,我们也将从最小到最大扫描数值。
我将定义几个实用变量来跟踪。
- 当前单元格(计数
- 谜题的解题状态(解)。
- 每个单元格的现在和过去的数值指数的字典(num 和 dic
一旦最后一个空单元格被填入一个有效的值,整个矩阵就会被 checkPuzzle 函数进行双重检查 。
def
上述函数。
- 检查每个行、列和子网格的有效性。
- 如果失败,则 选择_puzzle_value[r,c]_中的下一个值
- 如果通过,该值将被分配给该单元格,我们将继续下一个单元格(并且 计数 增加1
- 如果某个单元格的值都没有通过(即 执行了 else )。
- 该单元格的值被重置为0
- 通过潜在值的循环被重置
- 我们回到上一个单元格(并且 _计数_减少 1)。
为了运行第一道题的代码,我们运行。
solve(sudoku_df.iloc[

这比之前的蛮力方法快多了!
结论。Python解决数独的速度比人类快
虽然人工智能和机器学习在Python社区得到了很多人的喜爱,但它们并不总是解决问题的最佳方法。另一方面,如果不能使用超级计算机,用蛮力解决问题也是不可行的。
解决数独问题的方法介于两者之间:太复杂了,无法用蛮力解决(人类的效率要高得多),但如果我们对如何去解决它很聪明的话,就不会这样。通过添加一些回溯逻辑,我们可以测试出每个单元格的值,并在一小部分时间内解决谜题,通常比人类更快。这个解决方案没有什么特别之处,它使用了基于硅的逻辑(加上numpy和pandas)的力量来超越人类逻辑。关于另一种方法,请 看用人工智能解决数独问题。
你可以在Kaggle数据集中的其他900万道谜题中尝试这两种方法。
- 文章中使用的所有代码都可以 在这里找到 。
- 下载我们的Sudoku Solver Python环境,并尝试一下本文中提到的一些技术。
通过ActiveState Platform,你可以在几分钟内创建你的Python环境,就像我们为这个项目建立的一样。自己尝试一下,或者了解更多关于它如何帮助Python开发者提高工作效率的信息。