本文已参与「新人创作礼」活动，一起开启掘金创作之路。

分类

看到这个问题其实我们首先要把这些算法分一下类：

• 极大似然、交叉熵是用来计算损失（loss）的
• 梯度下降、牛顿法是用来优化的，最小二乘法是选择平方差作为loss的优化方法
  深度学习训练的时候每一轮都会计算输出loss然后根据梯度下降法进行优化

公式

最小二乘法

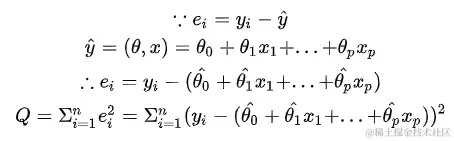
交叉熵

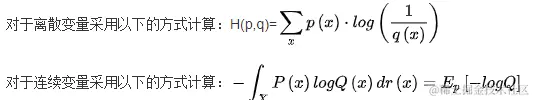
牛顿法

极大似然

区别

最小二乘法直接使用极值，将极值作为最小值。其假定有二：1，损失函数中极值就是最小值。2，损失函数具有极值。
梯度下降是用迭代的方法求出局部最优解
牛顿法需要求逆，还要求目标函数f(x)二阶可导。