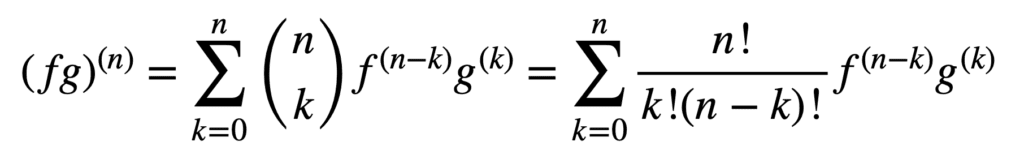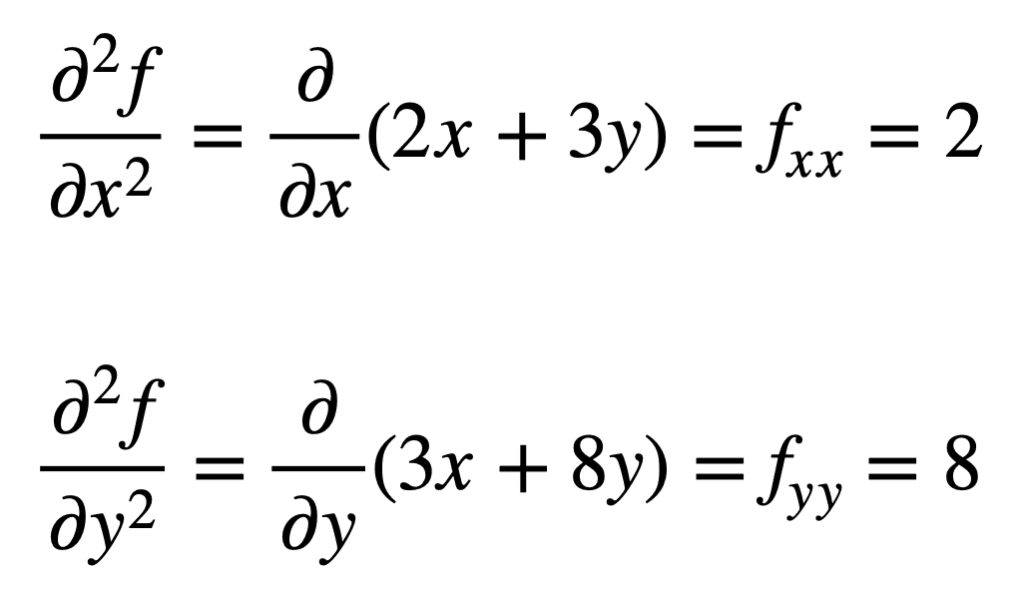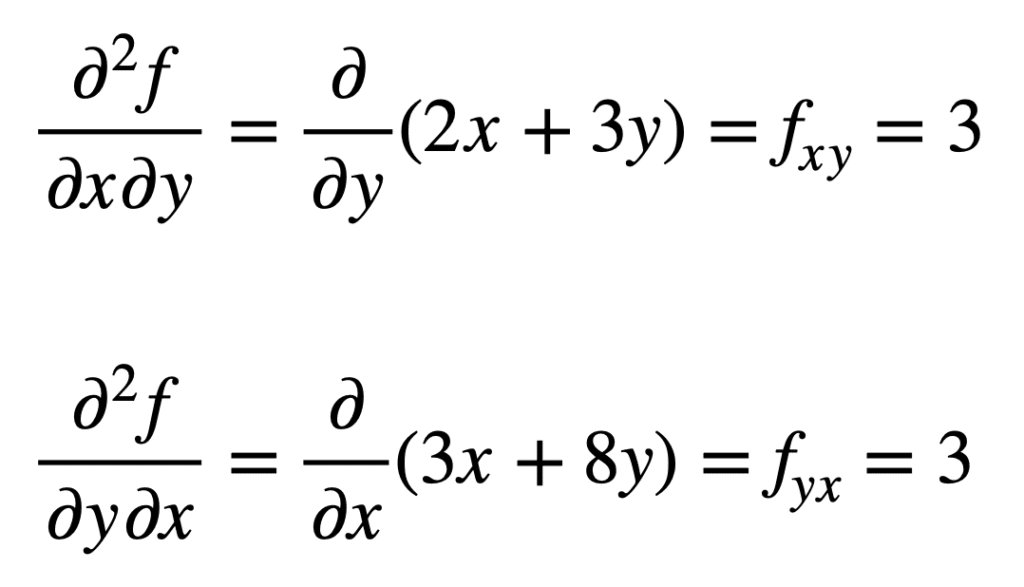鸣叫 分享 分享
最后更新于2021年7月31日
高阶导数可以捕捉到一阶导数本身无法捕捉的函数信息。
一阶导数可以捕捉重要的信息,如变化率,但就其本身而言,它们不能区分局部的最小值或最大值,在这两种情况下变化率为零。一些优化算法通过利用高阶导数来解决这一限制,例如在牛顿方法中,二阶导数被用来达到优化函数的局部最小值。
在本教程中,你将发现如何计算高阶单变量和多变量导数。
完成本教程后,你将知道。
- 如何计算单变量函数的高阶导数。
- 如何计算多变量函数的高阶导数。
- 二阶导数如何在机器学习中被二阶优化算法所利用。
让我们开始吧。
高阶导数
图片来源:Jairph,保留部分权利。
教程概述
本教程分为三个部分;它们是:。
- 单变量函数的高阶导数
- 多变量函数的高阶导数
- 机器学习中的应用
单变量函数的高阶导数
除了我们已经看到的一阶导数可以为我们提供关于一个函数的重要信息,比如它的瞬时变化率,高阶导数也同样有用。例如,二阶导数可以测量一个移动物体的加速度,或者它可以帮助优化算法区分局部最大值和局部最小值。
计算单变量函数的高阶(第二、第三或更高)导数并不难。
一个函数的二阶导数只是其一阶导数的导数。三阶导数是二阶导数的导数,四阶导数是三阶导数的导数,以此类推。
- 第147页,Calculus for Dummies,2016。
因此,计算高阶导数只需要重复微分该函数。为了做到这一点,我们可以简单地应用我们的幂律知识。让我们考虑一下函数,f_(x_)=x3+2x2-4x+1,作为一个例子。那么。
第一导数:f'(x) =3x2+4x- 4
第二导数:f''(x) =6x+ 4
第三导数:f''(x)=6
第四次导数:f (4)(x)=0
第五次导数:f (5)(x)=0_等等。_
我们在这里所做的是,我们首先对_f__(x_)应用了幂律,以获得其第一个导数_f_'(x),然后对第一个导数应用了幂律,以获得第二个导数,以此类推。随着微分法的反复应用,导数最终将归于零。
在获得高阶导数时,应用积和商规则也仍然有效,但其计算会随着阶数的增加而变得越来越混乱。一般的莱布尼兹规则简化了这方面的任务,它将乘积规则概括为。
这里,术语_n_!/k!(n- k)!,是二项式定理中的二项式系数,而f (k)和 g(k)分别表示函数_f_和_g_的第 _k_次导数。
因此,通过一般莱布尼兹规则,找到第一和第二导数(因此,分别代入_n_=1和_n_=2),就可以得到。
(fg)(1)=(fg)' =f (1) g+f g(1)
(fg)(2)=(fg)'=f (2) g+2f (1) g(1) +f g(2)
注意熟悉的第一导数是由乘积规则定义的。莱布尼兹法则也可以用来寻找有理函数的高阶导数,因为商可以有效地表达为一种形式的乘积,f g-1。
多变量函数的高阶导数
多变量函数的高阶偏导的定义与单变量的情况类似:n>1的第 n_阶偏导,被计算为(n-_1)第n阶偏导的偏导。例如,对一个有两个变量的函数进行二阶偏导,会产生四个二阶偏导:两个_自己的_偏导,f__xx_和_f__yy_和两个交叉偏导,即_f__xy_和_f__yx.
要取 "导数",我们必须取关于x或y的部分导数,有四种方法:x然后x,x然后y,y然后x,y然后y。
- 第371页,单变量和多变量微积分,2020。
让我们考虑多变量函数_f__(x_,y) =x2+3xy +4y2,我们想找到它的二次偏导数。这个过程首先要找到它的一阶偏导数。
然后通过重复寻找偏导数的过程,找到四个,二阶偏导数的偏导数。自己的_偏导数是最直接的,因为我们只是简单地重复偏微分过程,对_x_或_y,第二次。
之前找到的_f_的交叉偏导_x_(的交叉偏导(即关于_x_的偏导),通过对结果进行关于_y_的偏导来找到,得到_f__xy_.同样地,对_f_的偏导进行_y_ 的_偏导,得到_f__yx:
交叉偏导的结果是一样的,这不是偶然的。这是由Clairaut定理定义的,该定理指出,只要交叉偏导数是连续的,那么它们就是相等的。
在机器学习中的应用
在机器学习中,主要使用的是二阶导数。我们之前提到,二阶导数可以为我们提供一阶导数本身无法捕捉的信息。具体来说,它可以告诉我们一个临界点是局部最小值还是最大值(分别基于二阶导数是否大于或小于零),否则,在这两种情况下,一阶导数都是零。
有几种_二阶_优化算法可以利用这种信息,其中之一就是牛顿方法。
另一方面,二阶信息允许我们对目标函数进行二次近似,并近似正确的步长以达到局部最小值 ...
- 第87页,《优化的算法》,2019年。
在单变量情况下,牛顿方法使用二阶泰勒级数展开,围绕目标函数上的某个点进行二次逼近。牛顿方法的更新规则是通过将导数设为零并求根得到的,它涉及到对二阶导数的除法操作。如果牛顿方法被扩展到多变量优化,导数被梯度所取代,而第二导数的倒数被Hessian矩阵的逆数所取代。
我们将在单独的教程中介绍Hessian和Taylor系列近似,这两个方法利用了高阶导数的使用。
进一步阅读
如果你想深入了解,本节提供了更多关于该主题的资源。
书籍
- 单变量和多变量微积分, 2020.
- 傻瓜微积分》, 2016.
- 深度学习, 2017.
- Algorithms for Optimization, 2019.
总结
在本教程中,你发现了如何计算高阶单变量和多变量导数。
具体来说,你学到了。
- 如何计算单变量函数的高阶导数。
- 如何计算多变量函数的高阶导数。
- 二阶导数如何在机器学习中被二阶优化算法所利用。
你有什么问题吗?
在下面的评论中提出你的问题,我将尽我所能回答。
鸣叫 分享 分享
The postHigher-Order Derivativesappeared first onMachine Learning Mastery.