鸣叫 分享 分享
偏导数和梯度向量在机器学习算法中经常被用来寻找函数的最小或最大。梯度向量被用于神经网络的训练、逻辑回归以及许多其他分类和回归问题。
在本教程中,你将发现偏导数和梯度向量。
完成本教程后,你将知道。
- 几个变量的函数
- 两个变量的函数的水平集、等值线和图形
- 多个变量的函数的偏导数
- 梯度向量及其含义
让我们开始吧。
局部导数和梯度矢量的温和介绍。Atif Gulzar的照片,保留部分权利。
教程概述
本教程分为三个部分;它们是:。
- 几个变量的功能
- 水平集
- 等高线
- 图形
- 部分导数的定义
- 梯度向量
- 梯度向量代表什么
几个变量的函数
你可以在本教程中回顾一下函数的概念和几个变量的函数。 我们将在这里提供有关几个变量的函数的更多细节。
一个多变量函数具有以下特性。
- 它的域是由(x_1, x_2, x_3, ..., x_n)给出的n个元组的集合。
- 它的范围是一个实数的集合
例如,下面是一个两个变量的函数(n=2)。
f_1(x,y) = x + y
在上述函数中,x和y是自变量。它们的总和决定了该函数的值。这个函数的域是XY软平面上所有点的集合。这个函数的绘图需要在三维空间中绘制,两个轴代表输入点(x,y),第三个轴代表f的值。
下面是另一个双变量函数的例子。 f_2(x,y) = x*_x + y*_y
为了保持简单,我们将做两个变量的函数的例子。当然,在机器学习中,你会遇到数百个变量的函数。与两个变量的函数有关的概念可以扩展到这些情况。
水平集和双变量函数的图形
平面上的点的集合,其中函数f(x,y)有一个常值,即f(x,y)=c,是f的水平集或水平曲线。
举例来说,对于函数f_1,所有满足以下方程的(x,y)点都定义为f_1的水平集。
x + y = 1
我们可以看到,这个水平集有一个无限的点集,例如,(0,2),(1,1),(2,0)等。这个水平集在XY平面上定义了一条直线。
一般来说,f_1的所有水平集都定义了形式为(c是任何实际常数)的直线。
x + y = c
类似地,对于函数f_2,一个水平集的例子是。
x*_x + y*_y = 1
我们可以看到,任何位于半径为1、中心在(0,0)的圆上的点都满足上述表达。因此,这个水平集由位于这个圆上的所有点组成。同样地,f_2的任何水平集都满足以下表达式(c是任何实际常数>=0)。
x*_x+y*_y=c
因此,f_2的所有水平集都是中心在(0,0)的圆,每个水平集都有自己的半径。
函数f(x,y)的图形是所有点(x,y,f(x,y))的集合。它也被称为一个曲面z=f(x,y)。f_1和f_2的图形如下(左侧)。
函数f_1和f_2及其相应的轮廓线
双变量函数的等值线
假设我们有一个两变量的函数f(x,y)。如果我们用一个平面z=c来切割曲面z=f(x,y),那么我们得到满足f(x,y)=c的所有点的集合。轮廓曲线是满足f(x,y)=c的点的集合,在平面z=c中。这与水平集略有不同,水平曲线是在XY平面内直接定义的。然而,许多书将轮廓线和水平曲线视为相同的。
f_1和f_2的等高线都显示在上图中(右侧)。
局部导数和梯度
函数f对变量x的偏导,用∂f/∂x表示。它的表达式可以通过微分f与x的关系来确定。例如,对于函数f_1和f_2,我们有。
∂f_1/∂x=1
∂f_2/∂x = 2x
∂f_1/∂x表示f_1相对于x的变化率。对于任何函数f(x,y),∂f/∂x表示f相对于变量x的变化率。
∂f/∂y的情况也是如此。你可以在本教程中看一下偏导的正式定义。
当我们找到所有独立变量的偏导数时,我们最终得到一个矢量。这个向量被称为f的梯度向量,用∇f(x,y)表示。f_1和f_2的梯度的一般表达式为(这里i,j是平行于坐标轴的单位向量)。
∇f_1(x,y) = ∂f_1/∂xi + ∂f_1/∂yj = i+j
∇f_2(x,y) = ∂f_2/∂xi + ∂f_2/∂yj = 2xi + 2yj
从梯度的一般表达式中,我们可以评估空间中不同点的梯度。在f_1的情况下,梯度矢量是一个常数,即。
i+j
无论我们在三维空间的哪个位置,梯度向量的方向和大小都不会改变。
对于函数f_2来说,∇f_2(x,y)随着(x,y)值的变化而变化。例如,在(1,1)和(2,1)处,f_2的梯度由以下向量给出。
∇f_2(1,1) = 2i + 2j
∇f_2(2,1) = 4i + 2j
在一个点上的梯度向量说明了什么?
几个变量的函数在任何一点的梯度向量表示最大变化率的方向。
我们可以把梯度向量与切线联系起来。如果我们站在空间的一个点上,我们想出一个规则,告诉我们沿着该点的切线走。这意味着无论我们在哪里,我们都要找到该点的等高线的切线并沿着它行走。如果我们按照这个规则走,我们最终会沿着f的轮廓线走,函数的值永远不会改变,因为函数的值在f的轮廓线上是不变的。
另一方面,梯度向量是切线的法线,指向最大增长率的方向。如果我们沿着梯度的方向走,就会开始遇到下一个函数值会大于前一个的点。
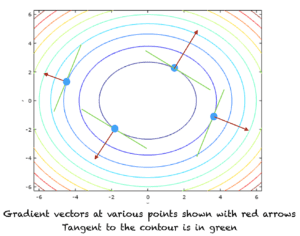
梯度的正方向表示最大增加率的方向,而负方向表示最大减少率的方向。下图显示了函数f_2轮廓线不同点的梯度向量的正方向。正的梯度方向由红色箭头表示。等高线的切线显示为绿色。
等高线和梯度向量的方向
为什么梯度向量在机器学习中很重要?
梯度向量在机器学习算法中非常重要,而且经常使用。在分类和回归问题中,我们通常定义均方误差函数。沿着这个函数的梯度的负方向,我们就能找到这个函数的最小值的点。
函数的情况也类似,将其最大化会导致实现最大的准确性。在这种情况下,我们将遵循这个函数的最大增加率的方向或梯度向量的正方向。
扩展
本节列出了一些扩展本教程的想法,你可能想探索一下。
- 梯度下降/梯度上升
- Hessian矩阵
- 雅各邦
如果你对这些扩展进行了探索,我很想知道。请在下面的评论中发表你的发现。
进一步阅读
如果你想深入了解,本节提供了更多关于该主题的资源。
教程
资源
- 关于机器学习的微积分书籍的其他资源
书籍
- 托马斯的微积分,第14版,2017年。(基于George B. Thomas的原作,由Joel Hass, Christopher Heil, Maurice Weir修订)
- 微积分》,第3版,2017年。(Gilbert Strang)
- 微积分》,第8版,2015年。(詹姆斯-斯图尔特)
摘要
在本教程中,你发现了什么是几个变量的函数、偏导数和梯度向量。具体来说,你学到了。
- 几个变量的函数
- 几个变量的函数的等值线
- 多变量函数的水平集
- 多变量函数的部分导数
- 梯度向量及其意义
你有什么问题吗?
请在下面的评论中提出你的问题,我将尽力回答。
鸣叫 分享 分享
The postA Gentle Introduction To Partial Derivatives and Gradient Vectorsappeared first onMachine Learning Mastery.