SLAM中的坐标系旋转变换以及旋转矩阵的左乘和右乘问题本文已参与「新人创作礼」活动，一起开启掘金创作之路。对于一个变换

本文已参与「新人创作礼」活动，一起开启掘金创作之路。

对于一个变换矩阵 $T$ ，具体的定义因人而异，例如一个变换 $T_{wc}$ ，代表了从相机坐标系到世界坐标系的变换，但是其基准（base）坐标系有时候定义为 $w$ ，也可以定义为 $c$ ，基准坐标系的不同，直接导致变换相反。

例如对于下图中的三个简单的坐标系，分别为相机坐标系 $c1，c2$ ，世界坐标系 $w$ ，其中点 $P$ 在坐标系 $c1$ 下。接下来定义变换矩阵，为了简化计算，其中三个坐标系没有旋转，只需要考虑平移。

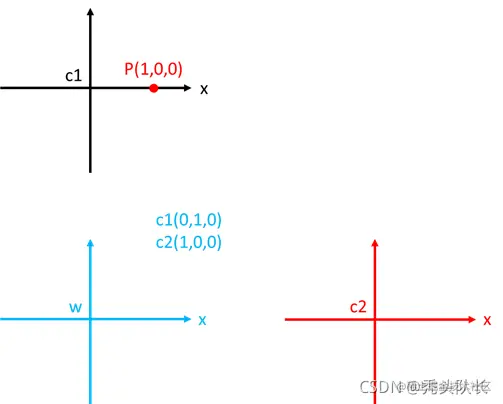
在这里插入图片描述

对于变换矩阵 $T_{cw}$ ，理解为world到camera的变换，如果以 camera 为基准坐标系，所以如果想将点 $P$ 旋转到 $c2$ 坐标系下，那么变换矩阵的定义：

T_{c_1w} = \left[ \begin{array}{ccc|c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & -1 \\ 0 & 0 & 1& 0 \\ \hline 0 & 0 & 0 & 1 \\ \end{array} \right] T_{c_2w} = \left[ \begin{array}{ccc|c} 1 & 0 & 0 & -1 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1& 0 \\ \hline 0 & 0 & 0 & 1 \\ \end{array} \right] T_{c_2c_1} = \left[ \begin{array}{ccc|c} 1 & 0 & 0 & -1 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 1& 0 \\ \hline 0 & 0 & 0 & 1 \\ \end{array} \right]

那么将一个点从 $c_1$ 坐标系转换到 $c_2$ 坐标系，需要先转换到世界坐标系。那么如下：

^{c_2}P=T_{c_2w}T_{wc_1} {^{c_1}P} = T_{c_2w} T^{-1}_{c_1w}{^{c_1}P} = \left[ \begin{array}{ccc|c} 1 & 0 & 0 & -1 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1& 0 \\ \hline 0 & 0 & 0 & 1 \\ \end{array} \right] \left[ \begin{array}{ccc|c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 1& 0 \\ \hline 0 & 0 & 0 & 1 \\ \end{array} \right] \left[ \begin{array}{cc} 1 \\ 0 \\ 0 \\ \hline 1 \\ \end{array} \right]

= \left[ \begin{array}{ccc|c} 1 & 0 & 0 & -1 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 1& 0 \\ \hline 0 & 0 & 0 & 1 \\ \end{array} \right] \left[ \begin{array}{cc} 1 \\ 0 \\ 0 \\ \hline 1 \\ \end{array} \right] =\left[ \begin{array}{cc} 0 \\ 1 \\ 0 \\ \hline 1 \\ \end{array} \right]

那么对于变换矩阵 $T_{cw}$ ，理解为world到camera的变换，如果以 world 为基准坐标系，所以如果想将点 $P$ 旋转到 $c2$ 坐标系下，那么变换矩阵的定义：

T_{c_1w} = \left[ \begin{array}{ccc|c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 1& 0 \\ \hline 0 & 0 & 0 & 1 \\ \end{array} \right] T_{c_2w} = \left[ \begin{array}{ccc|c} 1 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1& 0 \\ \hline 0 & 0 & 0 & 1 \\ \end{array} \right] T_{c_2c_1} = \left[ \begin{array}{ccc|c} 1 & 0 & 0 & 1 \\ 0 & 1 & 0 & -1 \\ 0 & 0 & 1& 0 \\ \hline 0 & 0 & 0 & 1 \\ \end{array} \right]

对于点P，假设其姿态与c1坐标系一致，则

T_{pc_1} = \left[ \begin{array}{ccc|c} 1 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1& 0 \\ \hline 0 & 0 & 0 & 1 \\ \end{array} \right]

那么可以得到，从c2到P的变换，等于从c2到c1的变换乘c1到P的变换：

T_{pc_2} = T_{c_1c_2}T_{pc_1} = \left[ \begin{array}{ccc|c} 1 & 0 & 0 & -1 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 1& 0 \\ \hline 0 & 0 & 0 & 1 \\ \end{array} \right] \left[ \begin{array}{ccc|c} 1 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1& 0 \\ \hline 0 & 0 & 0 & 1 \\ \end{array} \right] = \left[ \begin{array}{ccc|c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 1& 0 \\ \hline 0 & 0 & 0 & 1 \\ \end{array} \right]

所以在c2坐标系下，P点的坐标为 $( 0 , 1 ,0)$

对于上面两种定义方式，都可以求得正确的结果，但是定义不同，计算方式就不同。