从0.1+0.2!=0.3开始探讨进制转换

前言

我们都知道0.1+0.2!=0.3是因为计算机使用二进制存储小数时发生了精度丢失，那究竟是怎么丢的呢？最近我想仔细梳理一下这个问题，结果一梳理发现自己对进制转换好像从来不了解，赶紧恶补，终有此文。

0.1+0.2!=0.3的原理分析

IEEE754标准

IEEE754是计算机通用的一套二进制浮点数算术标准，定义了浮点数在计算机中的存储格式，格式包括：S、E、M三个部分，他们按照如下公式表示浮点数：

$(-1)^S*1.M*2^{E-127}$

S：Sign，阶符，符号位，0表示正数，1表示负数

E: Exponent，阶码，指数偏移值

M：Fraction，尾数，有效数字

不同精度浮点数各部分位数如下：

精度	总位数	S	E	M
Float	32	1	8	23
Double	64	1	11	52

其实从这里我们就能看出来，即便是双精度浮点数的有效数字也只有52位，对于很多无限循环小数只能进行截断处理，这就是精度丢失的原因。

10进制浮点数转2进制

我们挑一个简单的，将10.125转成IEEE754单精度格式。

1. 分别将整数和小数转成二进制

整数使用除基取余倒排法,小数使用乘基取整正排法，转换方法后面有，这里就不写了。

$10_D = 1010_B$

$0.125_D = 0.001_B$

将两者组合得到二进制浮点数$1010.001_B$。

2. 按照公式确认S、E、M

根据我们得到的二进制浮点数$1010.001_B$：

首先，浮点数为正，所以$S=0_B$。

其次，将浮点数用科学计数法表述，得到$1.010001*2^3_B$,

于是我们得到：$M=0100010000..._B$，$E-127 = 3$，进而$E=130_D$

将$E=130_D$转成二进制得到$E=10000010_B$

3. 将S、E、M组合得到最终结果

$10.125_D = 0100000100100010000..._B$

转成16进制，$10.125_D = 41220000_H$

2进制浮点数转10进制

我们把刚才$41220000_H$给转回来。

1. 拆分出S、E、M

根据SEM的结果 $41220000_H = 0100000100100010000..._B$，我们得到：$S=0_B$，$E=10000010_B$，$M=0100010000..._B$

将E转成十进制，得到$E=10000010_B=130_D$

2. 按照公式还原浮点数

$(-1)^S*1.M*2^{E-127} = 1*1.010001_B*2^3 = 1010.001$

3. 分别将二进制整数和小数转成十进制

这里使用按权相加法进行转换，方法会在后面介绍。

$1010_B=10_D$

$0.001_B=0.125_D$

最终我们得到十进制浮点数：$10.125_D$

分析一下0.1+0.2!=0.3

首先，0.1和0.2转成二进制浮点数为：

$0.1_D=0.0001100110011..._B$

$0.2_D=0.001100110011..._B$

我们发现，这两个二进制浮点数都是无限循环小数，而在IEEE754标准中，尾数M的位数都是有限的，计算机只能对多余的部分进行截取，这就意味着0.1和0.2在计算机中都丢失了精度，于是相加就不等于0.3了。

好了，到这里算是复习，后面才是我想讨论的。

进制转换原理分析

上面我们用到了很多进制转换的方法，那这些方法的原理究竟是什么，我之前从来没有想过，下面来探讨一下。

进制转换基本方法

1. 如果高进制转低进制：

   a. 对于整数，使用除基取余倒排法
   b. 对于小数，使用乘基取整正排法

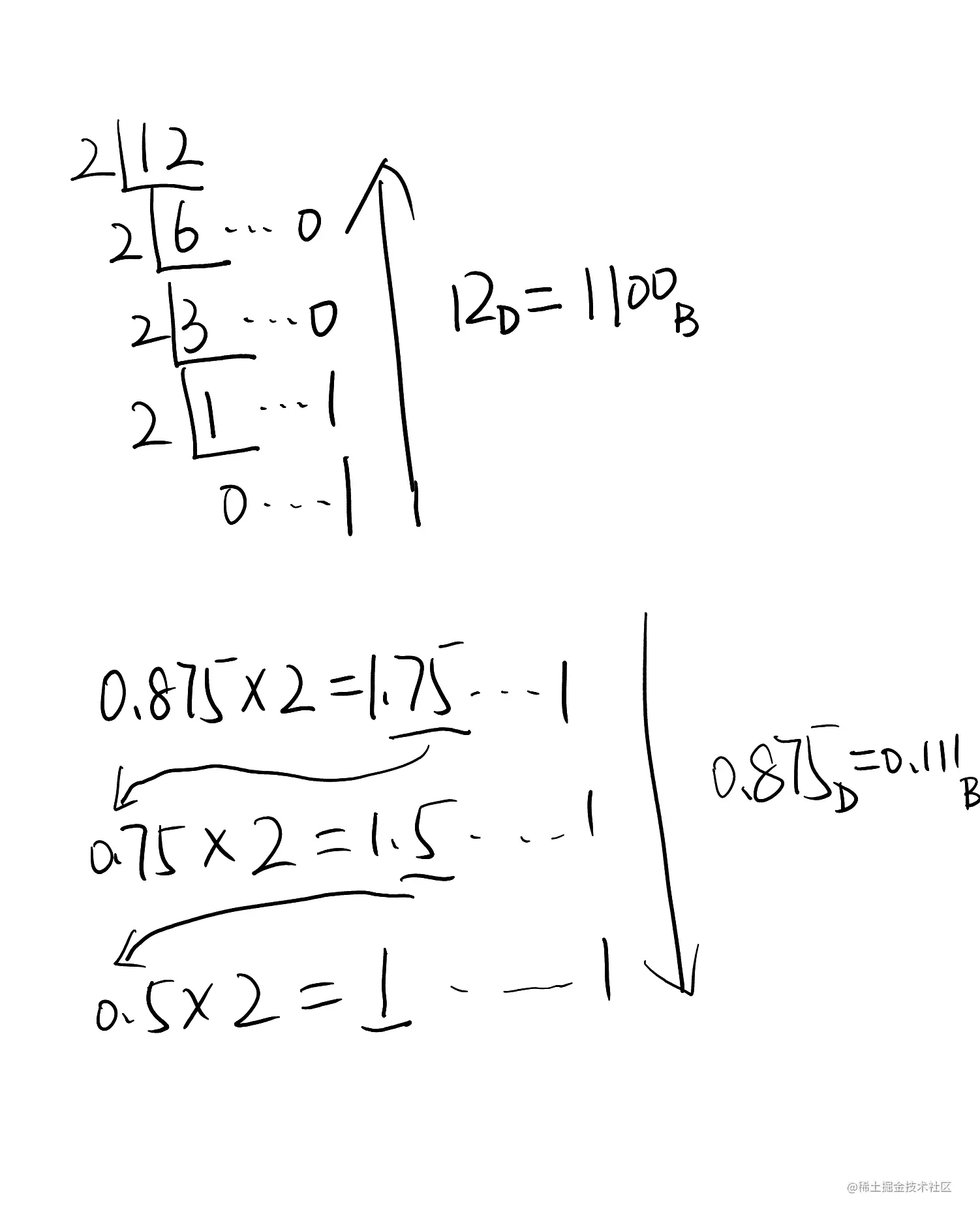
2. 如果低进制转高进制：

   不论整数还是小数，使用按权相加法

   $1100_B = 1*2^3+1*2^2+0*2^1+0*2^0=12_D$

   $0.111_B = 1*2^{-1}+1*2^{-2}+1*2^{-3} = 0.875_D$

进制转换的原理

除基取余倒排法原理

首先，任意一个整数都可以分解为以基数为底的幂组成的多项式。

$Z_H = a_nH^n + a_{n-1}H^{n-1}+...+a_1H^1+a_0H^0$

$Z_D = a_nD^n + a_{n-1}D^{n-1}+...+a_1D^1+a_0D^0$

$Z_O = a_nO^n + a_{n-1}O^{n-1}+...+a_1O^1+a_0O^0$

$Z_B = a_nB^n + a_{n-1}B^{n-1}+...+a_1B^1+a_0B^0$

H、D、O、B分别表示16进制、10进制、8进制、2进制 所谓的基数就是常说的进制，不管是什么进制都可以拆分为多项式。这很好理解，因为这就是整数组合的方式，比如$100_D = 1*10^2+0*10^1+0*10^0$。

以十进制整数转换二进制举例，二进制的多项式可以进一步转化为：

$Z_B = a_nB^n + a_{n-1}B^{n-1}+...+a_1B^1+a_0B^0 \\ \quad\,\,\,= a_nB^n + a_{n-1}B^{n-1}+...+a_1B^1+a_0\\ \quad\,\,\,= B(a_nB^{n-1}+a_{n-1}B^{n-2}+...+a_1)+a_0\\ \quad\,\,\,= B(B(a_nB^{n-1}+a_{n-1}B^{n-2}+...+a_2)+a_1)+a_0\\ \quad\,\,\,...$

我们只需要把提取出来的$B$给除掉，就可以得到余数部分，这就是除基取余倒排法的原理。

乘基取整正排法原理

接下来看小数，小数同样也可以分解为多项式。

$Z_H = a_nH^{-1} + a_{n-1}H^{-2}+...+a_1H^{-n}$

$Z_D = a_nD^{-1} + a_{n-1}D^{-2}+...+a_1D^{-n}$

$Z_O = a_nO^{-1} + a_{n-1}O^{-2}+...+a_1O^{-n}$

$Z_B = a_nB^{-1} + a_{n-1}B^{-2}+...+a_1B^{-n}$

以十进制小数转换二进制举例，二进制的多项式可以进一步转化为：

$Z_B = a_nB^{-1} + a_{n-1}B^{-2}+...+a_1B^{-n} \\ \quad\,\,\,= B^{-1}(a_n+a_{n-1}B^{-1}+...+a_1B^{-n+1})\\ \quad\,\,\,= B^{-1}(a_n+B^{-1}(a_{n-1}+...+a_1B^{-n+2})\\ \quad\,\,\,...$

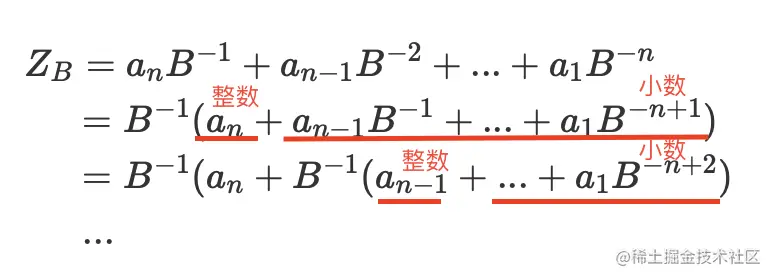
我们只需要把提取出来的$B^{-1}$给乘掉，就可以得到整数部分，这就是乘基取整正排法的原理。

按权相加法原理

按权相加法其实就是上面的多项式所体现出来的过程，只不过在计算时要按照目标进制的规则进行计算。如果是二进制转十进制，那么在多项式按权相加的过程中，就要逢十进一，如果是二进制转十六进制，那么在过程中就要逢十六进一。

可能的几个疑惑

为什么加权相加的结果是十进制？

这是因为我们是在用十进制的规则对结果进行计算，只是因为我们对十进制太熟悉的，而不察觉。比如下面这个例子：

$101010_B = 1*2^5+0*2^4+1*2^3+0*2^2+1*2^1+0*2^0\\ \quad\quad\quad\,\,\,\,\,= 32+0+8+0+2+0 \\ \quad\quad\quad\,\,\,\,\,= 42_D\\ \quad\quad\quad\,\,\,\,\,= 2A_H\\ \quad\quad\quad\,\,\,\,\,= 52_H$

计算过程中如果逢10进1就得到42，如果逢16进1就得到2A，如果逢8进一就得到52。进制只是数字的表达方式，数字大小本身没有改变。

低进制转高进制可以用除基取余法吗？

可以，不过比较麻烦。

其实上面的进制转换方法可以分为两类：

第一类是基于多项式，通过消掉基数的方法获取系数，不论是除基取余还是乘基取整。

第二类是基于多项式，直接相加，通过计算过程中进位的方式获取系数，按权相加法就是这种。

这两种方法都是可以达成目的的，只是各自适合特定的场景。

对于除基取余法，小进制的基始终处于大进制基的范围以内，比如2就在0-9范围内，这样在除的时候就可以方便的进行按位比较，而反过来，大进制的基超过小进制的基，那在除的时候就得多位比较，不容易计算。

我试了一下用除基取余法将二进制转换成十进制，如下：

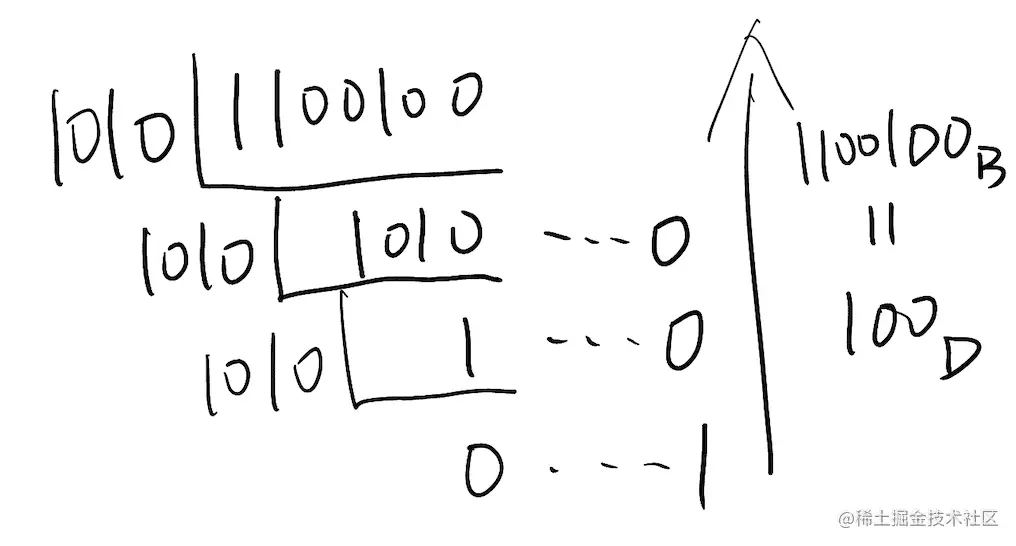
对于按权相加法，小进制的数可以累加达到大进制的基数，很方便实现进位，但大进制的数只能通过拆解才能达到小进制的基数，还怎么相加呢？

尾声

这篇文章写了一天，真的是很折磨，不过技术这个东西，偶尔就得较较真，总是能发现很多新东西。