什么是RSA算法
公开密钥密码学(英语:Public-key cryptography)也称非对称式密码学(英语:Asymmetric cryptography)是密码学的一种算法,它需要两个密钥,一个是公开密钥,另一个是私有密钥;公钥用作加密,私钥则用作解密。而RSA是一种非对称加密算法,它的名字是由它的三位开发者,即 Ron Rivest、Adi Shamir 和 Leonard Adleman 的姓氏的首字母组成的 (Rivest-Shamir-Adleman)。RSA 可以被用于公钥密码和数字签名。对极大整数做因数分解的难度决定了 RSA 算法的可靠性,只要其钥匙的长度足够长,用RSA加密的信息实际上是不能被破解的。

RSA算法的数学基础
互质关系(coprime)
如果两个正整数,除了1以外,没有其他的公因子,则称这两个数为互质关系。比如,15和32没有公因子,所以它们是互质关系。这说明,不是质数也可以构成互质关系。
欧拉函数
RSA算法的核心数学原理,欧拉函数的目的是任意给定正整数n,在小于等于n的正整数之中,求解出有多少个与n构成互质关系?
以φ(n)表示。在1到8之中,与8形成互质关系的是1、3、5、7,所以 φ(n) = 4。其数学表达式为:
欧拉函数是积性函数,即是说若m,n互质,则
模反元素
如果两个正整数a和n互质,那么一定可以找到整数b,使得 ab-1 被n整除,或者说ab被n除的余数是1,如下 ,则这时,b就叫做a的"模反元素"。
RSA算法的应用
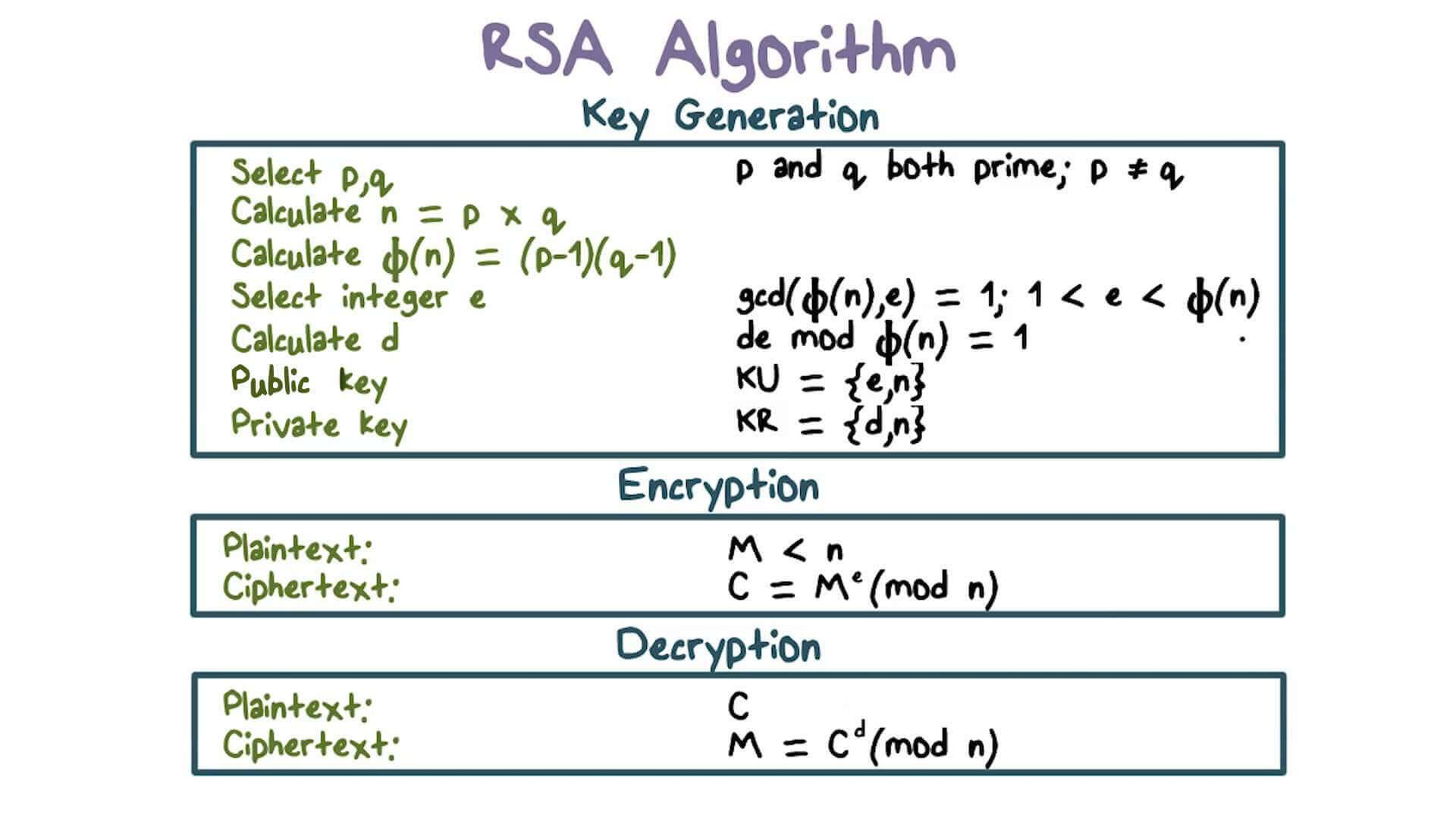
生成密钥
- 随机选择两个不相等的质数p和q(尽量选择大的,难破解)
- 计算p和q的乘积n
- 计算n的欧拉函数,即
- 随机选择一个整数e,满足,且e和互质,一般选择65537
- 计算e相对于的模反元素d
- 将n和e封装成公钥,n和d封装为私钥
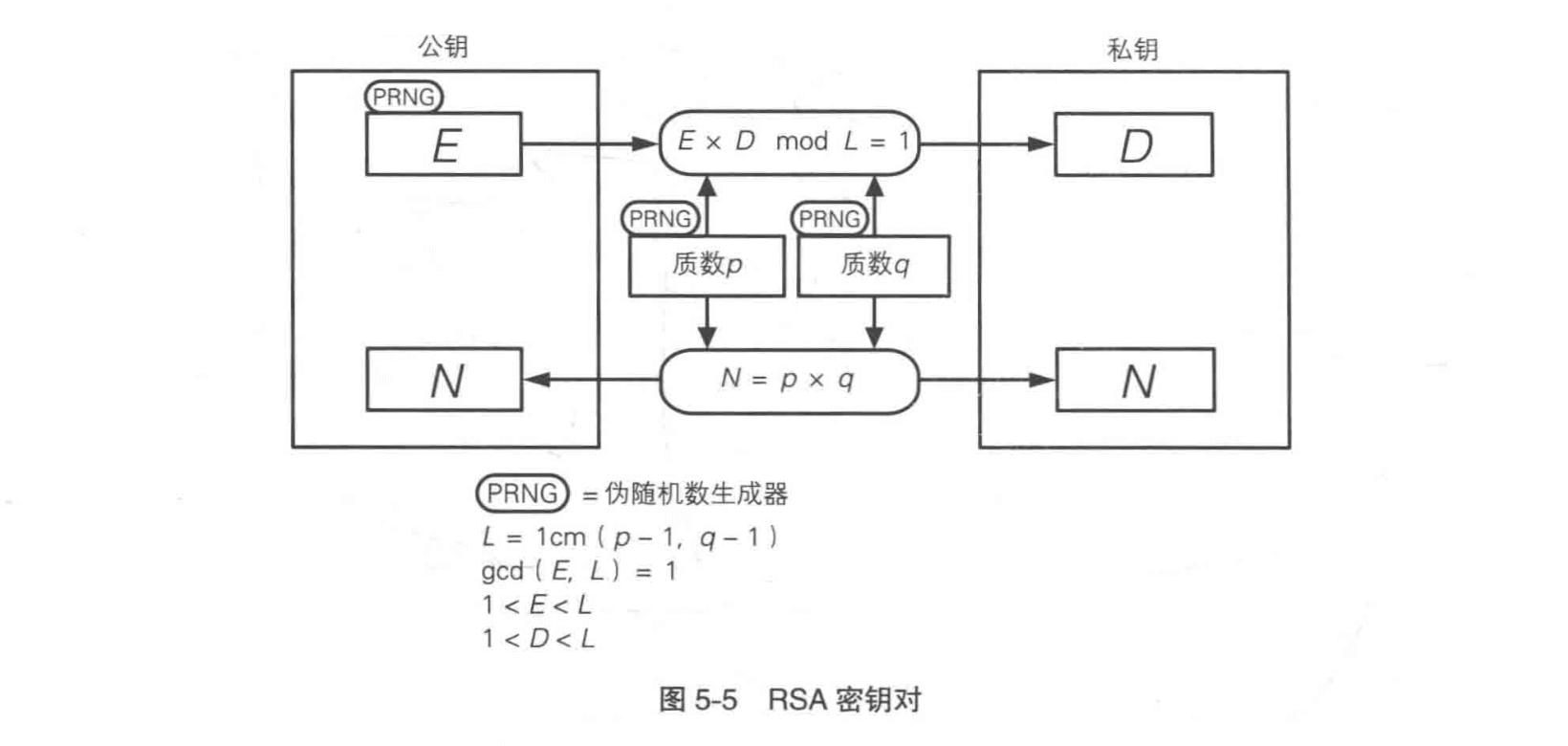
在实际应用中,n和e黑客是可以获取到的,但是要对信息进行解密,就必须知道d,而d的生成时根据e和p和q来生成的,而p和q的获取,要对n进行因式分解,在当前的计算机体系下,大整数的因数分解,是一件非常困难的事情。如果n的位数为2048位,基于现阶段的计算机技术(2022年),极难破解。
消息加密
加密要用公钥 (n,e),假设鲍勃要向爱丽丝发送加密信息m,他就要用爱丽丝的公钥 (n,e) 对m进行加密。这里需要注意,m必须是整数(字符串可以取ascii值或unicode值),且m必须小于n。
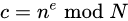
消息解密
爱丽丝得到鲍伯的消息c后就可以利用她的密钥d来解码。她可以用以下这个公式来将c转换为n.
解码原理:
RSA算法的相关攻击
大数因式分解
2009年12月12日,编号为RSA-768(768 bits, 232 digits)数也被成功分解[10]。这一事件威胁了现通行的1024-bit密钥的安全性,普遍认为用户应尽快升级到2048-bit或以上。
中间人攻击
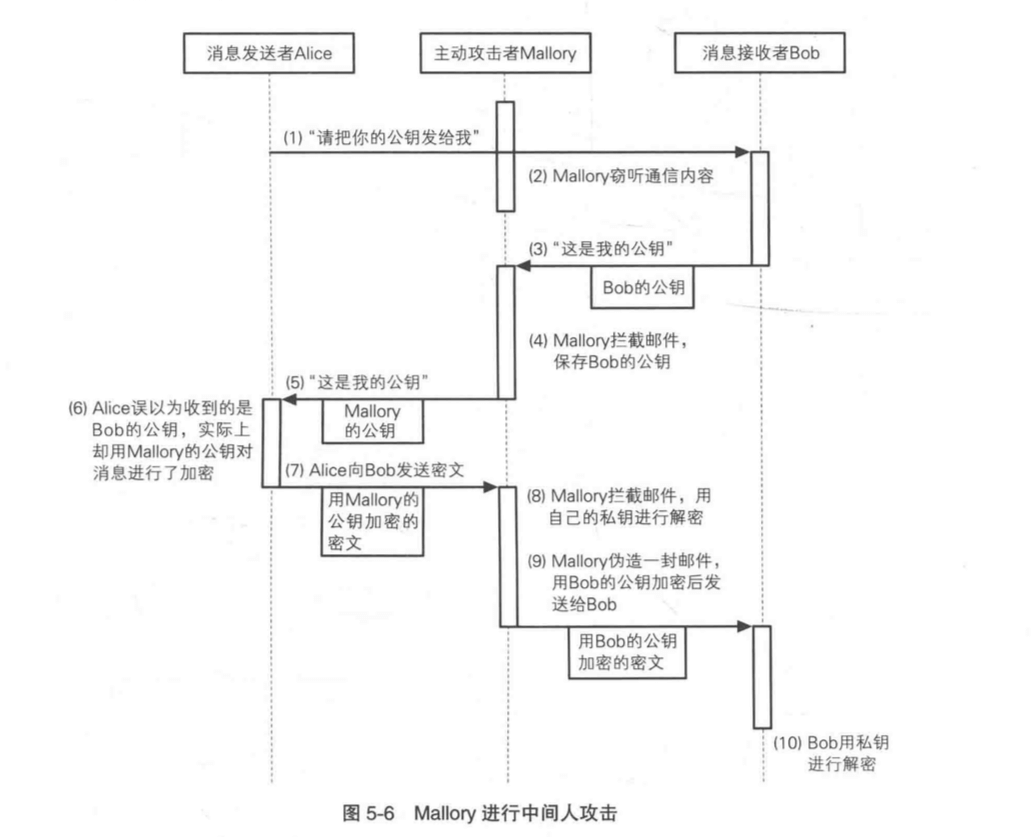
主动攻击者 Mallory 在通信双方之间拦截各自的公钥。并且分别向两者发送自己的公钥。这样攻击者就可以在中间截获两边的密文,并且用自己的私钥进行解密。解密得到明文以后就可以任意篡改原文。最终达到攻击的目的。
这种攻击仅仅靠 RSA 本身是无法防御的。要想防御中间人攻击需要用到认证相关的算法。
RSA的缺点
- 产生密钥很麻烦,受到素数产生技术的限制,因而难以做到一次一密,在混合加密过程中,没办法像DH那样生成会话密钥,容易导致前向安全问题
- 分组长度太大,为保证安全性,n 至少也要 600 bits 以上,使运算代价很高,尤其是速度较慢