剑指 Offer 30. 包含min函数的栈
一起养成写作习惯!这是我参与「掘金日新计划 · 4 月更文挑战」的第13天,点击查看活动详情。
思路
(单调栈) O(1)
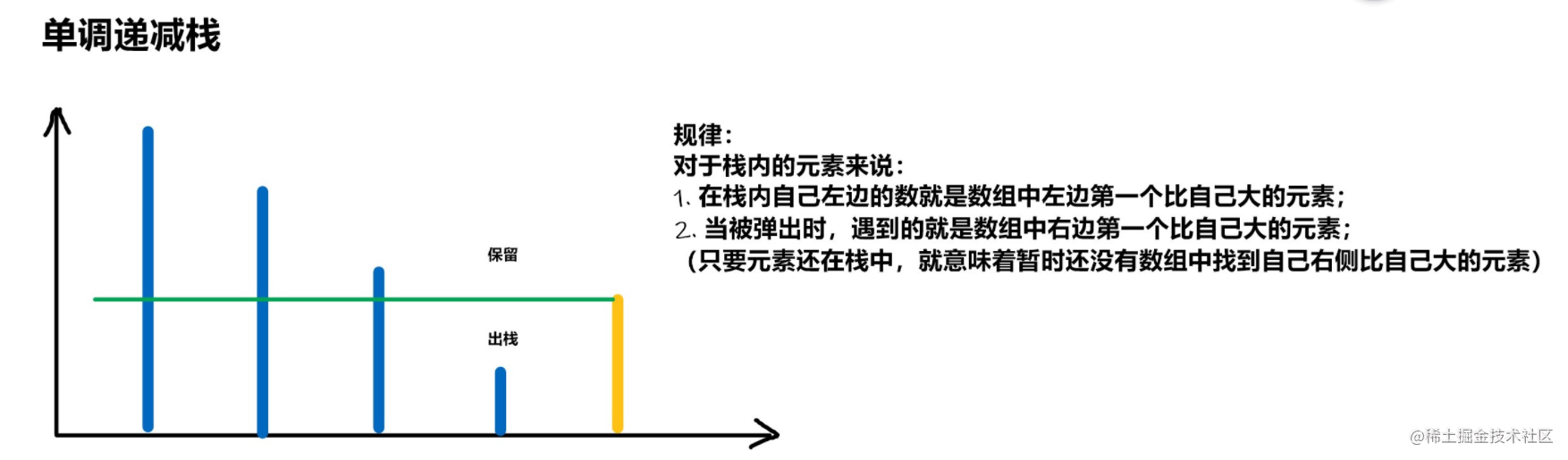
我们除了维护基本的栈stackValue结构之外,还需要维护一个单调递减栈stackMin,来实现返回最小值的操作。
push操作
- 1、直接向普通栈
stackValue压入。 - 2、如果该数
≤单调栈stackMin的栈顶元素,则将该数同时压入单调栈中;否则,不压入。
pop()操作
- 1、如果普通栈顶元素
==单调栈stackMin的栈顶元素,则弹出单调栈顶元素;否则,不弹出。 - 2、直接弹出普通栈顶元素
时间复杂度分析: 四种操作都只有常数次入栈出栈操作,所以时间复杂度都是 O(1)。
c++代码
class MinStack {
public:
stack<int> stackValue;
stack<int> stackMin;
MinStack() {
}
void push(int x) {
stackValue.push(x);
if(stackMin.empty() || stackMin.top() >= x) stackMin.push(x);
}
void pop() {
if(stackValue.top() == stackMin.top()) stackMin.pop();
stackValue.pop();
}
int top() {
return stackValue.top();
}
int min() {
return stackMin.top();
}
};
剑指 Offer 31. 栈的压入、弹出序列*
思路
(栈,模拟) O(n)
1、我们定义一个空栈st,然后模拟这个过程。
2、遍历popped数组,假设我们已经处理了出栈序列中的前i - 1个数,对于当前要出栈的元素popped[i]:
- 如果栈首元素和
popped[i]不相等,我们就从pushed数组中,不断将数组元素压入st栈中,直到popped[i]入栈。 - 如果栈首元素和
popped[i]相等,则将栈首出栈,否则的话,该序列不合法,我们返回false。
3、最后判断st是否为空,为空则表示弹出序列合法,否则不合法。
时间复杂度分析: 遍历整个出栈序列的时间复杂度为O(n),while循环最多执行n次,因此总的时间复杂度为O(n)。
c++代码
class Solution {
public:
bool validateStackSequences(vector<int>& pushed, vector<int>& popped) {
stack<int> st;
int k = 0;
for(int i = 0; i < popped.size(); i++){
while(st.empty() || (st.top() != popped[i] && k != pushed.size())) st.push(pushed[k++]);
if(st.top() == popped[i]) st.pop();
else return false;
}
return st.empty();
}
};
剑指 Offer 32 - I. 从上到下打印二叉树
思路
(BFS) O(n)
我们从根节点开始按宽度优先的顺序遍历整棵树,每次先扩展左儿子,再扩展右儿子。
这样我们会:
- 先扩展根节点;
- 再依次扩展根节点的左右儿子,也就是从左到右扩展第二层节点;
- 再依次从左到右扩展第三层节点;
- 依次类推
所以BFS的顺序就是这道题目要求的顺序。
时间复杂度分析: 每个节点仅被遍历一次,所以时间复杂度是 O(n)。
c++代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
// 广度优先遍历
vector<int> levelOrder(TreeNode* root) {
vector<int> res;
if(!root) return res;
queue<TreeNode*> q;
q.push(root);
while(q.size()){
TreeNode * t = q.front();
q.pop();
res.push_back(t->val);
if(t->left) q.push(t->left);
if(t->right)q.push(t->right);
}
return res;
}
};