本文已参与「新人创作礼」活动,一起开启掘金创作之路。
时态逻辑分为线性时态逻辑和分叉时态逻辑,分叉时态逻辑里面有一种逻辑叫做计算树逻辑
线性时态逻辑(Linear temporal logic,简称LTL)
线性时间属性(LT property)
- 一个线性时间属性是在AP上的一组无限路径,我们通常很难直接指出这些属性是什么,但我们可以使用逻辑简洁地指定这些属性的规律,先让我们来看一下直接指出互斥现象和饥饿自由在每个时刻的方法:
- 在AP={c1,c2}上指定互斥现象的方法:
- Pmutex=A0A1A2⋯(无限字),且对于0≤i有{c1,c2}⊈Ai
- 在AP={c1,w1,c2,w2}上指定饥饿自由的方法:
- Pnostarve=A0A1A2⋯(无限字),且
(∃∞j.w1∈Aj)⇒(∃∞j.c1∈Aj)∧(∃∞j.w2∈Aj)⇒(∃∞j.c2∈Aj)
- 互斥现象:两个进程不可以同时进入临界资源
- 饥饿自由:当我不停的等待进入临界资源的时候,我最终可以不停的进入临界资源
- LTL的作用:描述LT特性的逻辑,但又不给出具体的时刻,只有时间的相对特性
LTL的语法
-
命题逻辑:描述系统在某一时刻的静态行为,LTL中最常用的是以下三种:
- 原子命题:a∈AP
- 否定律:¬ϕ
- 结合律:ϕ∧ψ
-
时态算子:描述系统在轨迹下所具有的性质,最基本的有以下两种:
- 下一时刻满足ϕ:◯ϕ,读作next
- 每一时刻一直满足ϕ直到ψ:ϕ⋃ψ,读作until
-
由命题逻辑和时态算子派生出的算子:
- ϕ∨ψ≡¬(¬ϕ∧¬ψ)
- ϕ⇒ψ≡¬ϕ∨ψ
- ϕ⇔ψ≡(ϕ⇒ψ)∧(ψ⇒ϕ)
- ϕ⨁ψ≡(ϕ∧¬ψ)∧(¬ϕ∧ψ)
- true≡ϕ∨ψ
- false≡¬true
- ◊ϕ≡true Uϕ
◊读作eventually,表示在未来某刻会满足ϕ
- □ϕ≡¬◊¬ϕ
□读作always,表示在此时起开始会一直满足ϕ
-
这些算子是有优先级的,¬,◯优先执行,其次是⋃,然后是∨,∧,最后是→
-
对算子的直观解释:
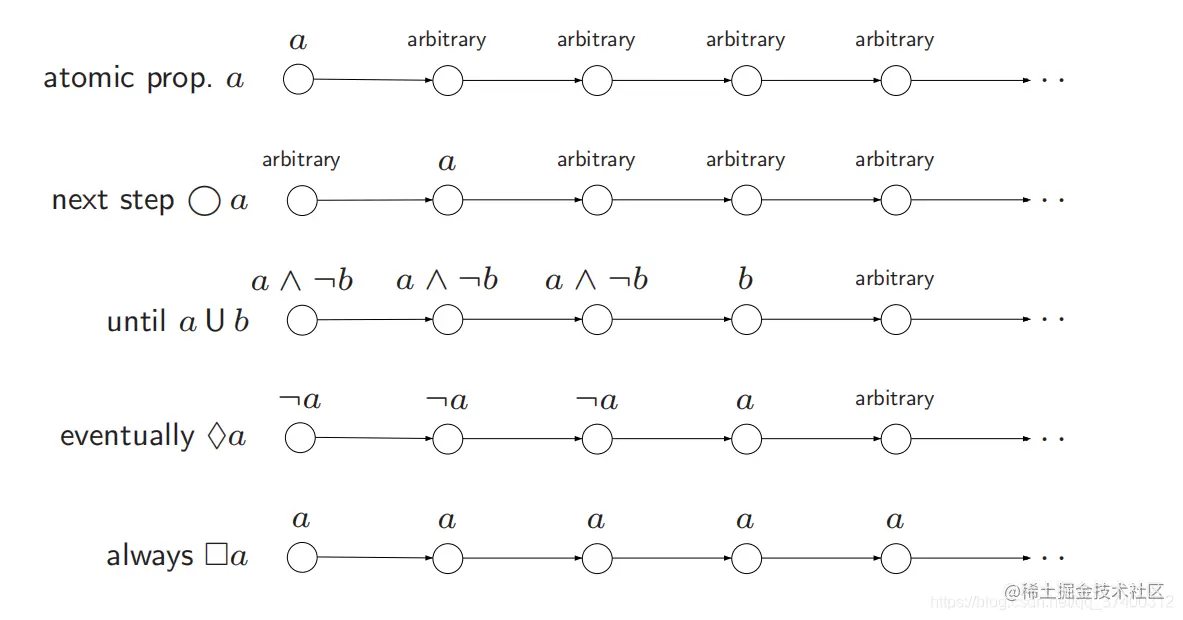
在一条轨迹上,如果从某时刻起,每个时刻只满足b,即便没出现过a,那么该时刻也满足a⋃b
-
此时,让我们用LTL语言表达互斥现象和饥饿自由在每个时刻的逻辑:
- 互斥现象:□¬(c1∧c2)
- 饥饿自由:(□◊w1⇒□◊c1)∧(□◊w2⇒□◊c2)
□◊w1理解方法:先看最外层,把◊w1看作一个ϕ,则□ϕ表示在此时起开始会一直满足ϕ;再看内层◊w1,表示无限经常次满足w1;因此,加起来表示,在此时起开始会一直无限经常次满足w1
LTL的语义
- 由LTL公式φ在AP上引起的LT性质为:Words(φ)={σ∈(2AP)ω∣σ⊨φ},其中σ是一个轨迹,σ=A0A1A2⋯,由这个LT性质可以推出如下性质:
- σ⊨true,表示路径σ一定有一条正确的路径
- σ⊨a,iff a∈A0(i.e.,A0⊨a),表示当且仅当a是状态集合A0当中的一种可能时,路径σ中包含a
A0包含了初始状态所有的可能,a只是其中的一种
- σ⊨φ1∧φ,iff σ⊨φ1 and σ⊨φ2,表示如果路径σ中包含了状态φ1和φ2,那么σ包含φ1∧φ2
i.e.表示“也就是”
- σ⊨¬φ,iff σ⊭φ
- σ⊨◯φ,iff σ[i..]=A1A2A3⋯⊨φ
σ[i..]=AiAi+1Ai+2⋯,表示从索引i开始后的σ的后缀
- σ⊨◊φ,iff ∃j⩾0.σ[j..]⊨φ
- σ⊨□φ,iff ∀j⩾0.σ[j..]⊨φ
- σ⊨□◊φ,iff ∀j⩾0.∃⩾σ[i..]⊨φ
- σ⊨◊□φ,iff ∃j⩾0.∀⩾σ[i..]⊨φ
- 范例:
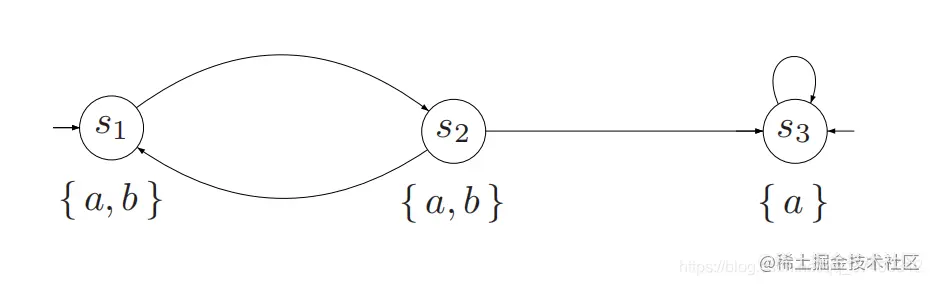 根据上图,我们可以推出这个TS的四个性质:
根据上图,我们可以推出这个TS的四个性质:
- 从初始状态开始,每一个状态都满足a,即TS⊨□a
- 从初始状态开始,每一个状态都满足,如果该状态不满足b,则该状态满足a∧¬b,即TS⊨□(¬b⇒□(a∧¬b))
- 从左边的初始状态s1开始,下一个状态可以同时满足a和b,但从右边的初始状态开始,s3的下个状态还是s3,s3并不能同时满足a和b,因此TS⊭◯(a∧b)
- 从左边的初始状态s1开始,每一个状态都满足b,直到满足a∧¬b时,不再满足b,但从右边的初始状态开始,并不满足,因此TS⊭b⋃(a∧¬b)
用LTL表示我们常见的性质
- 可达性(Reachability)
- 简单的可达性(simple reachability):◊ψ
- 多条件的可达性(conditional reachability):ϕ⋃ψ
TS系统可以既不满足◊a也不满足¬◊a:
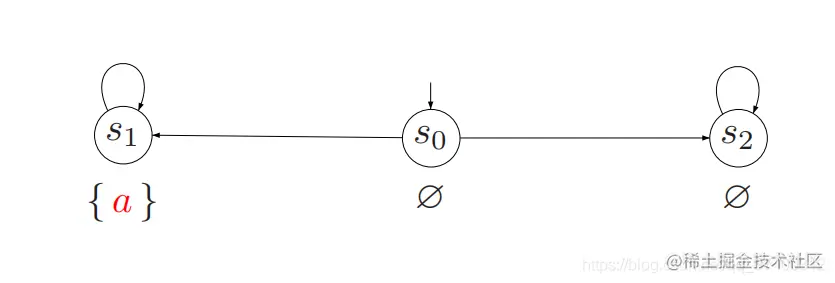
- 安全性(Safety):
- 不变性(invariant):□ϕ
- 活性(Liveness):□(ϕ⇒◊ψ)and others
- 公平性(Fairness):□◊ϕ and others
- 等价性(Equivalence):如果Words(ϕ)=Words(ψ),那么ϕ和ψ等价,表示为ϕ≡ψ
- 对偶性定律(Duality law):
- ¬□ϕ≡◊¬ϕ
- ¬◊ϕ≡□¬ϕ
- ¬◯ϕ≡◯¬ϕ
- 对偶性定律(Idempotency law):
- □□ϕ≡□ϕ
- ◊◊ϕ≡◊ϕ
- ϕ⋃(ϕ⋃ψ)≡ϕ⋃ψ
- (ϕ⋃ψ)⋃ψ≡ϕ⋃ψ
- 吸收律(Absorption law):
- ◊□◊ϕ≡□◊ϕ
- □◊□ϕ≡◊□ϕ
- 分布律(Distribution law):
- ◯(ϕ⋃ψ)≡(◯ϕ)⋃(◯ψ)
- ◊(ϕ∨ψ)≡◊ϕ∨◊ψ
- □(ϕ∧ψ)≡□ϕ∧□ψ
注意:
- ◊(ϕ⋃ψ)≡(◊ϕ)⋃(◊ψ)
- ◊(ϕ∧ψ)≡◊ϕ∧◊ψ
- □(ϕ∨ψ)≡□ϕ∨□ψ
- 下面的这个例子说明了◊(a∧b)≡◊a∧◊b:
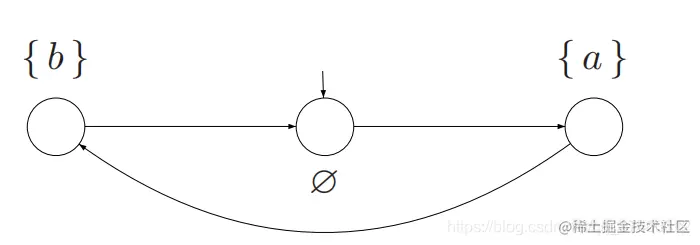 TS⊭◊(a∧b),但TS⊨◊a∧◊b)
TS⊭◊(a∧b),但TS⊨◊a∧◊b)
- 扩展律(Expansion laws):
- ϕ⋃ψ≡ψ∨(ϕ∧◯(ϕ⋃ψ))
- ◊ϕ≡ϕ∨◯◊ϕ))
- □ϕ≡ϕ∧◯□ϕ))
在这篇文章里有对这几个特性的详尽介绍:blog.csdn.net/qq_37400312…
公平性(Fairness)
- 定义:一条路径执行过程中所有过程均符合实际情况,则表示这个路径具有了公平性。
- 对于不满足公平性的路径,可以将不合实际的情况过程剔除,路径便具有了公平性。
- 无饥饿性通常是在公平性的条件下产生的。
- 公平性通常是建立活性问题的必要手段。
- 生活实例:
- 对于十字路口的两个红绿灯进程进程交错执行:TS=TrLight1∣∣TrLight2,给定一个活性性质的自然语言描述为:每个红绿灯都无限经常次处于绿灯的状态。这条性质表示红绿灯在无限次状态转化的过程中,会有无限次处于绿灯的状态。
- 轨迹:{red1,red2},{green1,red2},{red1,green2},{green1,red2}⋯,像这样的轨迹,满足刚才我们所说的活性,那么这条轨迹也具有安全性。
- 轨迹:{red1,red2},{green1,red2},{red1,red2},{green1,red2}⋯,像这样的轨迹,第二个红绿灯永远为红色,不满足刚才我们所说的活性,那么这条轨迹不具有安全性。
公平性约束(Fairness constraints)
-
解释:一个程序,有一些路径永远不会执行,那么,不管这些路径执行后是正确还是错误,我们都不需要去验证它,所以我们在验证的过程中,需要加上一些约束,来避免我们去验证一些永远不会走的路径,这个约束,我们称之为公平性约束
-
基于动作的公平性用A-fair表示,有三种情况:无条件公平性、强公平性、弱公平性
-
对于一个没有初始状态的TS=(S,Act,→,I,AP,L)
- 无初始状态
- A⊆Act
- 无限执行片段ρ=s0→α0s1→α1s2⋯
-
无条件公平性约束(Unconditional A-fair):若轨迹满足无条件公平性约束,则A中存在的一个或多个动作可以无限经常次执行。
- 解释:当ρ是一个无条件公平性路径时,对于A中的动作在这条路径上无限经常此执行,比如A={ω}⊆Act{NC,W,C},ρ=s0→NCs1→Ws2→Cs3→NC⋯sn→NC⋯sm→NC⋯,动作NC在路径上经常次执行,这个路径就叫做无条件公平路径
- 公式:
true⇒∀k⩾0,∃j⩾k,αj∈A
对轨迹中的动作序列的任一位置k,总能在k上或k后面找到一个位置j,该位置的动作αj∈A
-
强公平性(Strongly A-fair):若轨迹满足强公平性约束,如果A中存在的动作无限经常次想要执行,则会导致A中存在一个或多个动作可以无限经常次执行。
- 公式:
(∀k⩾0,∃j⩾k,Act(sj)∩A=∅)⇒∀k⩾0,∃j⩾k,αj∈A
对轨迹中的状态序列的任一位置k,若总能在k上或k后面找到一个位置j,使得状态sj的所有直接动作Act(sj)中存在A中的动作(即Act(sj)∩A=∅,无限经常次想要执行),那么A中一定存在无限经常次执行的动作
-
弱公平性(Weakly A-fair):若轨迹满足弱公平性约束,如果A中的某时刻开始,无限经常次有A中的动作想要执行,则会导致A中存在一个或多个动作可以无限经常次执行。
- 公式:
(∃k⩾0,∀j⩾k,Act(sj)∩A=∅)⇒∀k⩾0,∃j⩾k,αj∈A
对轨迹中的状态序列的某一位置k,若总能在k上或k后面找到一个位置j,使得状态sj的所有直接动作Act(sj)中存在A中的动作(即Act(sj)∩A=∅,无限经常次想要执行),那么A中一定存在无限经常次执行的动作
其中,Act(s)={α∈Act∣∃s′∈S,s→αs′}
-
例题一:
- 取动作A={enter1,enter2},判断下面的红色轨迹是否满足强公平性?(红色轨迹从第2个位置开始,234位置的状态轮以闭圈的形式无限次执行)
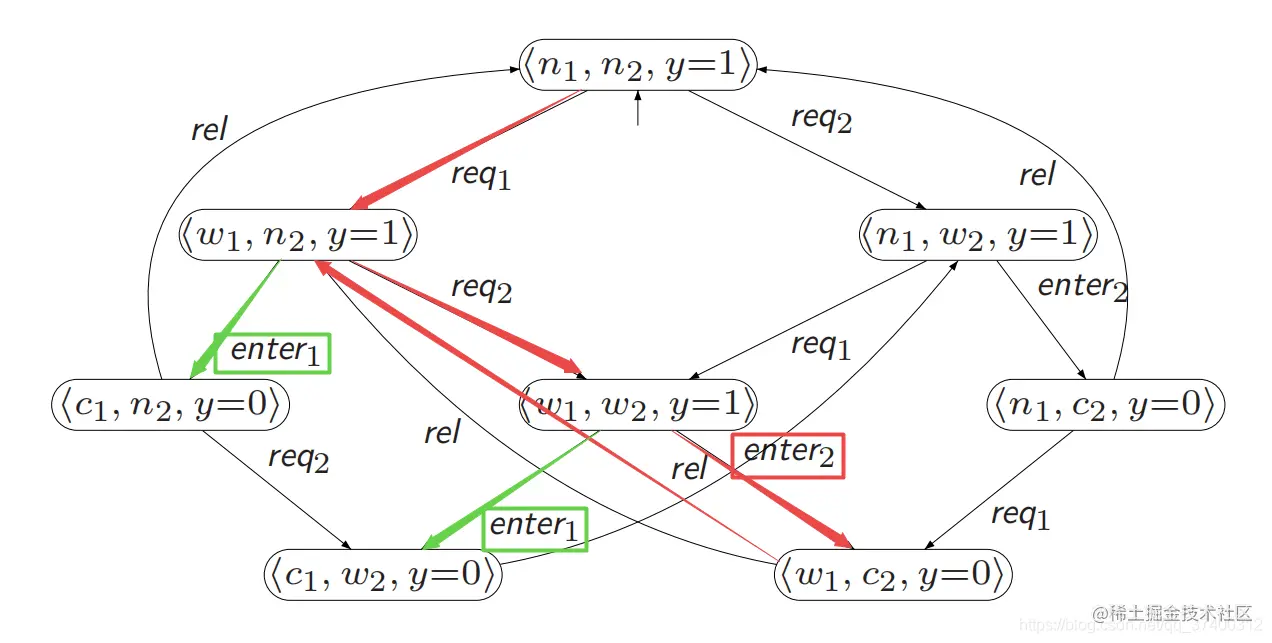
- 答案:
- 在红色轨迹中,我们看到,状态⟨w1,n2,y=1⟩无限次想要执行enter1,状态⟨w1,w2,y=1⟩无限次想要执行enter1和enter2,轨迹最终的结果是无限经常次执行enter2,所以这个轨迹满足强公平性。
-
例题二:
-
程序或进程在无条件公平性下终止的情况:
proc Inc =proc Reset = while ⟨x⩾0 do x:=x+1⟩ od x:=−1
x是共享变量,初始值为0
-
公平性对路径的约束过强或过弱
- 公平性的目的是排除“不合理”的路径,但如果我们去除了过度或者取出不足时,对验证结果会产生一定的影响。
- 约束过强(去除过度时):
- 总的路径⊆合理的路径⊆验证用的路径
- 如果验证结果为false,则可以说明合理的路径对应的模型是有问题的
- 如果验证的结果为true,无法说明合理的路径对应的模型是正确的
- 约束过弱(去除不足时):
- 总的路径⊆验证用的路径⊆合理的路径
- 如果验证结果为true,则可以说明合理的路径对应的模型是正确的
- 如果验证的结果为false,无法说明合理的路径对应的模型是错误的
关于公平性的这部分,我在另一篇文章里进行了讲解,但为了方便理解关于LTL的公平性约束问题,我有将这部分内容重新粘贴了过来,另一篇文章的链接为:blog.csdn.net/qq_37400312…
LTL的公平性约束
假设ϕ和ψ是在AP上的命题逻辑公式,则
- 无条件的LTL公平性约束的形式如下:ufair=□◊ψ
- 强LTL公平性约束的形式如下:sfair=□◊ϕ→□◊ψ,从此刻起每时每刻都会想要在未来某时刻想要执行ϕ,则从此刻起每时每刻都会能够在未来某时刻能够执行ψ
- 弱LTL公平性约束的形式如下:wfair=◊□ϕ→◊□ψ,在未来某一时刻起会一直想要执行ϕ,则在在未来某一时刻会一直能够执行ψ
ϕ表示想要执行,ψ表示能够执行
LTL的公平性假设
- 强公平性假设:sfair=0<i⩽k⋃(□◊ϕi→□◊ψi)
- 通用格式:fair=ufair∧sfair∧wfair
- 经验法则:强或无条件公平性假设有利于解决争议,弱的公平性足以解决由交织产生的不决定性
计算树逻辑( Computation tree logic,简称CTL)
线性时态逻辑和分支时态逻辑
- 线性时态逻辑:以状态开始的(所有)路径的语句。例如:
- s⊨□(x⩽20),表示从s开始的所有路径都满足x⩽20
- 分支时态逻辑:关于以一个状态开始的所有或某些路径的语句。例如:
- s⊨∀□(x⩽20),表示从s开始的所有路径都满足x⩽20
- s⊨∃□(x⩽20),表示从s开始存在路径满足x⩽20
检查LTL中是否有∃φ,可以用CTL的∀¬φ检测
转移系统(Transition systems)到树(Trees)的转换
Transition systems:
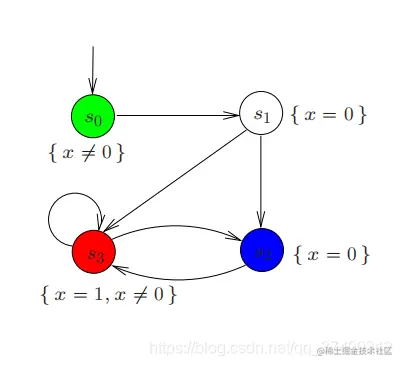 Trees:
Trees:
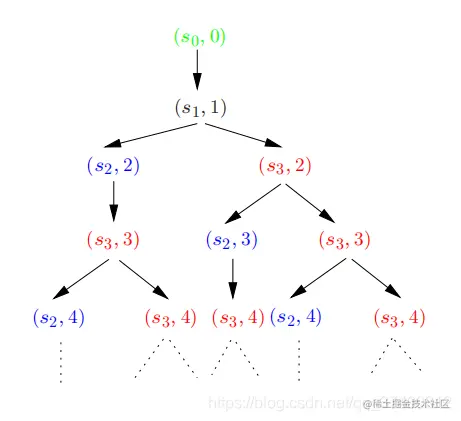 我们看到,这个Transition systems有着无穷无尽的路径,我们用数来表示各个路径,但没有办法将其全部表示出来,图中表示了前四次转移,虽然没有办法全部表示,但我们可以根据Transition systems来判断某条路径是否满足某性质。
我们看到,这个Transition systems有着无穷无尽的路径,我们用数来表示各个路径,但没有办法将其全部表示出来,图中表示了前四次转移,虽然没有办法全部表示,但我们可以根据Transition systems来判断某条路径是否满足某性质。
状态和算子
- 状态上的语句:
- 原子命题:a∈AP
- 否定律:¬ϕ
- 结合律:ϕ∧ψ
- 存在一条实现ϕ的路径:∃ϕ
- 所有路径都可以实现ϕ:∀ϕ
- 路径上的语句:
- 下一个状态满足:◯ϕ
- ϕ一直满足直到ψ满足:ϕ⋃ψ
◯和⋃会与∃和∀交替使用
- 派生算子:
- 存在路径满足ϕ:∃◊ϕ≡∃(true⋃ϕ)
- 所有路径满足ϕ:∀◊ϕ≡∀(true⋃ϕ)
- 存在路径总是满足ϕ:∃□ϕ≡¬∀◊¬ϕ
- 所有路径总是满足ϕ:∀□ϕ≡¬∃◊¬ϕ
- 弱直到:
∃(ϕWψ)≡¬∀((ϕ∧¬ψ)⋃(¬ϕ∧¬ψ))
∀(ϕWψ)≡¬∃((ϕ∧¬ψ)⋃(¬ϕ∧¬ψ))
语义
语义学的可视化化
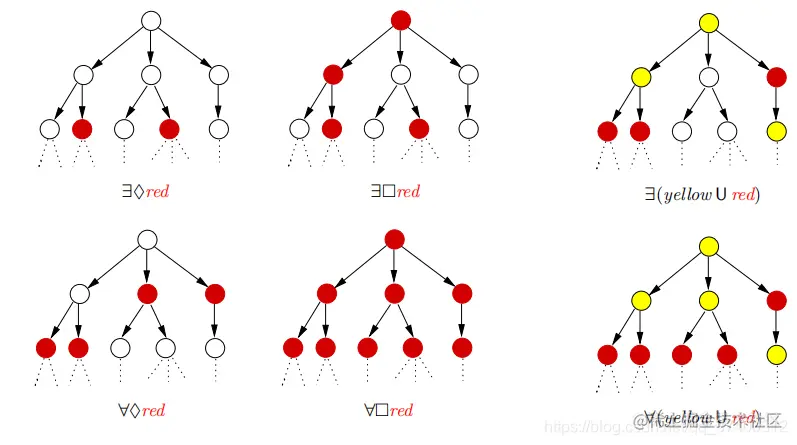
CTL状态公式的语义学
s⊨ϕ表示当且仅当公式ϕ在状态s中成立
- s⊨a,在a属于从状态s出发的路径中的一条路径时,时成立,即a∈L(s)
- s⊨¬ϕ,iff ¬(s⊨ϕ)
- s⊨¬ϕ,iff (s⊨ϕ)(s⊨ψ)
- s⊨∃ϕ,iff 从s开始的一些路径π满足π⊨ϕ
- s⊨∀ϕ,iff 从s开始的所有路径π满足π⊨ϕ
CTL路径公式的语义学
π⊨ϕ表示路径π满足公式ϕ
- π⊨◯ϕiff π[1]⊨ϕ
- π⊨ϕ ⋃ψ iff (∃j⩾0.π[j]⊨ψ∧∀0⩽k<j.π[k]⊨ϕ)
π[i]表示在路径π上面的状态si
迁移系统语义
- 满足CTL状态公式ϕ的集合Sat(ϕ)定义为:Sat(ϕ)={s∈S∣s⊨ϕ}
- 当所有初始状态满足ϕ时,TS满足CTL公式:TS⊨ϕ iff ∀s0⊨ϕ
TS可能不满足ϕ也不满足¬ϕ,即TS⊭ϕ and TS⊭¬ϕ
CTL的一些常用性质
根据上图,我们可以推出这个TS的四个性质:
,但
Trees:
我们看到,这个Transition systems有着无穷无尽的路径,我们用数来表示各个路径,但没有办法将其全部表示出来,图中表示了前四次转移,虽然没有办法全部表示,但我们可以根据Transition systems来判断某条路径是否满足某性质。