本文已参与「新人创作礼」活动,一起开启掘金创作之路。
线性时间行为(Linear-Time Behavior)
- 路径和状态图
- TS的状态图记作G(TS),是顶点V=S和边E={(s,s′∈S×S∣s′∈Post(S)}的有向图(V,E),其中s表示所有的状态集合
- Post∗(s)表示从s出发,在状态图G(TS)中可达的状态。
- 路径符号:有限路径π、无限路径π、从状态s出发的所有路径记为Paths(s),所有有限长的路径记为Pathsfin(s)
- 对于TS的路径是有限路径
- 轨迹(traces)
- 定义:一个TS系统可以用一系列轨迹来描述其行为的每一步,具体是,轨迹被定义为一串接连到达的状态si的标签函数L(si)的序列。因为L∈2AP,所以迹上的每个元素也是AP的子集。
- 对于状态图上的一系列转移可以记作为路径:s0→α0s1→α1s2,⋯,简写为:s0s1s2⋯,对其中每个结点对应的状态用标签函数映射到2AP上,得到的就是一个轨迹,可以用标签函数L(s0)L(s1)L(s2)⋯表示,这个轨迹的形式可以为:{a},{a,b},∅,⋯,其中a,b∈AP
- 路径长度:一个状态s0也可以叫做路径,比如{s0},它的路径长度为1。对于两个状态的路径{s0s2},它的的路径长度为2。
- 轨迹和轨迹片段
- TS=(S,Act,→,I,AP,L)是一个没有终止状态的TS
- 它的有限路径片段π=s0s1...,则轨迹被定义为trace(π)=L(s0)L(s1)...
- 它的无限路径片段π=s0s1...sn,则轨迹被定义为trace(π)=L(s0)L(s1)...L(sn)
- trace(∏)={trace(π)∣π∈∏},表示每条路径的轨迹
- Traces(s)=trace(Paths(s)),表示从s开始的所有路径的轨迹
- Traces(TS)=s∈I⋃Traces(s),表示所有从TS的每个初始状态出发的所有路径对应的轨迹的集合
- Tracesfin(s)=trace(Pathsfin(s)),表示从s出发所有有限路径对应的轨迹的集合
- Tracesfin(TS)=s∈I⋃Tracesfin(s),表示从TS的每个初始状态出发的所有路径对应的轨迹的集合
- 例题一:
- 基于信号量的互斥示例
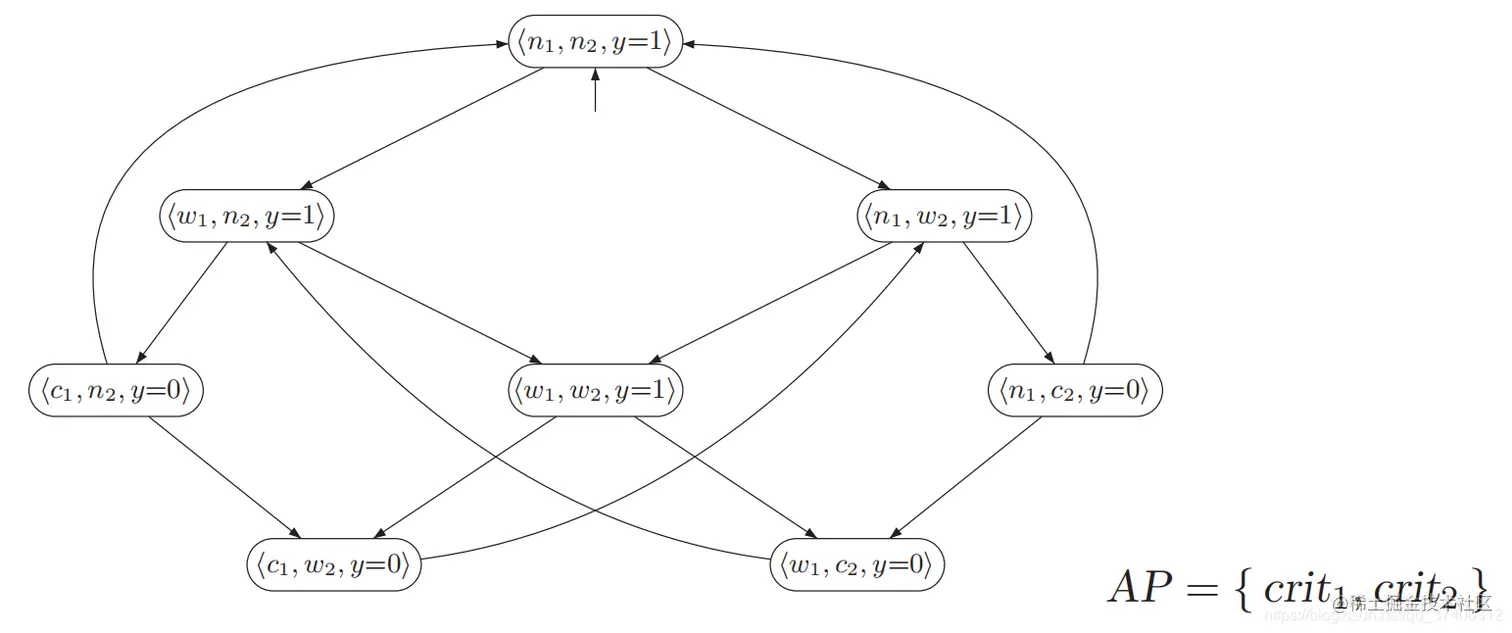 π=⟨n1,n2,y=1⟩→⟨w1,n2,y=1⟩→⟨c1,n2,y=0⟩→⟨n1,n2,y=1⟩→⟨n1,w2,y=1⟩→⟨n1,c2,y=0⟩→...
最多只能有一个进程处于临界区(crit1或crit2)
请给出有限路径π的轨迹
π=⟨n1,n2,y=1⟩→⟨w1,n2,y=1⟩→⟨c1,n2,y=0⟩→⟨n1,n2,y=1⟩→⟨n1,w2,y=1⟩→⟨n1,c2,y=0⟩→...
最多只能有一个进程处于临界区(crit1或crit2)
请给出有限路径π的轨迹
- 答案:trace(π)=∅∅{crit1}∅∅{crit2}∅∅{crit1}∅∅{crit2}....
- 解析:n表示noncrit,w表示wait,y表示锁,y=0表示“资源已上锁,不允许使用资源”,y=1表示“资源未上锁,可以使用资源”;对轨迹的解释:⟨n1,w2,y=1⟩表示第一个信号量的状态不处于临界区,第二个信号量的状态处于等待状态,没有锁,此时轨迹为∅,⟨c1,n2,y=1⟩表示第一个信号量的状态处于临界区,第二个信号量的状态不处于临界区,有锁,此时轨迹为crit1。每一个⟨⟩内状态的转变都都应一个轨迹碎片(轨迹碎片只能是:∅,{crit1},{crit2}当中的一个)。
有限字和无限字
- 对于原子命题集合AP={a,b},则2AP是AP的幂集:2AP={∅,{a},{b},{a,b}}
- 如果用(2AP)ω表示以2AP中元素为字母构成的所有无限长的字符集合,称为2AP上的无限字集合,这个集合可以表示为:
(2AP)ω={}{a}{b}{a,b}{a,b}...,∅∅{a,b}{a}...,∅{a}∅{a}∅{a}...,...
- 如果用(2AP)∗表示以2AP中元素为字母构成的所有有限长的字符集合,称为2AP上的有限字集合,这个集合可以表示为:
(2AP)∗={}{a}{b}{a,b}{a,b},∅∅{a,b}{a},∅{a}∅{a}∅{a},{a},∅∅,...
无限字集合和有限字集合中的元素数目都是无限多的
线性时间性质(Linear-Time Property,或写作LT性质)
- 定义:线性时间性质指定了TS展开后得到的轨迹,指定了系统可接受或期望接受的行为。
- 当且仅当TS内所有轨迹都在线性时间性质内(或者说TS上所有轨迹都含于P)时,TS满足线性时间性质P成立,即:
TS⊨PiffTraces(TS)⊆P
- 下面是两个进程对一个互斥信号量资源使用的例子:
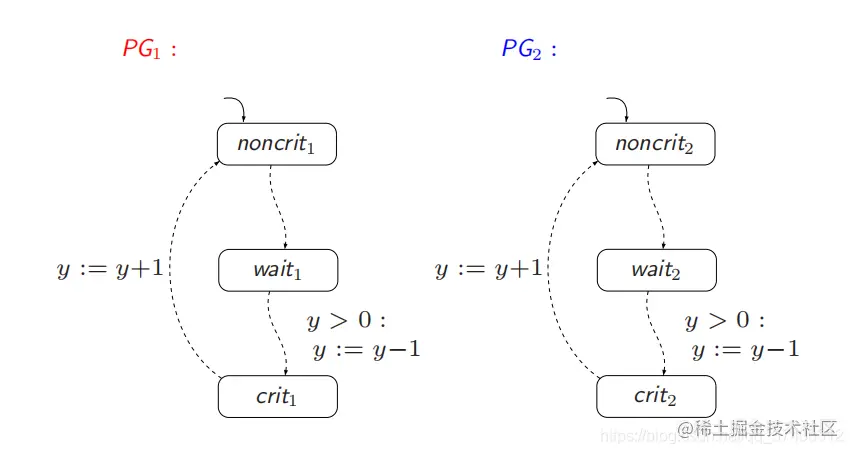 他们并发转换为TS后的结果:
他们并发转换为TS后的结果:
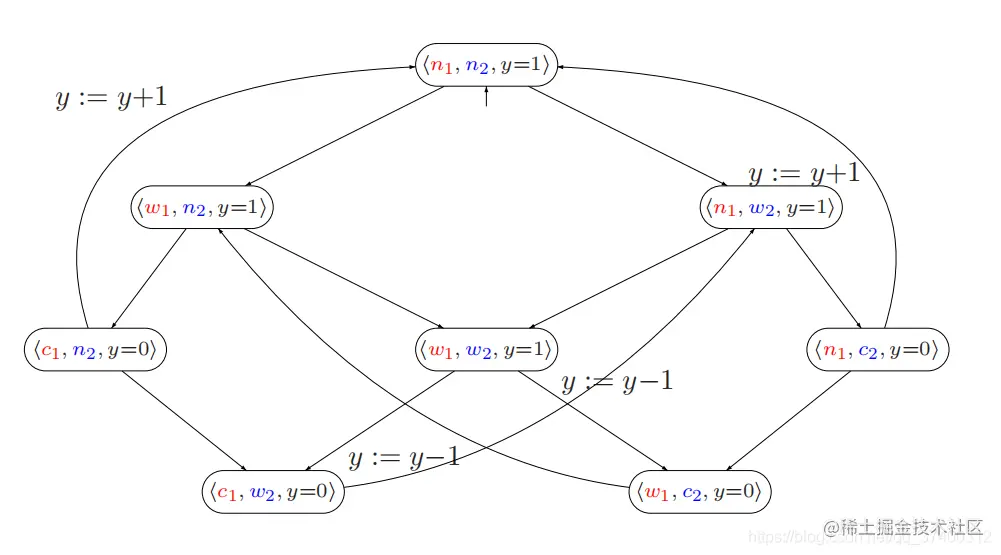 每个状态都是由之前两PG的Loc和互斥信号量y的取值组成,其中红色和蓝色分别表示两个进程的Loc,n表示在非临界区,w表示想要进入临界区,c表示正处在临界区,y=0表示“资源已上锁,不允许使用资源”,y=1表示“资源未上锁,可以使用资源”;
每个状态都是由之前两PG的Loc和互斥信号量y的取值组成,其中红色和蓝色分别表示两个进程的Loc,n表示在非临界区,w表示想要进入临界区,c表示正处在临界区,y=0表示“资源已上锁,不允许使用资源”,y=1表示“资源未上锁,可以使用资源”;
- LT Property的互斥性:
- 定义:至多只有一个进程进入临界资源。
- 解释:原子命题集合AP={crit1,crit2},两进程P1和P2处在访问临界资源状态,但他们永远至多只有一个进程进入临界资源,这一LT Property可表示为:Pmutex=对于无限字A0A1A2⋯的集合,对于所有0⩽i都有{crit1,crit2}⊈Ai
- 举例:像{crit1}{crit1}{crit2}...,∅{crit2}∅{crit1}...,∅∅∅...,...}都是合法的,但{crit1,crit2}这种无限字如果出现在集合中就是非法的,因为crit1和crit2是互斥的,不能同时发生,所以像{∅{crit2,crit1}{crit2}...}这样的轨迹就是非法的
- LT Property的无饥饿性:
- 定义:一个想访问临界资源的进程最终一定能访问到临界资源。
- 解释:原子命题集合AP={wait1,crit1,wait2,crit2}, 对于不但要满足“至多只有一个进程进入临界资源”,还要满足“一个想访问临界资源的进程最终一定能访问到临界资源”的情况,LT Property可表示为:Pmutex=对于无限字A0A1A2⋯的集合,对于每一个0∈{1,2}都有(∃∞j. waiti∈Aj)⇒(∃∞j. criti∈Aj)
- 举例:对每个进程Pi,当waiti无限经常次属于Aj时,那么criti就无限经常次属于Aj。也叫做“无限经常次想要,最终会导致无限经常次获得”,这就是无饥饿性。
∃∞表示无规律地无限经常次
轨迹的等效性和线性时间性的关系(Trace equivalence and Linear-Time properties)
- 对于在同一个原子命题集AP上的转移系统:TS和TS′,他们的轨迹集合可能存在以下两种关系:
if and only iffor any LT property P:TS′⊨P implies TS⊨P
- 解释:当且仅当对于任意线性时间性质$P$都有:$TS' \models P$则$TS \models P$成立时,$Traces(TS) \subseteq Traces(TS')$成立。换句话说就是,当$Traces(TS) \subseteq Traces(TS')$且$TS' \models P$时,$TS \models P$。
- 含义:一个$TS$扩张了另一个$TS$的实现
if and only ifTS and TS′ satisfy the same LT properties
- 解释:当且仅当两个$TS$满足相同的$LT$属性时,这两个$TS$从$TS$初始状态出发的所有路径的轨迹都相互包含。
- 含义:两个$LT$属性相同的系统的轨迹也是一致的。
Traces(TS)=Traces(TS′)中的“=”在这里表示相互包含的意思
不变性(Invariants)
-
含义:在原子命题集AP上,TS的每一个状态都要满足的性质,这个性质叫做不变性,用Pinv表示。
-
公式表示:Pinv={A0A1A2...∈(2AP)ω∣∀j⩾0.Aj⊨Φ}
-
公式解释:对于无限字集合中的每个字(也就是AP的子集)A0A1A2...都能满足Φ,则该LT property具有不变性。
Φ是AP上的命题逻辑公式,叫做Pinv的不变条件
-
TS⊨Pinv表示TS满足某一不变性质Pinv,和下面三个命题等价:
- 对TS的所有无限长的路径trace(π)都有:trace(π)∈Pinv
- 对TS的所有路径上的所有的状态s都有:L(s)⊨Φ
- 对TS的所有可达状态s都有:L(s)⊨Φ
- Φ必须满足所有的初始状态,并且Φ的满足性在TS的可达片段中的所有转移下是不变的
- 不变性性质只有一个不变性条件Φ是可定制的,也就是一个Φ即可决定整个不变性性质。
- 对不变性的检查只需搜索(如深度优先遍历)整个TS的图结构,看看每个结点状态是不是都满足Φ,而不需要真的找出所有的无限路径。
安全性(Safety Properties)
- 定义:在TS的有限路径上,坏的情况永远不会出现。记作Psafe
- 生活实例:比如一个ATM取款机,只有当输入了正确的PIN码后,才能取出现金,或者说,一栋房子,永远不会起火。如果房子永远不起火,则满足安全性,但如果未来某一天起火了,则违背了安全性。
- 安全性和不变性的区别:安全性是有限路径上每一个状态的性质,不变性是一条路径的性质,所有的不变性都属于安全性。
- 在AP上Psafe满足安全性的情况:对于所有σ∈(2AP)ω或σ∈Psafe,都存在有限的前缀σ,例如
Psafe∩{σ′∈(2AP)ω∣σ是σ′的一个前缀}
- 坏前缀(bad prefix):在有限路径上出现了坏的有限字σ,则违背了安全性,这个坏的有限字叫做Psafe的坏前缀,所有的坏的有限前缀的集合叫做BadPref(Psafe)。
- 最小坏前缀(minimal bad prefix):σ∈BadPref(Psafe),而且σ不是BadPref(Psafe)内任何片段的前缀。
判断坏前缀是否为最小坏前缀的时候,将坏前缀最后面的状态删除,如果删除后满足安全性,则为最小坏前缀,如果仍然为坏前缀,那么原式不是最小坏前缀。
- 例题二:
- 红灯(red)亮起前,必须有黄灯(yellow)亮起
- 对于无限字σ=A0A1A3...,若red∈Ai,则意味着,i的值大于零,且yellow∈Ai−1
- AP={red,yellow}
- 请观察下面几个有限字那些为最小坏前缀,那些为坏前缀,并画出相应的自动机
- ∅∅{red}
- ∅{red}
- {yellow}{yellow}{red}{red}∅{red}
- 答案:
- ∅∅{red}为最小坏前缀
- ∅{red}为最小坏前缀
- {yellow}{yellow}{red}{red}∅{red}为坏前缀,但并不是最小坏前缀,因为上述有限字还可以缩小为{yellow}{yellow}{red}{red}
- 自动机:
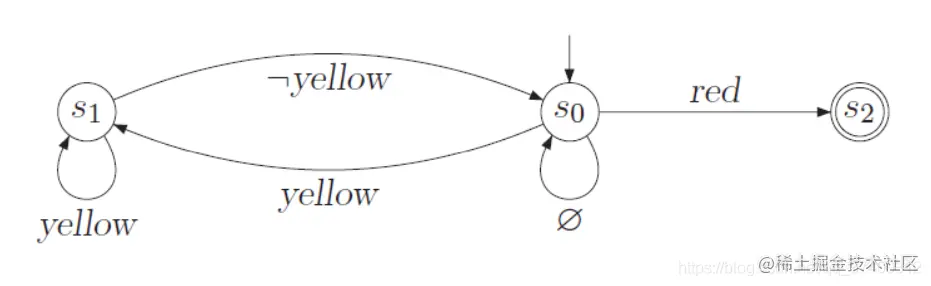
图中的¬yellow表示下一动作不是yellow时执行,不是yellow的话,可以是red,green
- 例题三:
- 自动售货机中,投入币的次数是至少是推出饮料的次数
- 对于无限字σ=A0A1A3...,满足∣{0⩽j⩽i∣pay∈Aj}∣≥∣{0⩽j⩽i∣drink∈Aj}∣
- AP={pay,drink}
- 请观察下面几个有限字那些为最小坏前缀,那些为坏前缀
- ∅{pay}{drink}{drink}
- ∅{pay}{drink}{drink}{drink}
- ∅{pay}{drink}∅{pay}{drink}{drink}
- 答案:
- ∅{pay}{drink}{drink}投入一次硬币推出两次饮料,不符合题目,为坏前缀,又无法再缩小,所以为最小坏前缀
- ∅{pay}{drink}{drink}{drink}投入一次硬币推出三次饮料,不符合题目,为坏前缀,可以删去最后一个{drink},依然为坏前缀,因此不是最小坏前缀
- ∅{pay}{drink}∅{pay}{drink}{drink}投入一次硬币推出一次饮料,然后投入一次硬币推出两次饮料,不符合题目,为坏前缀,又无法再缩小,所以为最小坏前缀
- 对于没有结束状态和安全性Psafe的转移系统TS有:
TS⊨Psafe等价于Tracesfin(TS)∩BadPref(Psafe)=∅
解释:Tracesfin(TS)∩BadPref(Psafe)=∅换一种表示形式为:Tracesfin(TS)⊆Pref(Psafe)
上面的等价公式的意思就是,对于TS系统和Psafe性质而言,只有在TS的有限轨迹含于Psafe的前缀,即Tracesfin(TS)⊆Pref(Psafe)时,TS才能够推出Psafe性质
闭包(Closure)
- 定义:轨迹σ∈(2AP)ω,pref(σ)为有限前缀集合,则pref(σ)={σ∈(2AP)∗∣σ是σ的一个有限前缀}
- 范例:σ=A0A1...那么pref(σ)={ε,A0,A0A1,A0A1A2,...}
ε表示为空
- 定义LT的性质P的前缀,为所有无限字的前缀集合的并集:pref(P)=σ∈P⋃pref(σ)
那么,LT的性质P的闭包定义为前缀都在pref(P)中的那些无限字的集合(得到的还是一个LT性质):
closure(P)={σ∈(2AP)ω∣pref(σ)⊆pref(P)}
也就是说,P的闭包是那些前缀也是P的前缀的无限字的集合。
反过来看,P的闭包中的无限字不会以不是P的前缀的有限字为前缀。
- 作用:使用闭包可以判定一个LT性质是不是安全性。一个LT性质是安全性,当且仅当其闭包是其本身:closure(P)=P
活性(liveness)
- 定义:安全性是坏的事情不会出现,而活性则是指好的事情终会出现;安全性是在有限的路径内成立,而活性则是在无限的路径内成立。
- 活性的前缀集合表示:Pref(Plive)=(2AP)∗
Pref(Plive)=(2AP)∗等价于closure(Plive)=(2AP)ω
- 活性分为三种:
- 无限次(Eventually):每个进程最终都会进入它的临界资源。
- 无限经常次(Repeated eventually):每个进程都会无限经常次进入临界资源。
- 饥饿情况(Starvation freedom):每一个等待进程(指想要访问临界资源的进程)最终都会进入临界资源。
非安全性也非活性的例子:
- 若定义LT性质为P⊂(2AP)ω ,则安全性和活性是不相交的。
- 若定义LT性质为P⊆(2AP)ω ,则仅有(2AP)ω既是安全性又是活性。这可由“安全性的闭包是其自身,而活性的闭包是整个无限字”来验证。
- 并非所有LT性质都是安全性或者活性,但总能表示成一个安全性和一个活性的合取形式。
- 例如【一个机器初始吐出三瓶雪碧,接下来可以无限经常次地吐出啤酒】,这一用自然语言描述的性质。仅看前半句是安全性(因为能用坏前缀表述,如前三个至少有一个是啤酒,那么就是一个坏前缀);仅看后半句是活性(注意,无限经常次吐出啤酒,并非是仅允许吐出啤酒,任何有限序列都无法说明是不是无限经常次吐出啤酒,这部分是活性)。
- LT性质的分类:
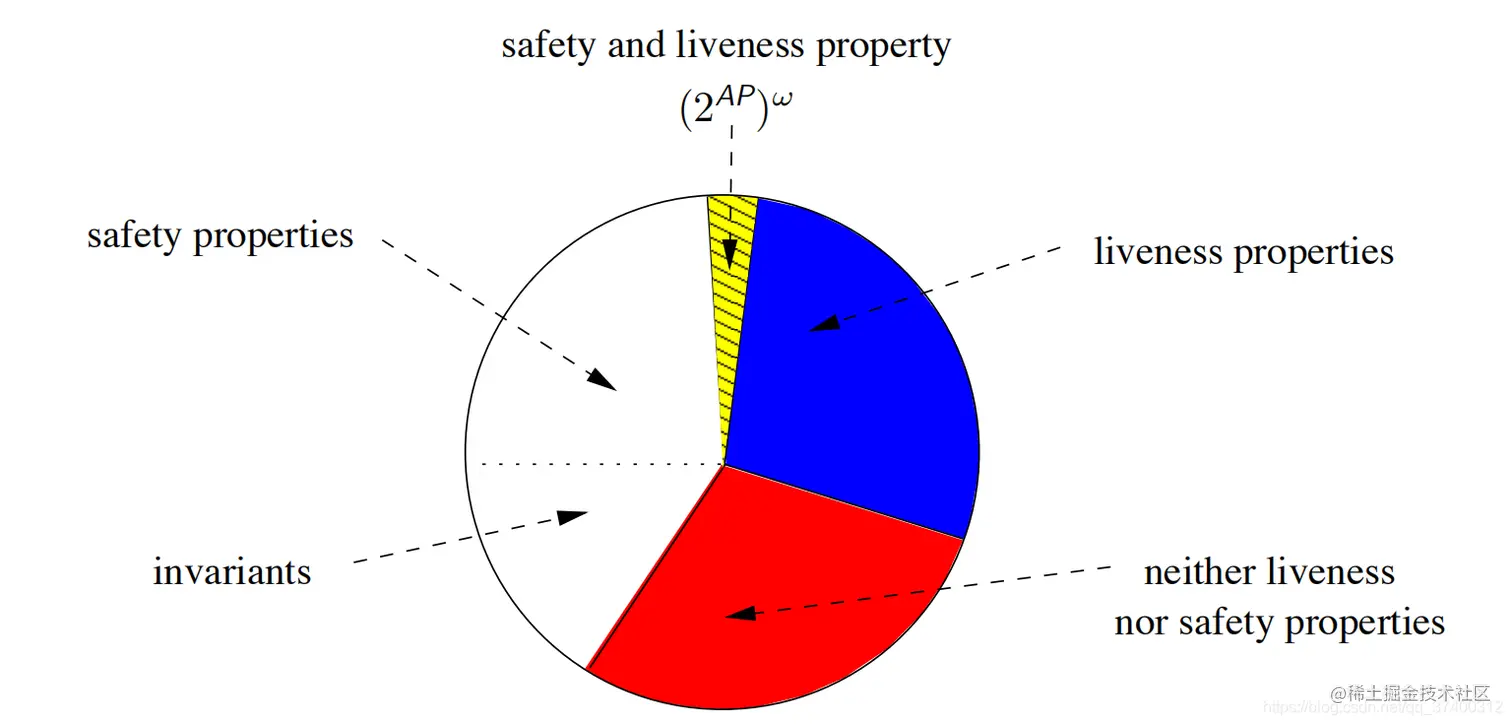
- invariants不变性
- safety properties安全性
- liveness properties活性
- safety and liveness property既是安全性又是活性
- neither liveness nor safety properties既不是安全性又不是活性
- 分解定理(Decomposition theorem):任何一个LT性质总能分解成安全性和活性的交集:P=Psafe∩Plive
- 一般地,因为闭包的闭包仍是自身(一定是安全性),总可以将其按闭包分解出来:P=closure(P)∩(P∪((2AP)ω∖closure(P)))
∖closure(P)表示去掉坏前缀
- 例题四:
Inc∣∣∣Resetwhereproc Inc=while(x⩾0 do x:=x+1)odproc Reset=x:=−1
x是一个共享整数变量,初始值为0
程序是否会终止?
- 答案:
Inc∣∣∣Reset表示进程Inc和进程Reset同时执行
proc Inc=while(x⩾0 do x:=x+1)od表示进程Inc的执行操作是:当x大于等于0时,x增加1
proc Reset=x:=−1表示进程Reset的执行操作是:对x赋值为-1
因为在计算机内,不会永远执行进程lnc,所以进程Reset一定会有执行的时候,当执行进程Reset后,x的值变为-1,因此进程lnc循环会结束,程序会终止
公平性(Fairness)
proc Inc =proc Reset = while ⟨x⩾0 do x:=x+1⟩ od x:=−1
x是共享变量,初始值为0
- 公平性对路径的约束过强或过弱
- 公平性的目的是排除“不合理”的路径,但如果我们去除了过度或者取出不足时,对验证结果会产生一定的影响。
- 约束过强(去除过度时):
- 总的路径⊆合理的路径⊆验证用的路径
- 如果验证结果为false,则可以说明合理的路径对应的模型是有问题的
- 如果验证的结果为true,无法说明合理的路径对应的模型是正确的
- 约束过弱(去除不足时):
- 总的路径⊆验证用的路径⊆合理的路径
- 如果验证结果为true,则可以说明合理的路径对应的模型是正确的
- 如果验证的结果为false,无法说明合理的路径对应的模型是错误的
公平性假设
- 公平性假设F将无条件公平、强公平性、弱公平性分属成三个集合,表示为三元组:F=(Fucond,Fstrong,Fweak)
- 其中
Fucond={fucond1,fucond2,⋯},{fstrong1,fstrong2,⋯},{fweak1,fweak2,⋯}
fucondi,fstrongi,fweaki⊆2Act
因此Fucond,Fstrong,Fweak⊆2Act
F=(∅,{{enter1},{enter2}},{{req1},{req2}})
需要考察每一个公平性属性,才能知道上图中的执行是否满足公平性假设F
- fstrong1={enter1}是满足的,因为enter1无限经常次使能且无限经常次进入了。
- fstrong2={enter2}是不满足的,因为其中的全部动作enter2没有无限经常次想要执行,所以也不用看有没有无限经常次执行了。
- fweak1={req1}是满足的,因为状态⟨n1,n2,y=1⟩无限次想要执行req1,并且执行力无限次,所以这条轨迹满足A=req1的弱公平性fweak1。
- fweak2={req2}是不满足的,虽然轨迹中的每个状态都想要执行req2,但在轨迹中并没有A=req2中无限经常次执行的动作。
最多只能有一个进程处于临界区(或) 请给出有限路径的轨迹
他们并发转换为后的结果:
每个状态都是由之前两的和互斥信号量的取值组成,其中红色和蓝色分别表示两个进程的,表示在非临界区,表示想要进入临界区,表示正处在临界区,表示“资源已上锁,不允许使用资源”,表示“资源未上锁,可以使用资源”;