本文已参与「新人创作礼」活动，一起开启掘金创作之路。

定义

• $Channel \ System($通道系统，简称$CS)$的状态有：$l_1, . . . , l_n, \eta , \xi$
  • $\eta$表示跟踪变量的当前值
  • $\xi$表示记录各种通道的当前内容
  • $l_i \in Loc_{0,i}$表示初始条件，变量$\eta$必须满足初始条件$g_{0,i}$
  • 如果初始通道为空，则表示为$\xi_0(c) = \varepsilon$
• 公式定义：
  • 通道系统$CS = |PG_1|...|PG_n|$是一个在通道和变量（$Chan,Var)$上基于$PG_i=(Loc_i,Act_i,Effect_i,\hookrightarrow_i,Loc_{0,i},g_{0,i} )$的系统，其中，$0 < i \leq n$
  • $CS$的$TS$表示为一个元组：$TS(CS)=(S,Act,\to,I,AP,L)$
    • $S = (Loc_1 \times ... \times Loc_n) \times Eval(Var) \times Eval(Chan)$
    • $Act=\uplus_{0<i \leq n}Act_{i} \ \uplus \ \tau$
    • $I = \begin{Bmatrix} \left \langle l_1,l_2,...,l_n,\eta,\xi_0 \right \rangle | \forall 0<i \leq n(l_i \in Loc_{0,i} \wedge \eta )\models g_{0,i} \end{Bmatrix}$
    • $AP=\uplus_{0<i \leq n}Loc_i \uplus Cond(Var)$
    • $L( \left \langle l_1,l_2,...,l_n,\eta,\xi \right \rangle )=\{l_1,..,l_n \} \cup {g \in Cond(Var)|\eta \models g}$
    • $\to$表示进行转移，总共有三种转移情况：
      • 对于$Interleaving$（交错）的情况，当$\alpha \in Act_i$时，表示每一个$l_i$进行各自的转移

$\tfrac {l_{1} \xhookrightarrow[]{g : \alpha }_{1}{l_{1}'} \ \wedge \ \eta \models g} {\langle l_{1},l_{2},...,l_i,...,l_n,\eta,\xi \rangle \overset{\alpha}{\rightarrow} \langle l_{1},l_{2},...,{l_i}',...,l_n,{\eta}',\xi' \rangle }$

其中${\eta}'=Effect(\alpha,\eta)$ - 在异步通信中，$cap(c)>0,(c \in Chan)$ - 沿通道$c$接收一个值，并将其分配给变量$x$：

$\tfrac {l_{i} \xhookrightarrow[]{g : c?x }{l_i}' \wedge \eta \models len(\xi(c))=k>0 \wedge \xi(c)=v_1...v_k} {\langle l_{1},l_{2},...,l_i,...,l_n,\eta,\xi \rangle \overset{\tau}{\rightarrow} \langle l_{1},l_{2},...,{l_i}',...,l_n,{\eta}',\xi' \rangle }$

其中${\eta}′ = \eta[x := v_1]$ 且 ${\xi}′ = \xi [c := v_2 ...v_k]$ - 信道$c$上传输值$v$，且$v\in dom(C)$：

$\tfrac {l_{i} \xhookrightarrow[]{g : c!v }{l_i}' \wedge \eta \models len(\xi(c))=k<cap(c) \wedge \xi(c)=v_1...v_k} {\langle l_{1},l_{2},...,l_i,...,l_n,\eta,\xi \rangle \overset{\tau}{\rightarrow} \langle l_{1},l_{2},...,{l_i}',...,l_n,\eta,\xi' \rangle }$ 其中${\xi}′ = \xi [c := v_1 v_2 ...v_k v]$ > $len(\xi(c))=k$表示信道内消息的数量，如果$k>0$表示通道内有消息 - 在同步通信中，$cap(c)=0，(c \in Chan)$

$\tfrac {l_{i} \ \xhookrightarrow[]{g_1 : c?x } \ {l_i}' \ \wedge \ \eta \ \models \ g_1 \ \wedge \ \eta \ \models \ g_2 \ \wedge \ l_j \ \xhookrightarrow[]{g_2 : c!v } \ {l_j}' \ \wedge \ i \ \neq \ j} {\langle l_{1},l_{2},...,l_i,...,l_j,...,l_n,\eta,\xi \rangle \overset{\tau}{\rightarrow} \langle l_{1},l_{2},...,{l_i}',...,{l_j}',...,l_n,\eta',\xi \rangle }$ 其中${\eta}′ = \eta[x := v]$

应用：NanoPromela

• 介绍：NanoPromela是Promela语言的核心，用于SPIN工具进行模型检测，这种语言支持共享变量间的通信，支持同步或异步（缓冲区输入输出通道）进行消息传递，形式化语义可以通过通道系统($CS$)提供，通道系统可以展开为转移系统($TS$)。语言不指定使用动作名称，而是指定动作的效果。
• 简单的语法介绍：
  • $skip$表示跳转语句
  • $atomic$表示原子赋值
  • $do$表示循环语句
  • $\{\}$表示括号内所有变量赋值语句执行一遍
• 范例：

• NanoPromela实现彼得森互斥算法（peterson’s mutual exclusion algorithm）：

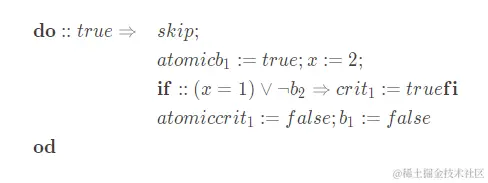
• NanoPromela实现自动售货机（peterson’s mutual exclusion algorithm）：

同步并行（Synchronous Parallelism）

• 解释：表示同时往前走，比如同步机的各项操作必须同步进行
• 公式定义：
  • 两个结构相同的$TS:TS_i = (S_i,Act,\to_i,I_i,AP_i,L_i),i=1,2$
  • $TS_i$具有相同动作集$Act$，$Act \times Act \to Act$。如果$\alpha$给$S_1$进行变换，$\beta$给$S_2$进行变换，那么$\alpha * \beta$表示在一次$Act$中同时给$S_1$和$S_2$变换
  • $TS_1 \otimes TS_1 = (S_1 \times S_2,Act,\to,I_1 \times I_2,AP_1 \cup AP_2,L)$

• $L(\left \langle S_1,S_2 \right \rangle) = L_1(S_1) \cup L_2(S_2)$
• 例题一：

  • 计算两条电路的同步乘积

  • 答案： 首先，分别计算两条电路的$TS$ 将$TS_1$和$TS_2$同步并行

状态爆炸问题（the State-Space Explosion Problem）

• 原因：每一个状态变量都有一定的取值范围，如果状态变量多了，状态变量之间的组合会更多，由此导致无法在有限的时间内求出预期结果
• 用$PG$表示为： $|Loc| \cdot \prod_{x \in Var} |dom(x)| \cdot$
• 用$CS$表示为： $\prod_{x \in Var}^{n}(|Loc| \cdot \prod_{x \in Var} |dom(x)| )\cdot \prod_{c \in Chan} |dom(x)|^{cp(c)}$