离心力和科里奥利力是怎么来的？

Phantomlsh
944 阅读6分钟

本文已参与「新人创作礼」活动，一起开启掘金创作之路。

离心力和科里奥利力都是惯性力，简单来说，是因为观测者所在的参考系本身在旋转（例如地球），从而使观测者产生“错觉”，认为物体受到额外的力。

向量与参考系

线性代数告诉我们，任意向量在三维空间内可以表示成一组基向量的线性组合：（此处基向量为正交单位向量i^,j^,k^\boldsymbol{\hat{i}}, \boldsymbol{\hat{j}}, \boldsymbol{\hat{k}}）

v=xi^+yj^+zk^\boldsymbol{v} = x\boldsymbol{\hat{i}} + y\boldsymbol{\hat{j}} + z\boldsymbol{\hat{k}}

基向量的本质是当前参考系的坐标轴，基向量前的系数即为观测者在这个参考系下测量向量v\boldsymbol{v}所得的向量坐标(x,y,z)(x,y,z)。

请注意，一个参考系的基向量本身也是向量，因此，我们可以考察一个参考系的基向量在另一个参考系下的运动情况。

根据牛顿第一定律，惯性参考系被定义为静止或匀速直线运动的参考系，因此在静止的参考系SS下观测另一个惯性参考系II，II的基向量不随时间变化，即对时间求导为00。

考虑一个观测者和他对应的参考系RR，RR在围绕静止参考系SS的zz轴以角速度Ω\Omega匀速旋转，也就是说，RR的三个基向量都以角速度Ω\Omega绕zz轴匀速旋转。

设静止参考系SS中的基向量为i^,j^,k^\boldsymbol{\hat{i}}, \boldsymbol{\hat{j}}, \boldsymbol{\hat{k}}，旋转参考系RR的基向量为i^′,j^′,k^′\boldsymbol{\hat{i}'}, \boldsymbol{\hat{j}'}, \boldsymbol{\hat{k}'}。

引理1

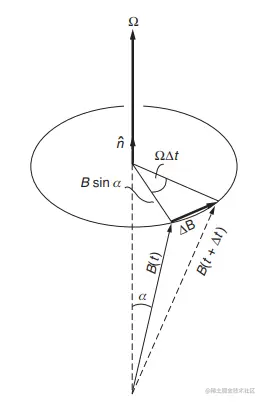
Screenshot 2022-04-06 5.25.35 PM.png

对于任意向量B\boldsymbol{B}，若其与zz轴夹角为α\alpha，并围绕zz轴以角速度Ω\Omega做匀速圆周运动（见上图），在极短时间Δt\Delta t内，我们有几何关系：

ΔB=ΩΔtR=ΩΔt∣B∣sin⁡α\boldsymbol{\Delta B} = \Omega \Delta t R = \Omega \Delta t |\boldsymbol{B}|\sin\alpha

在极短时间内，Δt→0\Delta t \to 0

dBdt=Ω∣B∣sin⁡α=Ω×B\frac{d\boldsymbol{B}}{dt} = \Omega |\boldsymbol{B}|\sin\alpha = \boldsymbol{\Omega}\times\boldsymbol{B}

特别注意，这个等式对于任意围绕zz轴旋转的任意向量B\boldsymbol{B}都成立，我们没有考虑任何与参考系有关的内容。

引理2

现在考虑两个参考系，第一个是静止的参考系SS，第二个是围绕zz轴以角速度Ω\Omega匀速转动的参考系RR，他们的基向量分别为i^,j^,k^\boldsymbol{\hat{i}}, \boldsymbol{\hat{j}}, \boldsymbol{\hat{k}}和i^′,j^′,k^′\boldsymbol{\hat{i}'}, \boldsymbol{\hat{j}'}, \boldsymbol{\hat{k}'}。

对于任意向量C\boldsymbol{C}，分别分解到两个坐标系的基向量上，有：

C=Cxi^+Cyj^+Czk^=Cx′i^′+Cy′j^′+Cz′k^′\boldsymbol{C} = C_x\boldsymbol{\hat{i}}+C_y\boldsymbol{\hat{j}}+C_z\boldsymbol{\hat{k}} = C_x'\boldsymbol{\hat{i}'}+C_y'\boldsymbol{\hat{j}'}+C_z'\boldsymbol{\hat{k}'}

请注意，我们将同一个向量分解到两组不同的基向量上，因此他们虽然系数和基向量不同，但线性组合的结果相同。

等式最左侧和最后侧同时对时间求导（上加一点表示对时间求一次导，由于求导的乘法法则，我们有六项）：

dCdt=C˙x′i^′+C˙y′j^′+C˙z′k^′+Cx′di^′dt+Cy′dj^′dt+Cz′dk^′dt\frac{d\boldsymbol{C}}{dt} = \dot C_x'\boldsymbol{\hat{i}'}+\dot C_y'\boldsymbol{\hat{j}'}+\dot C_z'\boldsymbol{\hat{k}'} + C_x'\frac{d\boldsymbol{\hat{i}'}}{dt}+C_y'\frac{d\boldsymbol{\hat{j}'}}{dt}+C_z'\frac{d\boldsymbol{\hat{k}'}}{dt}

此时在静止参考系SS中观察RR的基向量i^′,j^′,k^′\boldsymbol{\hat{i}'}, \boldsymbol{\hat{j}'}, \boldsymbol{\hat{k}'}，它们都在围绕zz轴匀速旋转，因此它们也满足引理1的作用条件。根据引理1，我们有

di^′dt=Ω×i^′dj^′dt=Ω×j^′dk^′dt=Ω×k^′\frac{d\boldsymbol{\hat{i}'}}{dt} = \boldsymbol{\Omega}\times\boldsymbol{\hat{i}'} \quad\frac{d\boldsymbol{\hat{j}'}}{dt} = \boldsymbol{\Omega}\times\boldsymbol{\hat{j}'} \quad\frac{d\boldsymbol{\hat{k}'}}{dt} = \boldsymbol{\Omega}\times\boldsymbol{\hat{k}'}

带入上面的六项中的后面三项，提取出Ω×\boldsymbol{\Omega}\times，我们得到

dCdt=C˙x′i^′+C˙y′j^′+C˙z′k^′+Ω×(Cx′i^′+Cy′j^′+Cz′k^′)\frac{d\boldsymbol{C}}{dt} = \dot C_x'\boldsymbol{\hat{i}'}+\dot C_y'\boldsymbol{\hat{j}'}+\dot C_z'\boldsymbol{\hat{k}'} + \boldsymbol{\Omega}\times(C_x'\boldsymbol{\hat{i}'}+C_y'\boldsymbol{\hat{j}'}+C_z'\boldsymbol{\hat{k}'})

我们发现最右侧的括号中的表达式，就是向量C\boldsymbol{C}本身！

dCdt=C˙x′i^′+C˙y′j^′+C˙z′k^′+Ω×C\frac{d\boldsymbol{C}}{dt} = \dot C_x'\boldsymbol{\hat{i}'}+\dot C_y'\boldsymbol{\hat{j}'}+\dot C_z'\boldsymbol{\hat{k}'} + \boldsymbol{\Omega}\times\boldsymbol{C}

以上全部的内容都是站在静止参考系SS当中讨论的，因此我们能知道RR的基向量在随时间发生变化。然而，对于站在参考系RR中的观测者来说，因为他随着参考系RR一起运动，RR的基向量i^′,j^′,k^′\boldsymbol{\hat{i}'}, \boldsymbol{\hat{j}'}, \boldsymbol{\hat{k}'}对于此观测者来说应该是静止的。在他的视角当中，导数六项中的后三项均为0。因此，（下标表示观测者本身所在的参考系）

(dCdt)R=C˙x′i^′+C˙y′j^′+C˙z′k^′\Big(\frac{d\boldsymbol{C}}{dt}\Big)_R = \dot C_x'\boldsymbol{\hat{i}'}+\dot C_y'\boldsymbol{\hat{j}'}+\dot C_z'\boldsymbol{\hat{k}'}

于是，我们总结一下，

(dCdt)S=(dCdt)R+Ω×C\Big(\frac{d\boldsymbol{C}}{dt}\Big)_S = \Big(\frac{d\boldsymbol{C}}{dt}\Big)_R + \boldsymbol{\Omega}\times\boldsymbol{C}

最后一项不需要下标，因为在任意参考系下，向量本身都是一致的。特别注意，这一等式对于空间中的任意向量C\boldsymbol{C}都成立，无论其运动情况如何。

旋转参考系下的运动学

由于引理2对任意向量成立，我们带入位置向量C→r\boldsymbol{C}\to\boldsymbol{r}，

(drdt)S=(drdt)R+Ω×r\Big(\frac{d\boldsymbol{r}}{dt}\Big)_S = \Big(\frac{d\boldsymbol{r}}{dt}\Big)_R + \boldsymbol{\Omega}\times\boldsymbol{r}

根据定义，在任意参考系下，位置向量对时间求导为速度向量：v=r˙\boldsymbol{v} = \dot{\boldsymbol{r}}，速度向量对时间求导为加速度向量：a=v˙=r¨\boldsymbol{a} = \dot{\boldsymbol{v}} = \ddot{\boldsymbol{r}}。因此我们找到了两个参考系下观测到的同一个质点的速度关系：（再次强调，下标表示观测者所在的参考系）

vS=vR+Ω×r\boldsymbol{v}_S = \boldsymbol{v}_R + \boldsymbol{\Omega}\times\boldsymbol{r}

我们再将vS\boldsymbol{v}_S（这还是一个向量）再次带入引理2，C→vS\boldsymbol{C}\to\boldsymbol{v}_S

(dvSdt)S=(dvSdt)R+Ω×vS\Big(\frac{d\boldsymbol{v}_S}{dt}\Big)_S = \Big(\frac{d\boldsymbol{v}_S}{dt}\Big)_R + \boldsymbol{\Omega}\times\boldsymbol{v}_S

此等式左侧即为在静止坐标系SS下观测到的加速度vS\boldsymbol{v}_S，右侧我们摒弃杂念带入关系vS=vR+Ω×r\boldsymbol{v}_S = \boldsymbol{v}_R + \boldsymbol{\Omega}\times\boldsymbol{r}

aS=(ddt(vR+Ω×r))R+Ω×(vR+Ω×r)\boldsymbol{a}_S = \Big(\frac{d}{dt}(\boldsymbol{v}_R + \boldsymbol{\Omega}\times\boldsymbol{r})\Big)_R + \boldsymbol{\Omega}\times(\boldsymbol{v}_R + \boldsymbol{\Omega}\times\boldsymbol{r})

整理一下，注意Ω˙=0\dot{\boldsymbol{\Omega}} = 0

aS=(dvRdt)R+Ω×(drdt)R+Ω×vR+Ω×(Ω×r)\boldsymbol{a}_S = \Big(\frac{d\boldsymbol{v}_R}{dt}\Big)_R+\boldsymbol{\Omega}\times\Big(\frac{d\boldsymbol{r}}{dt}\Big)_R + \boldsymbol{\Omega}\times\boldsymbol{v}_R + \boldsymbol{\Omega}\times(\boldsymbol{\Omega}\times\boldsymbol{r})

等式右侧的第一项根据定义为旋转参考系下观测到的加速度aR\boldsymbol{a}_R。第二项中的括号部分，根据定义为vR\boldsymbol{v}_R。将第二项及其后的部分移动到左侧，我们最终获得了

aR=aS−2Ω×vR−Ω×(Ω×r)\boldsymbol{a}_R = \boldsymbol{a}_S - 2\boldsymbol{\Omega}\times\boldsymbol{v}_R - \boldsymbol{\Omega}\times(\boldsymbol{\Omega}\times\boldsymbol{r})

让我们看看这个式子告诉我们什么。首先，对于同样一个质点，在两个参考系下观测到的加速度是不同的。为什么呢？显然是因为旋转参考系的观测者本身并不在惯性系下，然而他自己意识不到这一点。因此，他的观测和静止参考系下的观测会产生出入，这个出入就是等式右侧的第二项和第三项。

惯性力

由于牛顿第二定律F=ma\boldsymbol{F} = m\boldsymbol{a}只有在惯性系下有效，我们可以得到上述质点的净受力为

FS=maS\boldsymbol{F}_S = m\boldsymbol{a}_S

但是，站在旋转参考系RR中的观测者不知道这一点，他也尝试使用牛顿第二定律，于是他得到

FR=maR=maS−2mΩ×vR−mΩ×(Ω×r)\boldsymbol{F}_R = m\boldsymbol{a}_R = m\boldsymbol{a}_S - 2m\boldsymbol{\Omega}\times\boldsymbol{v}_R - m\boldsymbol{\Omega}\times(\boldsymbol{\Omega}\times\boldsymbol{r})

于是，对于一脸莫名其妙的旋转参考系观测者来说，就好像这个物体凭空受到了两个额外的力，它们被称为惯性力：

FR=FS+FCoriolis+Fcentrifugal\boldsymbol{F}_R = \boldsymbol{F}_S + \boldsymbol{F}_{Coriolis} + \boldsymbol{F}_{centrifugal}

其中：

  1. Fcentrifugal=−mΩ×(Ω×r)\boldsymbol{F}_{centrifugal} = -m\boldsymbol{\Omega}\times(\boldsymbol{\Omega}\times\boldsymbol{r})被称为离心力，因为两次叉乘因此永远垂直于转轴，所以只和质点所在的位置有关。因此在质点与观测者相对静止的情况下也存在离心力。
  2. FCoriolis=−2mΩ×vR\boldsymbol{F}_{Coriolis} = -2m\boldsymbol{\Omega}\times\boldsymbol{v}_R被称为科里奥利力，与物体在旋转参考系下的速度有关。最著名的例子是地理上的地转偏向力：因为地球本身是一个旋转参考系，因此在地球表面上运动的物体（相对于地面有速度vR\boldsymbol{v}_R）会受到额外的力。虽然地球的角速度极小，但是地转偏向力依然对河流等地质构造和大气环流有重大影响。

总结一下，离心力和科里奥利力本身并不是真实存在的力，而是由于观测者本身所在的参考系不是惯性参考系，观测者本身产生了“错觉”，认为物体凭空受到了额外的力。

作为来自地球这个巨大旋转参考系的原住民，物理帮助我们理解这一现象，使我们可以从一斑窥一豹！

图片来自An Introduction to Mechanics (Kleppner, Kolenkow)

avatar
文章
阅读
粉丝