本文已参与「新人创作礼」活动，一起开启掘金创作之路。

有一个自动售货机（Beverage Vending Machine），现在需要设计一个模型，计数苏打水（soda）和啤酒（beer）的数量，如果自动售货机是空的，则返回插入的硬币（coin）

• Data-Dependent Systems和TS模型不同的是，这里用位置（Location）替换TS的状态，用转移条件（Conditional transition）替换TS的转换关系。

对于自动售货机：

• 状态： start, select
• 条件转移：
  1. 从初始位置投入硬币后，转变为等待选择饮料位置 $start \xhookrightarrow[]{ture \ : \ coin} select$
  2. 从初始位置填满苏打和啤酒后，位置仍然为初始位置 $start \xhookrightarrow[]{ture \ : \ ture:refill} start$

start表示售货机处于初始位置 select表示售货机处于已完成投币，等待选择饮料的位置

转移条件$g:\alpha$

在自动售货机ture:coin和ture:refill，他们是转移条件，表示为$g:\alpha$

• $g$表示一个布尔状态
• $\alpha$表示一个动作，只有当$g$为true的时候，才会执行动作$\alpha$，否则什么也不会执行

我们可以再看一些其他的条件转移过程：

1. 当苏打饮料的数量大于0的时候，执行sget动作获取苏打饮料 $start \xhookrightarrow[]{nsoda \ > \ 0 \ : \ sget} start$
2. 当啤酒的数量大于0的时候，执行bget动作获取啤酒 $start \xhookrightarrow[]{nbeer\ > \ 0 \ : \ bget} start$
3. 当苏打饮料和啤酒的数量为空的时候，执行ret_coin动作退回投入的硬币 $start \xhookrightarrow[]{nsoda \ = \ 0 \wedge nbeer \ = \ 0 \ : \ ret \_coin} start$

不同动作产生的不同影响：

动作	说明	影响
coin	投入硬币	无
ret_coin	退回硬币	无
refill	重新填满苏打和啤酒	nsoda := max;nbeer := max
sget	获取一瓶苏打	nsoda := nsoda -1
bget	获取一瓶啤酒	nbeer := nbeer -1

nsode表示苏打的数量，nbeer 表示啤酒的数量

具备类型的变量（typed variable）

• 概念：一个标准化的类型（如整数、布尔值、字符等）将和变量相关联以对系统建模

• Var：前面的例子中 nsoda和nbeer都属typed variable，简称变量（Var）。

• dom(x)：每个变量x的取值范围记作域（dom）。对数字电路而言，变量的取值只能是0或者1，但对于软件而言，变量的取值范围可能非常大（如考虑程序内整数的范围），这时没法再用域做有效的限制，所以引出域的概念。对于n个变量$x = (x_{1},x_{2},...,x_{n})$，其域为$D = (D_{1}\times D_{2}\times ...\times D_{n})$

• Eval(Var)：对所有变量的定值，所有可能结果的集合记作Eval(Var)，其中的一种定值方式记作映射$\eta$，如对变量x的定值即记作 $\eta(x)$。

• Cond(Var)：在变量上设置的所有条件的集合，记作Cond(Var)

• Effect：动作对变量的影响是动作作用于变量原值，再得到变量新值的这样一个映射，即 $Act \times Eval(Var)→ Eval(Var)$

• 范例：以一个动作$\alpha : x:=y+5$为例，初始时对变量x和y的求值$\eta(x)=17，\eta(y)=-2$ 如果对x执行$\alpha$动作，则x的值最终等于y+5，也就是-2+5=3 $Effect(\alpha ，\eta )(x)=\eta(y)+5=−2+5=3$ 如果对y执行$\alpha$动作，因为$\alpha$只对x的值进行修改，不对y的值进行修改，所以y的值仍然为-2 $Effect(\alpha ,\eta )(y)=\eta (y)=−2$

程序图 (Program Graph，简称PG)

• 概念：有向图，连接不同结点的边被标记为变量和动作，结点标记为位置。
• 行动$action$的效果是通过映射来形式化的，比如上面具备类型的变量的那个范例：
  • $Effect :Act × Eval(Var) \hookrightarrow Eval(Var)$
  • $\alpha \ \ action \ \ x := y+5$
  • $\eta \ \ evaluation \ \ \eta(x) = 17 ， \eta(y) = −2$
  • $Effect(\alpha,\eta)(x)=\eta(y) + 5 =−2 + 5 = 3$
  • $Effect(\alpha,\eta)(y) =\eta(y) = −2$
• PG是一个六元组$PG = (Loc, Act, Effect, \hookrightarrow, Loc_{0}, g_{0})$
  • Loc是一系列位置的集合
  • Act是一系列动作的集合
  • Effect是$Act \times Eval(Var) \rightarrow Eval(Var)$
  • $\hookrightarrow \subseteq Loc \times Cond(Var) \times Act \times Loc$，是一个关系转移条件
  • $Loc_{0} \subseteq Loc$：是一系列初始位置的集合
  • $g_{0} \in Cond(Var)$：是一系列初始条件的集合
• 在之前的自动售货机的范例中
  • $Loc=\{start,select\}$
  • $Loc_{0}=\{start\} \ Var=\{ nsoda,nbeer\}$
  • $Act=\{bget,sget,coin,ret\_coin,refill\}$
  • $g_{0}=\{nsoda=max \wedge nbeer=max \}$ ，表示刚开始，苏打和啤酒的数量都是满的
  • $Effect：$
    • $Effect(coin,\eta) = \eta$，表示投入硬币，目标变量（nsoda和nbeer）没有改变
    • $Effect(ret_coin,\eta) = \eta$，表示退回硬币，目标变量（nsoda和nbeer）没有改变
    • $Effect(sget,\eta) = \eta[nsoda:=nsoda-1]$，表示获取一瓶苏打，nsoda的值减少一
    • $Effect(bget,\eta) =\eta[nbeer:=nbeer-1]$，表示获取一瓶啤酒，nbeer的值减少一
    • $Effect(refill,\eta) = [nsoda:=max,nbeer:=max]$，表示重新填满苏打和啤酒，nsoda和nbeer的值等于最大值
  • PG图：（其中，结点内的黑色实心表示啤酒，空心表示苏打，图中初始位置只有两瓶啤酒和两瓶苏打）
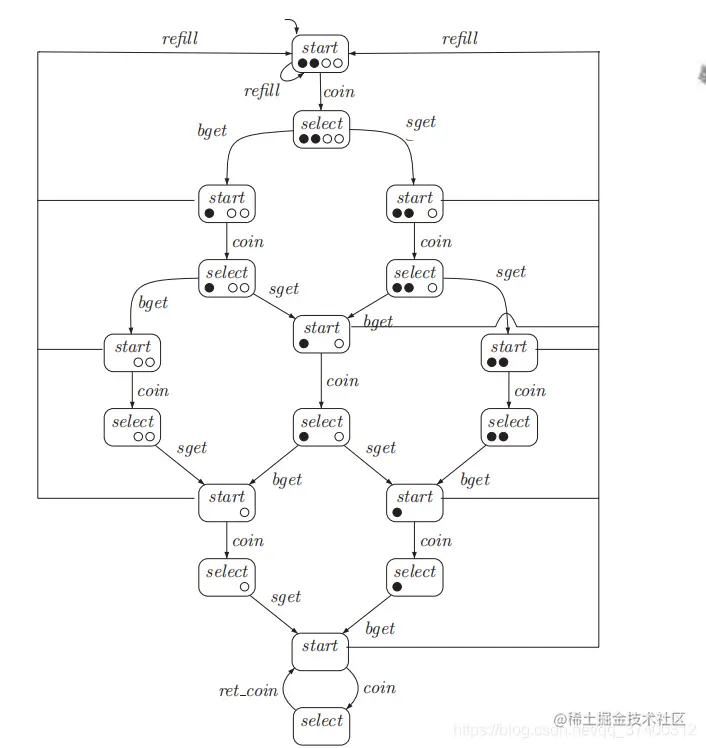
• PG转换为TS的方法
  • PG六元组： $PG = (Loc, Act, Effect, \hookrightarrow, Loc_{0}, g_{0})$ 分别是位置、动作、影响、转移关系、初始位置、初始限定条件
  • TS六元组： $TS = (S, Act,\rightarrow , I,AP, L)$ 分别是状态、动作、转移关系、初始状态、原子命题、标签函数
  • 具体转换规则如下：
    • $S=Loc \times Eval(Var)$，表示，TS的状态是位置与变量取值的笛卡尔积。具体来说，新的状态包含了位置和位置上的变量取值
    • $Act$保持不变
    • $\rightarrow \in S \times Act \times S$由以下规则定义：
  $$$$

{\ell \overset{g:\alpha }{\hookrightarrow} {\ell}' \wedge \eta \models g} {\langle \ell , \eta \rangle \overset{\alpha } {\rightarrow} \langle {\ell}' , Effect(\alpha ,\eta ) \rangle }$$ 表示，转移关系是在某状态对应于PG上的原位置$\ell$上当前赋值$\eta$满足动作$\alpha$执行条件$g$时，从原状态$\langle l,\eta \rangle$，经动作$\alpha$，到达新状态$\langle l',Effect(\alpha, \eta) \rangle$的转移关系。 其中，${\ell}'$是原PG上的位置$\ell$依动作$\alpha$经$\hookrightarrow$转移所到达的新位置（可以和$\ell$相同），而 $Effect(\alpha, \eta)$是当前的变量赋值$\eta$经$Effect$表中动作$\alpha$对应的影响操作后的新的变量赋值（可以和$\eta$相同）。

     -  $I = \{ \langle \ell , \eta \rangle \} | \ell \in Loc_{0} \cup \{ g \in Cond(Var) | \eta \models g_{0} \}$，表示初始状态是PG中的所有初始位置，和满足初始条件的所有变量赋值的笛卡尔积。
    -  $AP = Loc  \cup Cond(Var)$，表示原子命题集合是所有的位置$Loc$和PG中出现的所有条件$Cond(Var)$的并集。
     -  $L = \{ \ell \} \cup \{ g \in Cond(Var)| \eta \models g \}$，表示对状态取标签得到的是位置$\ell$以及变量赋值$\eta$所满足的限定条件$g$的集合。