关于周志华老师的《机器学习》这本书的学习笔记
记录学习过程
本博客记录Chapter12

1 基础知识

计算学习理论（computational learning theory）：关于通过“计算”来进行“学习”的理论，即关于机器学习的理论基础，其目的是分析学习任务的困难本质，为学习算法体统理论保证，并根据结果指导算法设计。

对于二分类问题，给定样本集 $\{(x_1,y_1),(x_2,y_2),\cdots,(x_m,y_m)\}$ ， $y_i\in\{-1,+1\}$ 。假设所有样本服从一个隐含未知的分布 $D$ ，所有样本均独立同分布（independent and identically distributed）。

令 $h$ 为样本到 $\{-1,+1\}$ 上的一个映射，其泛化误差为

E(h;D)=P_{x\sim D}(h(x)\neq y)

$h$ 在 $D$ 上的经验误差为

\hat{E}(h;D)=\frac{1}{m}\sum_{i=1}^m Ⅱ(h(x_i)\neq y_i)

由于D是 $D$ 的独立同分布采样，因此 $h$ 的经验误差的期望等于其泛化误差。 在上下文明确时，我们将 $E(h;D)$ 和 $\hat E(h;D)$ 分别简记为 $E(h)$ 和 $\hat E(h)$ 。令 $\epsilon$ 为 $E(h)$ 的上限，即 $E(h)\le \epsilon$ ；我们通常用 $\epsilon$ 表示预先设定的学得模型所应满足的误差要求，亦称“误差参数”。

我们将研究经验误差和泛化误差之间的逼近程度；若 $h$ 在数据集上的经验误差为0，则称 $h$ 与D一致，否则称其不一致。对于任意两个映射 $h_1,h_2\in X \rightarrow Y$ ，用不合（disagreement）来度量他们之间的差别：

d(h_1,h_2)=P_{x\sim D}(h_1(x)\neq h_2(x))

我们将会用到几个常见的不等式：

Jensen不等式：对任意凸函数，有
$f(E(X))\neq E(f(x))$
Hoeffding不等式：若 $x_1,x_2,\dots,x_m$ 为 $m$ 个独立随机变量，且满足 $0\le x_i\le 1$ ，对任意 $\epsilon>0$ ，有
$P(\frac{1}{m}\sum_{i=1}^mx_i-\frac{1}{m}\sum_{i=1}^mE(x_i)\ge\epsilon)\le e^{-2m\epsilon^2}\\ P(|\frac{1}{m}\sum_{i=1}^mx_i-\frac{1}{m}\sum_{i=1}^mE(x_i)|\ge\epsilon)\le 2e^{-2m\epsilon^2}$
McDiarmid不等式：若 $x_1,x_2,\dots,x_m$ 为 $m$ 个独立随机变量，且满足 $1\le i\le m$ ，函数 $f$ 满足：
$\sup_{x_1,\cdots,x_m,\ x_i'} |f(x_1,\cdots,x_m)-f(x_1,\cdots,x_{i-1},x_i',x_{i+1},\cdots,x_m)|\le c_i,$
则对任意 $\epsilon >0$ ，有
$P(f(x_1,\cdots,x_m)-E(f(x_1,\cdots,x_m))\ge\epsilon )\le exp (\frac{-2\epsilon^2}{\sum_ic_i^2})\\ P(|f(x_1,\cdots,x_m)-E(f(x_1,\cdots,x_m))|\ge\epsilon )\le 2\ exp (\frac{-2\epsilon^2}{\sum_ic_i^2})$

2 PAC学习

概率近似正确理论（Probably Approximately Correct，PAC）：

首先介绍两个概念：
- $C$ ：概念类。表示从样本空间到标记空间的映射，对任意样例，都能使得 $c(x)=y$ 。
- $H$ ：假设类。学习算法会把认为可能的目标概念集中起来构成 $H$ 。
- 若 $c\in H$ ，则说明假设能将所有示例按真实标记一致的方式完全分开，称为该问题对学习算法而言是”可分的“；否则，称为”不可分的“
对于训练集，我们希望学习算法学习到的模型所对应的假设 $h$ 尽可能接近目标概念 $c$ 。我们是希望以比较大的把握学得比较好的模型，也就是说，以较大的概率学得误差满足预设上限的模型，这就是"概率近似正确"的含义。形式化地说，令 $\delta$ 表示置信度，可定义:
- PAC辨识：对 $0\le \epsilon, \delta<1$ ，所有的 $c\in C$ 和分布 $D$ ，若存在学习算法，其输出假设 $h\in H$ 满足：
  $P(E(h)\le \epsilon)\ge 1- \delta$
  则称学习算法能从假设空间 $H$ 中PAC辨识概念类 $C$ 。这样的学习算法能以较大的概率(至少 $1-\delta$ ) 学得目标概念 $c$ 的近似 (误差最多为 $\epsilon$ )。在此基础上可定义:
- PAC可学习：令 $m$ 表示从分布 $D$ 中独立同分布采样得到的样例数目， $0 < \epsilon, \delta < 1$ ，对所有分布 $D$ ，若存在学习算法和多项式函数 $poly(1/\epsilon,1/delta,size(x),size(c))$ （样例数目 $m$ 与误差 $\epsilon$ 、置信度 $1-\delta$ 、数据本身的复杂度 $size(x)$ 、目标概念的复杂度 $size(c)$ 都有关），使得对于任何 $m\ge poly(1/\epsilon,1/delta,size(x),size(c))$ ，学习算法能从假设空间中PAC辨识概念类 $C$ ，则称概念类 $C$ 对假设空间而言是PAC可学习的，有时也简称概念类 $C$ 是PAC 可学习的。
- PAC学习算法：满足PAC可学习的算法。（假定学习算法处理每个样本的时间为常数，因此 $C$ 的时间复杂度等价于样本复杂度。于是，我们对算法时间复杂度的关心就转化为对样本复杂度的关心）
- 样本复杂度（Sample Complexity）：满足 $m \ge poly(1/\epsilon,1/\delta,size(x),size(c))$ 的最小的 $m$ 。
PAC学习中一个关键因素是假设空间H的复杂度。H包含了学习算法所有可能输出的假设，若在PAC学习中假设空间与概念类完全相同，即H=C，这称为"恰PAC可学习" (properly PAC learnable)。直观地看，这意味着学习算法的能力与学习任务”恰好匹配“。然而，这种让所有候选假设都来自概念类的要求看似合理，但却并不实际，因为在现实应用中我们对概念类 $C$ 通常一无所知，更别说获得一个假设空间与概念类恰好相同的学习算法。显然，更重要的是研究假设空间与概念类不同的情形，即 $H\neq C$ 。一般而言， $H$ 越大，其包含任意目标概念的可能性越大，但从中找到某个具体目标概念的难度也越大。 $|H|$ 有限时，我们称究为"有限假设空间"，否则称为"无限假设空间"。

3 有限假设空间

3.1 可分情形

对于PAC来说，只要训练集 $D$ 的规模能使得学习算法以概率 $1-\delta$ 找到目标假设的 $\epsilon$ 近似即可。

先估计泛化误差大于 $\epsilon$ 但在训练集上仍表现完美的假设出现的概率。假定 $h$ 的泛化误差大于 $\epsilon$ ，对分布 $D$ 上随机采样而得到的任何样例 $(x,y)$ ，有：

P(h(x)=y)=1-P(h(x)\neq y)\\ \ \ \ \ \ \ \ \ \ \ =1-E(h)\\ \ \ \ \le1-\epsilon

由于 $D$ 中包含 $m$ 个样例，因此， $h$ 与 $D$ 表现一致的概率为：

P((h(x_1)=y_1)(h(x_2)=y_2)\cdots(h(x_m)=y_m))<(1-\epsilon)^m

我们事先不知道学习算法会输出那个假设，但仅需要保证泛化误差大于 $\epsilon$ ，且在训练集上变现完美的多有假设出现概率之和不大于 $\delta$ 即可。

P(h\in H:E(h)>\epsilon \ \cap \ \hat E(h)=0) \lt |H|(1-\epsilon)^m\\ \lt |H|e^{-m\epsilon}

令上式不大于 $\delta$

|H|e^{-m\epsilon}\le \delta

可得

m \ge \frac{1}{\epsilon}(\ln|H|+\ln \frac{1}{\delta})

由此可知，有限假设空间 $H$ 都是PAC可学习的，所需的样例数目如上式所示，输出假设 $h$ 的泛化误差随样例数目的增多而收敛到 0，收敛速率为 $O(\frac{1}{m})$ 。

3.2 不可分情形

当 $c\notin H$ 时，我们的学习算法无法学习到目标概念 $c$ 的 $\epsilon$ 近似，但是当假设空间给定时，必定存在一个泛化误差最小的假设，找出此假设的 $\epsilon$ 近似也不失为一种较好的目标。

$H$ 中泛化误差最小的假设是 $\arg \min_{h\in H} E(h)$ ，以此为目标可将PAC学习推广到 $c\notin H$ 的情况，称为**”不可知学习“**（agnostic learning）。其概念如下：

令 $m$ 表示从分布 $D$ 中独立同分布采样得到的样例数目， $0\lt \epsilon,\delta \lt 1$ ，对所有分布 $D$ ，若存在学习算法和多项式函数 $poly$ ，使得对于任何 $m\ge poly(1/\epsilon,1/\delta,size(x),size(c))$ ，学习算法能从假设空间中输出满足下式的假设 $h$ ：

P(E(h)-\min_{h'\in H}E(h')\le \epsilon)\ge1-\delta

则称假设空间是不可知PAC学习的。

4 VC维

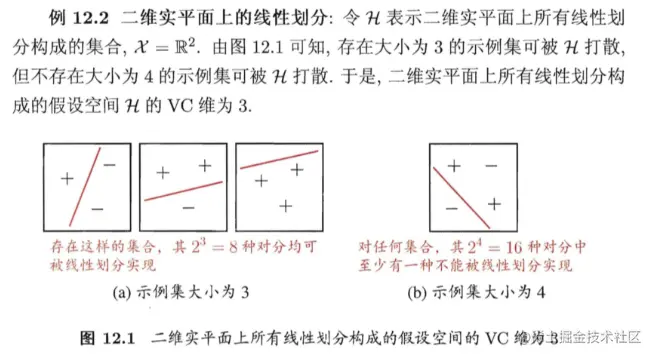
VC维：假设空间 $H$ 的VC维是能被 $H$ 打散的最大示例集的大小：

VC(H)=\max \{m:\Pi_{H}(m)=2^m \}

例如对二分类问题来说，m个样本最多有 $2^m$ 个可能结果，每种可能结果称为一种“对分”，若假设空间能实现数据集D的所有对分，则称数据集能被该假设空间打散。VC维指能被 $H$ 打散的最大示例集的大小。

应注意到，VC维与数据分布 $D$ 无关！在数据分布未知时，仍能计算出假设空间的VC维。

若假设空间 $H$ 的VC维是 $d$ ，则对任意整数 $m \gt d$ ，有：

\Pi_H (m)\le (\frac{e\cdot m}{d})^d

同时任何VC维有限的假设空间 $H$ 都是（不可知）PAC学习的。

5 Rademacher复杂度

Rademacher 复杂度 (Rademacher complexity) 是另一种刻画假设空间复杂度的途径，与VC维不同的是，它在一定程度上考虑了数据分布。

考虑实值函数空间 $F \rightarrow \mathbb R$ ，令 $Z=\{z_1,z_2,\cdots,z_m\}$ 。函数空间 $F$ 关于 $Z$ 的经验Rademacher复杂度

\hat R_Z(F)=\mathbb E_{\sigma}[ \sup_{f\in F}\frac{1}{m}\sum_{i=1}^m\sigma_if(z_i) ]

经验Rademacher复杂度衡量了函数空间 $F$ 与随机噪声在集合 $Z$ 中的相关性。通常我们希望了解函数空间 $F$ 在 $Z$ 上关于分布 $D$ 的相关性，因此，对所有从 $D$ 独立同分布采样而得的大小为 $m$ 的集合 $Z$ 求期望可得

R_m(F)=\mathbb E_{Z \subseteq Z:|Z|=m}[\hat R_Z(F)]

假设空间 $H$ 的Rdemacher复杂度 $R_m(H)$ 与增长函数 $\Pi_H(m)$ 满足

R_m(H)\le \sqrt{\frac{2\ln \Pi_H(m)}{m}}

6 稳定性

顾名思义，算法的“稳定性”考察的是算法在输入发生变化时，其输出是否会随之发生较大的变化。学习算法的输入是训练集，因此下面我们先定义训练集的两种变化：

移除： $D^{\backslash i}$ ，表示移除 $D$ 中第 $i$ 个样例得到的集合
$D^{\backslash i}=\{z_1,z_2,\cdots,z_{i-1},z_{i+1},\cdots,z_m \}$
替换： $D^{i}$ ，表示替换 $D$ 中第 $i$ 个样本得到的集合
$D^i=\{z_1,z_2,\cdots,z_i',\cdots,z_m \}$

损失函数刻画了预测标记和真实标记的差别：

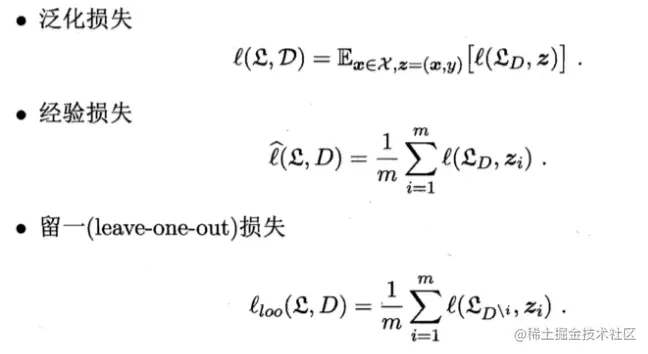
算法的均匀稳定性：

因此，移除示例的稳定性包含了替换示例的稳定性。

若学习算法符合经验风险最小化原则（ERM）且稳定的，则假设空间 $H$ 是可学习的。稳定性通过损失函数与假设空间的可学习联系在了一起。

机器学习 第十二章计算学习理论