209. 长度最小的子数组
描述:
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
示例:
-
示例 1:
输入:target = 7, nums = [2,3,1,2,4,3] 输出:2 解释:子数组 [4,3] 是该条件下的长度最小的子数组。
-
示例 2:
输入:target = 4, nums = [1,4,4] 输出:1
-
示例 3:
输入:target = 11, nums = [1,1,1,1,1,1,1,1] 输出:0
思路:
-
最简单的就是暴力法, 通过遍历数组, 以每一个数组的索引值作为初始值, 再次遍历, 获取符合条件的子数组长度, 将最小值返回.
LeetCode官方的解释说的清楚一些, 直接贴: 初始化子数组的最小长度为无穷大,枚举数组 \text{nums}nums 中的每个下标作为子数组的开始下标,对于每个开始下标 ii,需要找到大于或等于 ii 的最小下标 jj,使得从 \text{nums}[i]nums[i] 到 \text{nums}[j]nums[j] 的元素和大于或等于 ss,并更新子数组的最小长度(此时子数组的长度是 j-i+1j−i+1)
-
暴力法的时间复杂度是O(n^2^), 这个复杂度让人很不满意, 使用双指针法, 可以将时间复杂度降到O(n).
-
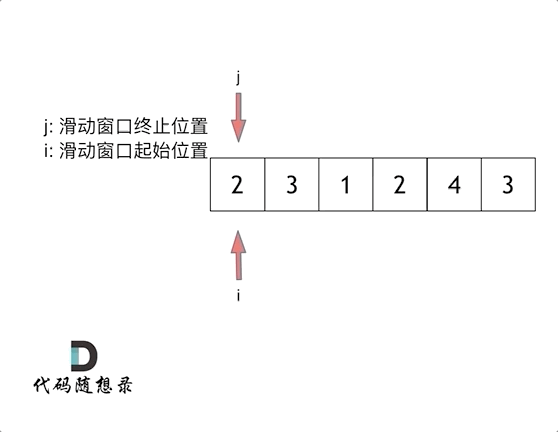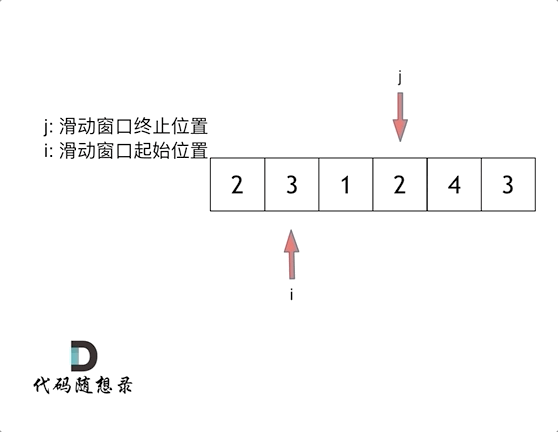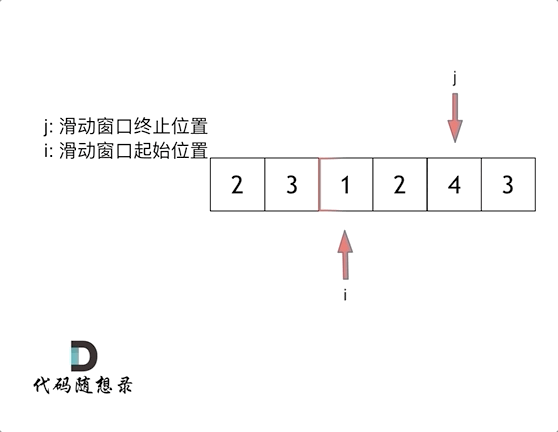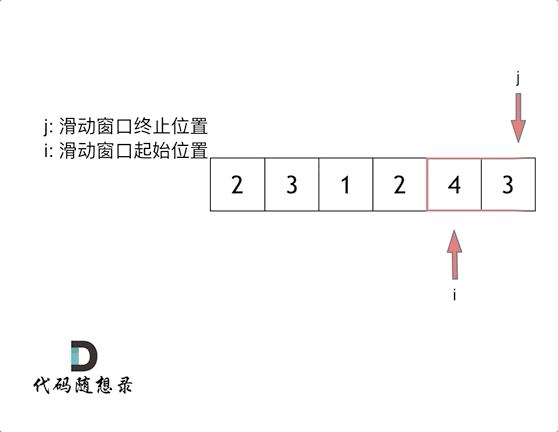
这里也使用到了两个索引作为指针, 具体的操作比较像窗口的滑动, 所以在这里这个方法被称为滑动窗口法
-
这里的滑动窗口法, 通过不断地调解子序列的起始位置和终止位置, 从而得出想要的结果.
代码:
/*
* @lc app=leetcode.cn id=209 lang=cpp
*
* [209] 长度最小的子数组
*/
// @lc code=start
class Solution
{
public:
int minSubArrayLen(int target, vector<int> &nums)
{
int result = __INT32_MAX__;
int sum{0};
int i{0};
int length{0};
for (int j = 0; j < nums.size(); j++)
{
sum += nums[j];
while (sum >= target)
{
length = j - i + 1;
result = result < length ? result : length;
sum -= nums[i++];
}
}
return result == __INT32_MAX__ ? 0 : result;
}
};
复杂度分析
时间复杂度:O(n),其中 nn 是数组的长度。指针start 和end 最多各移动 n 次。
空间复杂度:O(1)