本文已参与「新人创作礼」活动,一起开启掘金创作之路。
项目到模型的转换原因
当我们需要对一个项目进行验证时,我们无法对该项目直接验证,而是要转换成可以做验证的模型,比如一个C语言程序,要先将它转换为一阶逻辑公式,再将一阶逻辑公式转换为Kripke结构,之后我们才能进行验证分析,得到我们所需的结论。
本章基本词汇解释
-
State(状态):系统在某一时刻的特性,也值程序中所有变量的值。例如:交通灯的红色、黄色、绿色。
-
Transition(转换/转移/迁移):指从一个状态到另一个状态的演化。例如:交通灯由红色变为黄色。
在程序中,可以理解为
- 当前时刻:{x=1,y=2}
- 执行变迁:x=5,y=x+1
- 下一时刻:{x=5,y=6}
-
Action(动作):过程之间的沟通机制。
-
Atomic Propositions(原子命题):形式化临时特征。原子表示不可再分,命题表示这是具有判断能力的陈述句。例如:X=1;店里没有顾客。
-
Kripke Structure(状态迁移系统):是一个基于原子命题AP的四元组,用M表示,M=(S,S0,R,L)
- S是有限状态集合
- S0是初始状态集合
- R是状态之间的关系,如R⊆S×S,表示状态之间所有的关系。(这里的×表示笛卡尔积)
- L是一个标签函数,状态到原子命题集合的一个函数,如L(s0)={a,b}
-
First order logic(一阶逻辑系统):用一阶逻辑描述并发系统的状态,有四个属性:
- V={v1,⋯,v1}表示系统变量集合
- D表示变量的有限域,比如布尔值变量的有限域为{true,false}
- A表示变量V到有限域D的一个映射(也叫赋值)
- state:使它为真的公式就是状态。比如S=(v1=2)∧(v2=3),因为v1=2和v2=3都为真,所以(v1=2)∧(v2=3)也为真,因此S称之为状态。
- 如果D={2,3,4,5},S={(v1=2)∧(v2=3)∧(v3=5)},则该S其实表示了三个状态:
- S1={(v1=2)∧(v2=3)∧(v3=2)}
- S2={(v1=2)∧(v2=3)∧(v3=3)}
- S3={(v1=2)∧(v2=3)∧(v3=4)}
- 状态之间的合并用∪表示,如S1∪S2∪S3
- 并发系统以一阶逻辑系统公式进行转换的过程:
- V表示当前的变量集合,V′表示下一时刻变量的集合,如V={v1,v2,v3},V′={v1′,v2′,v3′},v1←2,v2←3,v3←5,v1′←1,v2′←5,v3′←4
- 转移过程:(v1=2∧v2=3∧v3=5)∧(v1′=1∧v2′=5∧v3′=4)
-
Transition System(转换系统,简称TS):是一个六元组,TS=(S,Act,→,I,AP,L)
- Act是组动作的合集;
- →表示转换关系,→⊆S∗Act∗S,是状态-动作-状态的转移关系集合;
- I是一组初始状态,I⊇S;
- AP是一组原子命题;
- L是一个标签函数,S→2AP;
如果状态集S、动作集Act、原子命题AP都是有限的,那么称这个TS是有限的。
基本动作的转移公式:S→αS′
- 含义: 动作α将状态S转变为状态S′。
- 备注:
- S的下一个状态S′是不确定的,只有经历了动作α的转换,S的下一个状态S′才被确定下来;
- 当初始状态集包含超过1个状态时,初始状态S也是非确定的;
- 动作是为通信建模而引入的机制,其它操作无需在意动作所执行的内容。
标签函数(Label function):L(s)∈2AP
- 状态s满足命题逻辑公式Φ如果L(s)使公式Φ真;即s⊨Φ iff L(s)⊨Φ;
- 原子命题集合AP应当选择感兴趣的特征,也就是模型需要考虑的特征;
- 用法举例:L(select) = { paid },表示在select状态时,取得的标签为paid。
- L(s)∈2AP其实就是L(s)⊆AP,原子性质集合
构建Kripke Sructure模型
需要根据程序的四个特征进行建模:顺序、分支、循环、并发
顺序程序(Sequential program)的建模
- 方法:对程序进行标签化
- 目的:将程序一条条处理
- 打标签的四个方法:
- 如果是一条普通的语句P,则标签为:PL=P
- 如果是两条语句P=P1;P2,则标签为:PL=P1L;l′′:P2L
- 如果是分支语句P=if b then P1 else P2 endif,则标签为:PL=if b then l1:P1L else l2:P2L endif
- 如果是循环语句P=while b do P1 endwhile,则标签为:PL=while b do l1:P1L endwhile
- 程序初始状态集合:S0(V,pc)≡pre(V)∧pc=m
- pre(V)表示V的初始值,pc表示当前的语句入口,pc′表示当前的语句出口,仅限于该条语句,而m表示程序的入口,m′表示程序的出口,作用于整个程序(在后面的练习中可以深刻体会他们的区别)
- ≡表示左右两侧的公式等价,所代表的含义相同,只不过表达方法不同而已
-
翻译过程:C(l,P,l′)表示程序入口为l,出口为l′,程序要执行的语句为P,C表示这是一个要翻译的过程,翻译过程一般会有如下五种语句被翻译:
- 赋值语句:C(l,v←e,l′)≡pc=l∧pc′=l′∧v′=e∧same(V\{v})
- 空语句:C(l,skip,l′)≡pc=l∧pc′=l′∧same(V)
skip表示什么也不执行,空语句存在的目的是为了程序中对其语句等作用
-
顺序语句:C(l,P1;l′′:P2,l′)≡C(l,P,l′)∨C(l,P2,l′)
-
条件语句:
C(l,if b thenl1:P1 else l2:P2 endif,l′)≡(pc=l∧pc′=l1∧b∧same(V))∨(pc=l∧pc′=l2∧¬b∧same(V))∨C(l1,P1,l′)∨C(l2,P2,l′)
-
循环语句:
C(l,while b do l1:P1 endwhile,l′)≡pc=l∧pc′=l1∧b∧same(V))∨pc=l∧pc′=l1∧¬b∧same(V))∨C(l1,P1,l)
- same(V)表示V中变量不发生变化
- same(V\{v})表示V中变量只有v发生变化
- 有些地方用l′,l′′有些地方用l1,l2的原因,个人感觉,应该是顺序语句用l′,l′′,分支循环这种很多可能性的用l1,l2
-
练习题:对如下程序进行标签化
V={x,y,z},initial value:x=y=z=0Program:x=y+1;z=z+2;for(y;y<=3;y++)if x<y then x++;else y++;
-
答案(答案不唯一):
- 初始化程序,先将程序标记分为三个标记语句
P1:x=y+1;z=z+2;P2:for(y;y<=3;y++)P3:if x<y then x++;else y++;
- 对P1继续标记:
P11:x=y+1P12:z=z+2P1L=P11L;l12=P12LP11L=P11P12L=P12
- 对P2继续标记:
首先将for语句转变为while语句
ywhile(y<=3)doP3y++endwhile
然后进行标记
P21:yP22:y++P2L=P21L;l23′′=P23LP21L=P21P22L=P22P23L=while(y<=3)dol3:P3L;l22:P22L endwhile
- 再对P3进行标记:
P31:x++P32:y++P3L:if x<y then l31:P31L elsel32:P32L endifP31L=P31P32L=P32
- 由上述标记公式,可得一阶逻辑公式:
- x=0∧y=0∧z=0∧pc=m∧pc′=l11
- x′=y+1∧same(V\{x})∧pc=l11∧pc′=l12
- z′=z+2∧same(V\{z})∧pc=l12∧pc′=l2
- y<=3∧same(V)∧pc=l2∧pc′=l21
- ¬(y<=3)∧same(V)∧pc=l2∧pc′=l22
- same(V)∧pc=l21∧pc′=l3
- same(V)∧pc=l22∧pc′=m′
- x<y∧same(V)∧pc=l3∧pc′=l31
- ¬(x<y)∧same(V)∧pc=l3∧pc′=l23
- x′=x+1∧same(V\{x})∧pc=l31∧pc′=l23
- y′=y+1∧same(V\{y})∧pc=l31∧pc′=l23
- y′=y+1∧same(V\{y})∧pc=l23∧pc′=l2
IMP语言转一阶逻辑公式再转Kripke Structure程序
- IMP语法规则:
- Aexp:a::=n∣x∣a0+a1∣a0−a1∣a0×a1,n∈[0,2]
- Bexp:b::=true∣false∣a0==a1∣a0≤a1∣¬b∣b0∧b1∣b0∨b1
- Com:
c::=cobegin p1∣∣p2 coendp::=skip;∣x:=a;∣p0;p1∣wait(b)∣if b then p0 else p1∣while b do p
- 整形变量取值范围:[0,1,2]
- 布尔变量取值范围:[0,1]
- 变量名规则:单个小写字母,如a,b,c,⋯
- 样例1:
- 输入IMP语言:
x:=1;y:=1;x:=x+y;
- 输出一阶逻辑公式:
D≡{0,1,2}V≡{x,y}S0(x,y)≡x=1∧y=1
R≡x=1∧y=1∧pc=m∧pc′=l1x′=x+y∧same(V\{x})∧pc=l1∧pc′=m′
- 输出Kripke Structure:
KS=(S,S0,R,L)
S={<1,1>,<2,1>}
S0={<1,1>}
R(x,y,x′,y′)≡x′=(x+y)mod 3∧y′=y
L(S0)={1,1}
L(S1)={2,1}
- 输出Kripke Structure图形形式:
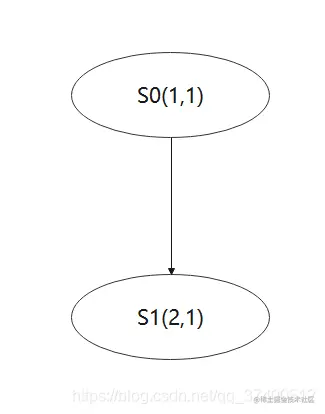
- 样例2:
某大佬程序里直接跑的结果:
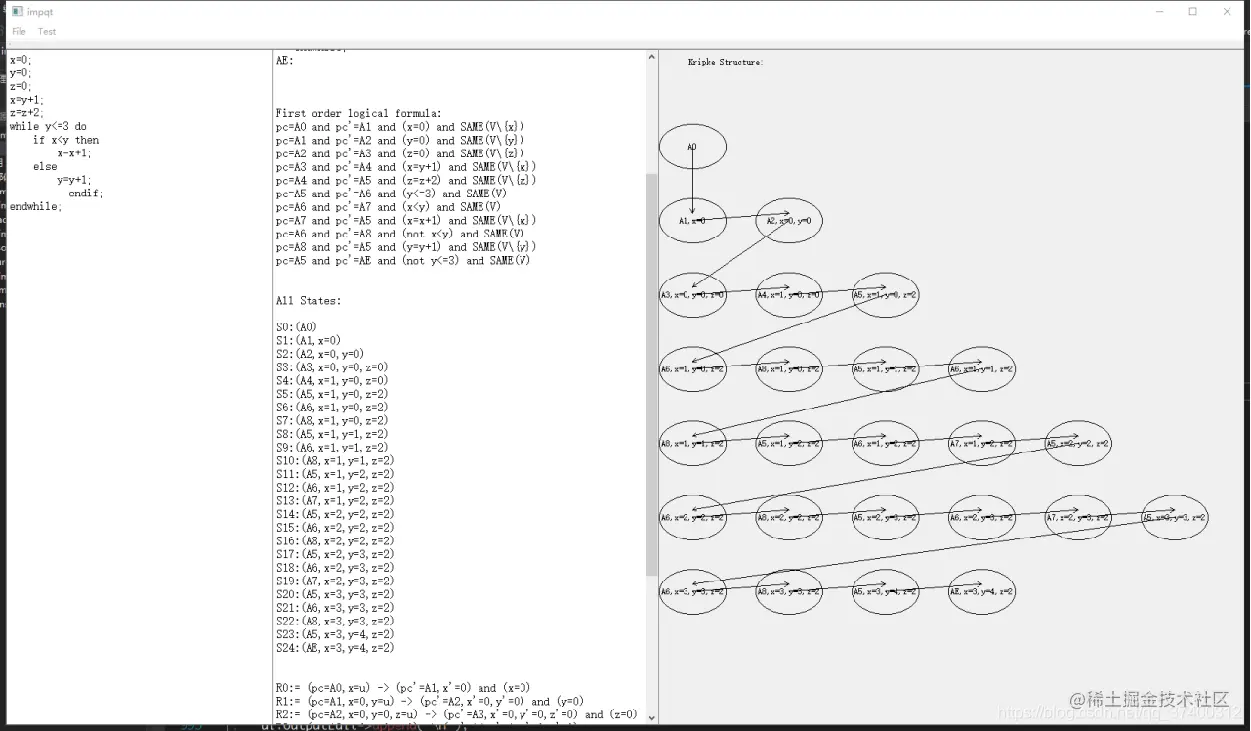

- 答案:
一个大佬用python写的程序:github.com/lypnol/impy
另一位大佬C++写的程序:git.code.tencent.com/fasasas/for…
- 如果你是华师大郭老师的课程,这两个程序只能参考,千万别照搬,这俩郭老师都看过了,不要抱侥幸心理哦
- 输入输出格式不唯一
并发程序(Concurrent programs)的建模
-
原因:由一组同时执行的进程组成,进程是顺序语句,我们假设CPU是单核的,所以程序只能异步执行,一次只能执行一条语句,所以我们要进行并发建模
-
组成:
V:并发进程变量的集合
pci:第i个并发进程
pc:并发进程的计数器
PC:并发进程的计数器的集合
-
表示方法:P=Cobegin P1∣∣P2∣∣⋯∣∣Pn coend
-
标记并发程序:PL=conbegin l1:P1L l1′∣∣l2:P2L l2′∣∣⋯∣∣ln:PnL ln coend
-
并发程序初始状态:S0(V,pc)≡pre(V)∧pc=m∧i=1∧n(pci=⊥)
-
并发程序执行过程:
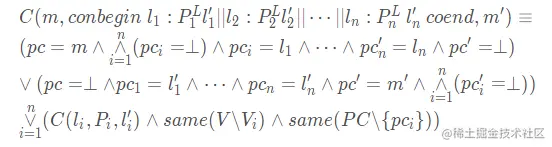
- ⊥表示数值为空或否,pc=⊥表示程序未被激活
- i=1∧n(pci=⊥))表示pc1=⊥∧pc2=⊥∧⋯∧pcn=⊥
-
共享变量
- 原因:当一个变量被一个进程访问时,其他变量如果想访问,需要将此变量共享才可以
- 方法:
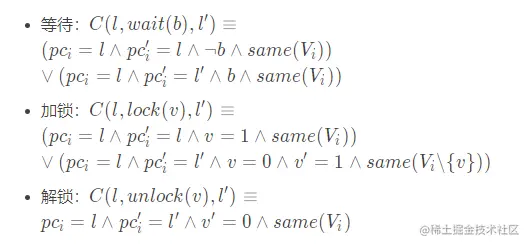
-
P初始状态:S0(V,pc)≡pc=m∧pc0=⊥∧pc1=⊥∧(turn=0∨turn=1)
-
P的转移关系
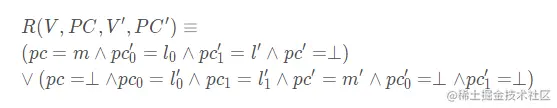
并发还有没整理完,太多了,太难理解,以后有机会再整理
可满足性关系(Satisfaction relation):⊨
- 举个简单的例子:μ⊨ a>0 if a=1,表示当a=1的时候,a>0的结果为true,最终μ⊨true,可满足性关系的式子成立。换句话说,就是当且仅当a=1时,μ满足a>0(也就是μ⊨true)。
- true。此时μ⊨true也就是μ⊨后面的这个结果为true或,才表示可满足性关系。
- 专业解释:对原子命题集合AP的定值是将其映射到0或1上,即 μ:AP→{0,1},记Eval(AP)是AP内命题的全部的真值指派方式组成的集合。可满足关系⊨是一个二元关系(μ,ϕ),它指示的是在μ这个定值方式下,命题逻辑公式ϕ的计算结果为真。
- 真值指派:此处可以理解成对变量的赋值影响相关原子命题的真值,例如设置a=2那么命题a>0的真值为真,将所有的命题计算得到的真假,即是对整个合取式的真值指派。
- 如果上面的文字还没能理解,那么我们再多举几个例子
- μ⊨true
- μ⊨aiffμ(a)=1
- μ⊨ϕ1∧ϕ2iffμ⊨ϕ1andμ⊨ϕ2
非确定性的应用(Application of nondeterministic)
- 通过两进程交替执行对独立活动的并行执行进行建模;
- 对两个进程访问同一共享资源而出现的复杂状况建模;
- 用于抽象的目的或者不规范的场景;
- 对未知或不可预测环境下的接口建模。
- 例题:
- 向自动售货机内插入硬币后,可以选择购买啤酒或苏打水
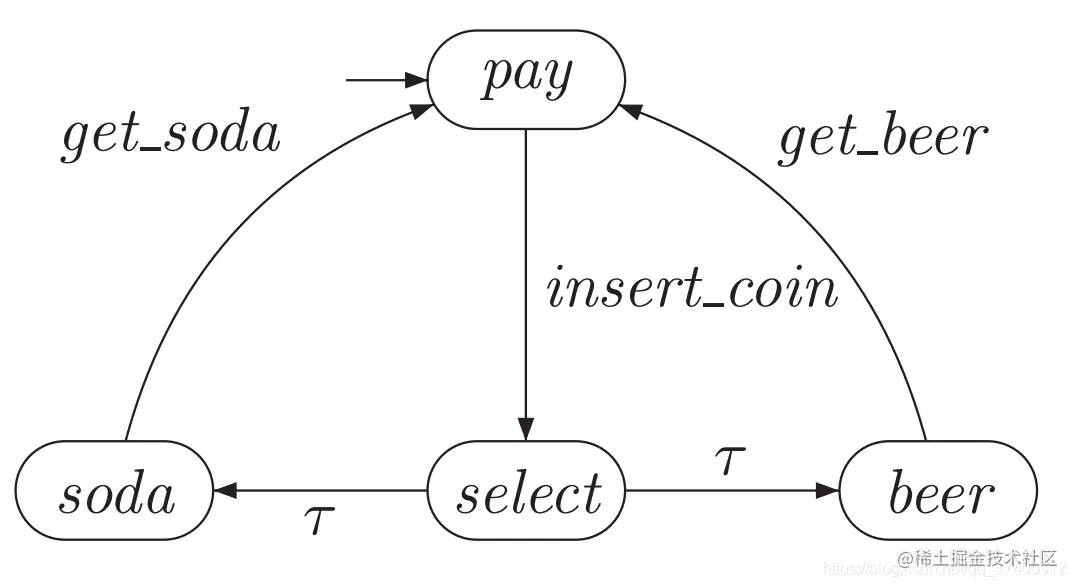
- S = { pay , select, soda, beer }
- I = { pay }
- Act = { insert_coin, get_soda, get_beer, τ }
- 问题:请给出AP和L
答案:
AP = { paid , drink }
L(pay) = $\varnothing$
L(soda) = L(beer) = { paid , drink }
L(select) = { paid }
- 答案解析:paid表示投入了硬币,drink表示饮料取出喝掉,这两个状态的取值只能为真或假。一开始既没有付款也没有喝饮料,所以对pay取标签函数得到的是空集;在投入硬币进入select状态后,因为已经付款了,所以取标签得到的是{paid};在出了饮料之后,即认为同时也可以喝了,所以取标签得到的是{paid,drink}。
- 这是一个非确定的系统,因为在投入硬币后,既可以选择提供啤酒,也可以选择提供苏打水。
- 当表示内部活动或者不相关活动时,使用一个特殊符号τ
- Act 用于建模和数据通信
- AP的集合总是根据题目所需的特征来选择
从一阶逻辑公式构造Kripke structure(KS)例题
- 题目:
- V={x,y}
- D={0,1}
- S0=(x,y)≡x=1∧y=1
- Transition:
R(x,y,x′,y′)≡x′=(x+y) mod 2 ∧y′=y
- 问题:
- KS=(S,S0,R,L)
- 解析:
- 该系统的所有状态用<x,y>有序对来表示,而x和y的值域均为D={0,1},所以<x,y>的所有取值就是D和D的笛卡尔积来计算,S=D×D={<0,0>,<0,1>,<1,0>,<1,1>}
- 按照描述,系统的初始状态集合为S0(x,y)≡x=1∧y=1,所以初始状态S0={<1,1>}
- 我们需要从系统的每一个状态开始,分别计算经过转移后系统所达到的新状态。首先计算x=0,y=0的情况,一次转移后,即计算新的x和y值,得到<(0+0) mod 2,0>,计算mod后结果为<0,0>,依次计算其余状态,我们可以得到<1,0>→<1,0>,<1,1>→<0,1>,<0,1>→<1,1>,将其用KS的形式表示为R={(<0,0>,<0,0>),(<1,0>,<1,0>),(<0,1>,<1,1>),(<1,1>,<0,1>)}
- 标签函数代表着某状态下取值为真的原子命题,即L(<1,1>)={x=1,y=1},L(<0,1>)={x=0,y=1},L(<0,0>)={x=0,y=0},L(<1,0>)={x=1,y=0}
- ≡表示等同于,意思是执行S0(x,y)与执行x=1∧y=1的作用相同
- ∧表示左右两个式子同步执行,∨表示左右两个式子依次执行
- S0=(x,y)≡x=1∧y=1表示初始状态下,x的值为1,y的值也为1
- R(x,y,x′,y′)≡x′=(x+y) mod 2 ∧y′=y表示转移关系,x′的值为(x+y) mod 2,y′的值仍然为y
-
图像表示为:
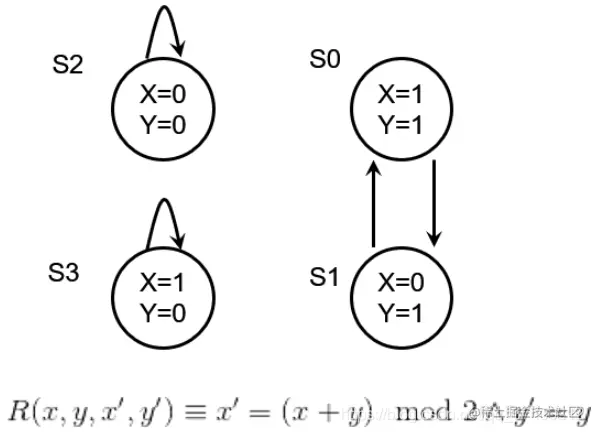
-
答案:
- S={{x=1∧y=1},{x=0∧y=1}}
- S0={{x=1∧y=1}}
- R={{x=1∧y=1∧x′=0∧y′=1},{x=0∧y=1∧x′=1∧y′=1}}
- L(S0)={x=1∧y=1}
- L(S1)={x=0∧y=1}
直接前驱和直接后继(Direct Predecessors and Successors expanded)
对于转换状态TS=(S,Act,→,I,AP,L),如果s∈S且α∈Act
-
一组α的直接前驱定义为:
Pre(s,α)={s′∈S∣s′→αs}
Pre(s)=⋃α∈ActPre(s,α)
-
一组α的直接后继定义为:
Post(s,α)={s′∈S∣s→αs′}
Post(s)=⋃α∈ActPost(s,α)
-
直接前驱和直接后继者扩展到子集:
Post(C,α)=⋃s∈CPost(s,α)
Post(C)=⋃s∈CPost(s)
Pre(C,α)=⋃s∈CPre(s,α)
Pre(C)=⋃s∈CPre(s)
-
转换状态TS的终止状态:
Post(C)=∅
对于顺序计算机程序,终止状态表示程序的终;对于并行系统,终止状态通常被认为是不理想的。
确定性的转换系统(Deterministic Transition System)
- 关于action的确定转换系统
- 对所有状态s和动作α ,都有
∣I∣⩽1 and ∣Post(s,α)∣⩽1
- 表示任意状态经任意动作最多跳转到1个状态去
- 这种系统叫做行动决定(action-deterministic)
- 关于AP的确定转换系统
- 对所有状态s和AP的子集A∈2AP,都有
∣I∣⩽1 and ∣Post(s)∩{s′∈S∣L(s′)=A}⩽∣1
- 表示从某一状态出发的直接后继,其Label函数的计算结果一定是不一样的
- 这种系统叫做AP决定(AP-deterministic)
执行片段(Execution fragment)
- 对于转换状态TS=(S,Act,→,I,AP,L),有两种执行片段
- 有限执行片段
- 公式:ρ=s0α1s1α2...αnsn, 其中:对于所有的0⩽i⩽n,都有si→αi+1si+1
- 公式含义:初始状态s0,执行α1后,状态变为s1,执行α2后,状态变为s2……状态变为sn−1,执行αn后,状态变为sn
- 无限执行片段
- 公式:ρ=s0α1s1α2..., 其中:对于所有的0⩽i,都有si→αi+1si+1
- 公式含义:初始状态s0,执行α1后,状态变为s1,执行α2后,状态变为s2……$
n表示有限片段的长度,n的值大于等于0
- 初始执行片段: 最大执行片段要么是以终止状态结束的有限执行片段,要么是无限执行片段。
- 最大执行片段:如果执行片段以初始状态启动,则称为初始片段。
- 执行状态:一个初始的、最大的执行片段。
- 可达状态:一个初始的、有限的执行片段。