张志华 统计机器学习_Leibniz infinity sml的博客-CSDN博客

统计机器学习-张志华-例子-Bayesian Linear Models

Bayesian Linear Models

问题描述:

$y_i={x_i}^{T} b + \epsilon_i$

$y_i \in \R$

${x_i}^{T} \in \R^p$

$D=\{(x_1,y_1), (x_2,y_2), ... ,(x_i,y_i), ... ,(x_n,y_n)\}$

假定:$\epsilon_i \sim \mathcal{N}(0,\sigma^2)$

这里实际上描述了 $p(D|b,\sigma^2)$是个高斯分布 即: $p(D|b,\sigma^2) = \prod_{i=1}^{n} p(\epsilon_i|b,\sigma^2)$

---

$p(b,\sigma^2)=p(b|\sigma^2)p(\sigma^2)$

给分布:

$p(b|\sigma^2) = \mathcal{N}(m,\sigma^2 v)$

$p(\sigma^2)=InverseGamma(a,b)$

---

演算:

$p(b,\sigma^2)=\frac{ b^a \sigma^{2(-a+\frac p 2 + 1)} } { (2\pi)^{\frac p2 } |v|^{\frac 1 2} \Gamma(a)} e^{-((b-m)^T v^{-1} (b-m) + 2b)/2v^2}$

---

$p(D|b,\sigma^2)$

---

应该让$p(b,\sigma^2|D)$和$p(b|\sigma^2)$有相同的形式，即共轭：

$p(b,\sigma^2|D)= \mathcal{N}(\hat{m},\hat{v}) InverseGamma(\hat{a},\hat{b})$ 　　　　　　　 ($p(b,\sigma^2|D)$的共轭样子式)

---

$p(b,\sigma^2|D)$ 是 Gibbs采样中 提到的 $f(b,\sigma^2)$

---

$p(b,\sigma^2|D)=\frac{p(D|b,\sigma^2) p(b,\sigma^2)}{p(D)}$

演算:

$p(b,\sigma^2|D) \propto p(D|b,\sigma^2) p(b,\sigma^2)$

$p(b,\sigma^2|D) \propto \big( \prod_{i=1}^{n} p(\epsilon_i|b,\sigma^2) \big) p(b,\sigma^2)$ ，把右边凑成 "$p(b,\sigma^2|D)$的共轭样子式" 的样子

之后　开始抽样(比如用gibbs采样)：

给定$\sigma^2$， 从$f(b|\sigma^2)$中抽b

给定b ， 从$f(\sigma^2|b)$中抽$\sigma^2$

---

遗留问题： 超参数 比如 a、b 应该设置成多少? （?初始化?应该设置成多少?)

说是有些papaer中有说

---

有说一篇paper , 没听明白名字 : ?rjx? 单元 多元 高斯问题?

统计机器学习-张志华-例子-Bayesian Classsification

$y_i \in \{0,1\}$　　　 　　　 (y的下标i是我自己加的)

$p(y_i|b)={(\mu_i(b))}^y {(1-\mu_i(b))}^{(1-y)}$　　：　Bernoulli Distribution (伯努利分布) (y的下标i是我自己加的) （$p(y_i|b)$式子）

$\mu_i(b)=h({x_i}^T b)$　　　　

$p(D|b)=\prod_{i=1}^{n} p(y_i|b)$　　　 　　　 带入"$p(y_i|b)$式子"，得：

$p(D|b)=\prod_{i=1}^{n} \big( {(\mu_i(b))}^y {(1-\mu_i(b))}^{(1-y)} \big)$ 　　　 　　　 "$p(D|b)$式子"

$(x_i,y_i)$是一个样本, 共n个样本 　　 　　　 (这句话是我自己加的)

---

h函数说明:

h函数的作用是将输入映射到区间[0,1]之间，因为上式伯努利分布中的$\mu(b)$需要是在区间[0,1]之间。

h通常有以下两种：

$h(\eta)=\frac{e^{\eta}} {1+e^{\eta}}$　　　即sigmoid函数

$h(\eta)=\Phi(\eta)=\int_{-\infty}^{\eta} \frac{1}{\sqrt{2\pi}} e^{-\frac{t^2}{2}} dt$ 　　　积分里的式子是标准高斯分布的cdf

---

临时插的话:

?probit model? 说的是 $\Phi(\eta)$?

---

继续

$b \sim \mathcal{N}(m,v)$

---

概率图

---

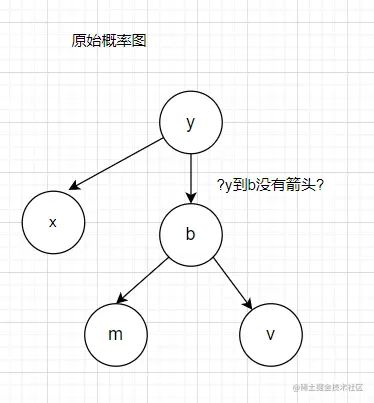
直接带入得不到共轭形式： (所以需要 用auxiliary variable method)

$p(b|D)=\frac{p(D|b) p(b)}{p(D)}$　　　 　　　 去掉?常数项$p(D)$?，得：

$p(b|D) \propto p(D|b) p(b)$ 　　，带入 "$p(D|b)$式子"得：

$p(b|D) \propto \bigg( \prod_{i=1}^{n} \big( {(\mu_i(b))}^y {(1-\mu_i(b))}^{(1-y)} \big) \bigg) p(b)$ 　　 　　　注意，这个式子由于 "y在指数中: ${*}^y$， ${*}^{1-y}$ " 导致这个式子不可能和 "p(b):高斯分布" 的形式一致， 即这个式子不会和"p(b):高斯分布"共轭，因此不能这么写（得想其他办法）

("? 还是由于b的指数是y? ")

---

(题外话)data augmentation (DA) (数据增强) : 实质是 ?增加中间变量? , 比如以下方法:

auxiliary variable method (辅助变量法)

EM算法 (expectation maximization algorithm)

latent (隐变量)

---

auxiliary variable method (辅助变量法)

增加变量z

---

引入变量z后的概率图

---

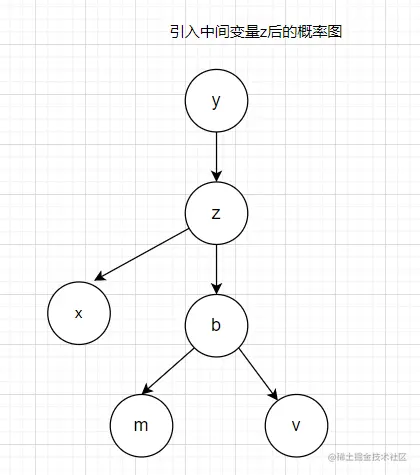
引入中间变量z前后的概率图对比

---

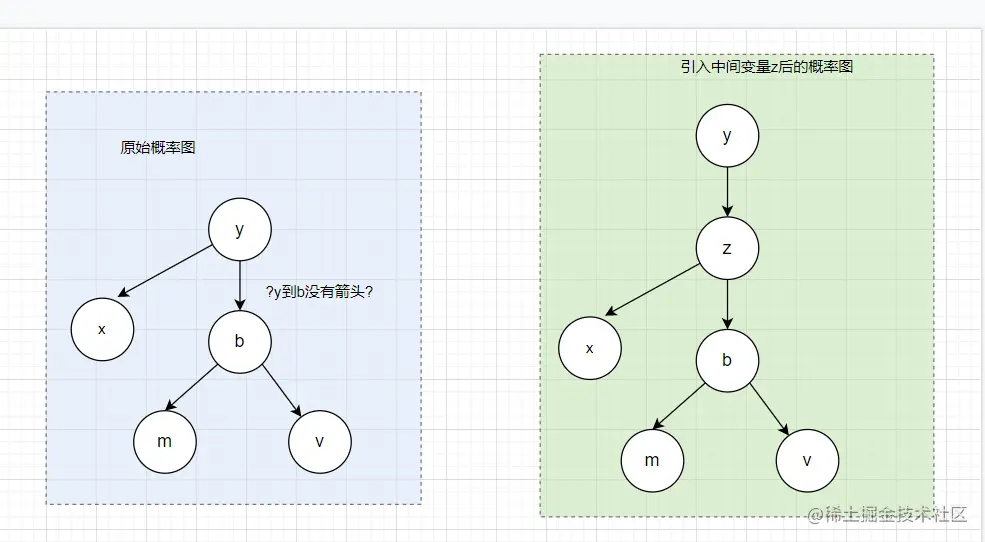
auxiliary variable method (辅助变量法) 继续:

$z=x^T b+\epsilon$ ， 而 $\epsilon \sim \mathcal{N}(0,1)$， 这里的 $x^T$就是$\eta$，得：

$z=\eta+\epsilon$

---

auxiliary variable method (辅助变量法) 继续:

接着 给出y和z之间的关系:

$p(y=1|z,b) = 1 ; 如果 z>0$

$p(y=1|z,b) = 0 ; otherwise$

并且: $p(y=0|z,b)=1-p(y=1|z,b)$

(从概率图上可以看出：z给定时，y与b无关。 所以这个式子中也是这样反映的）

从上式子可以看出:

$p(y=1|z>0,b)=1$， 　　$p(y=1|z \le 0,b)=0$ 　　(p(y=1|z **, b)式子)

---

auxiliary variable method (辅助变量法) 继续:

求 $p(y=1|b)$

$p(y=1|b)=p(y=1|z>0,b) p(z>0|b) +p(y=1|z \le 0, b) p(z \le 0 | b)$，代入 "p(y=1|z **, b)式子" ，得：

$p(y=1|b)=1* p(z>0|b)+0*p(z \le 0 | b)$，即，得：

$p(y=1|b)=p(z>0|b)$

---

废纸箱或垃圾箱：

以下这两个式子是没有下标i的，是张志华老师在[Bayes classifycation] (www.bilibili.com/video/BV1rW…

$p(y|b)={(\mu(b))}^y {(1-\mu(b))}^{(1-y)}$　　：　Bernoulli Distribution (伯努利分布)

$\mu(b)=h(x^T b)$　　

---

需要回答的问题：

为什么要共轭？这个问题估计要继续看完 统计机器学习-张志华 这门课 才有可能有答案

---

统计机器学习-张志华-教学材料

统计机器学习-张志华

---

正确的播放顺序：

4.高斯分布 6.连续分布 5.例子

8.scale mixture pisribarin 7.jeffrey prior 9.statistic interence

40.Markov Chain Monte carlo1 39.Bayesian Classification

(40, 39, 特别是39中的例子， 可以使得把mcmc搞明白)

不用看 "41.Markov Chain Monte carlo2", 因为41和40后半部分一模一样

---

可能会有些用处： 朗道理论物理教程-统计物理学I.pdf

这本书中有一些类似应用题一样的例子，或许可以看看：随机过程（Sheldon M.Ross 著）.pdf

知乎这个人列出来不少统计专业的书籍，或许可以看看： 统计专业书籍推荐

非参数统计 by 陈希孺.pdf 非参数统计 by 陈希孺.pdf zh.u1lib.org

据说有案例？：非参数统计:基于R语言案例分析

机器学习导论-张志华

应用数学基础 张志华

强化学习基础 张志华 实验例子

Deep Learning 中文翻译

张志华 课表

概率分布

GaussionDistribution

Bernoulli Distribution

BernoulliDistribution

练习

试着 将 bayes inference 框架: pyro, 例子 与 理论课 联系起来

试着例子联系理论

例子 理论 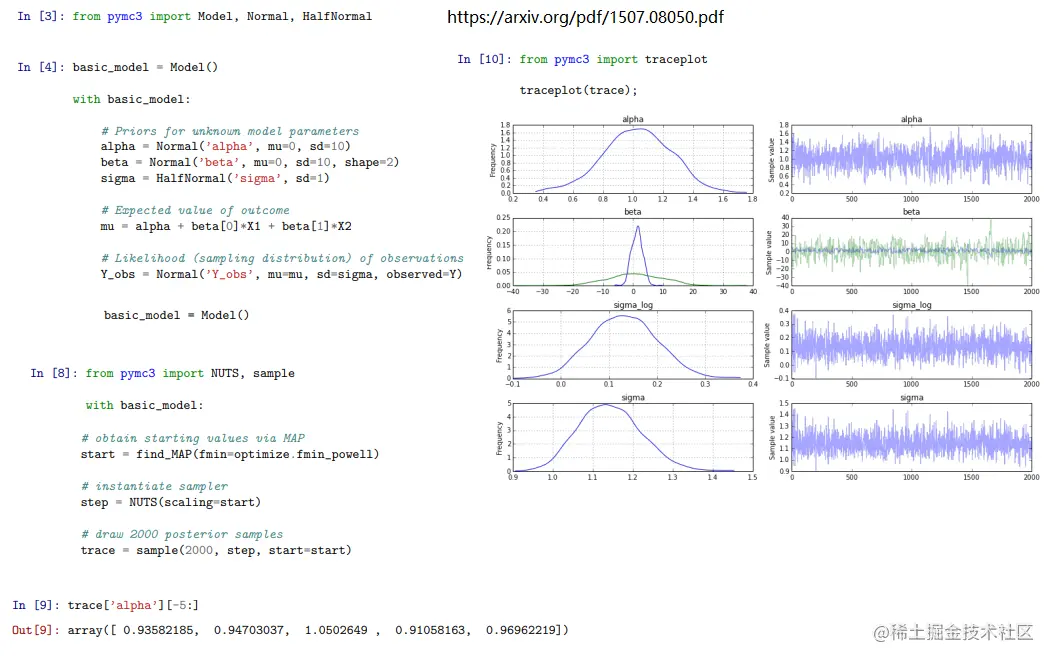例子 联系 理论

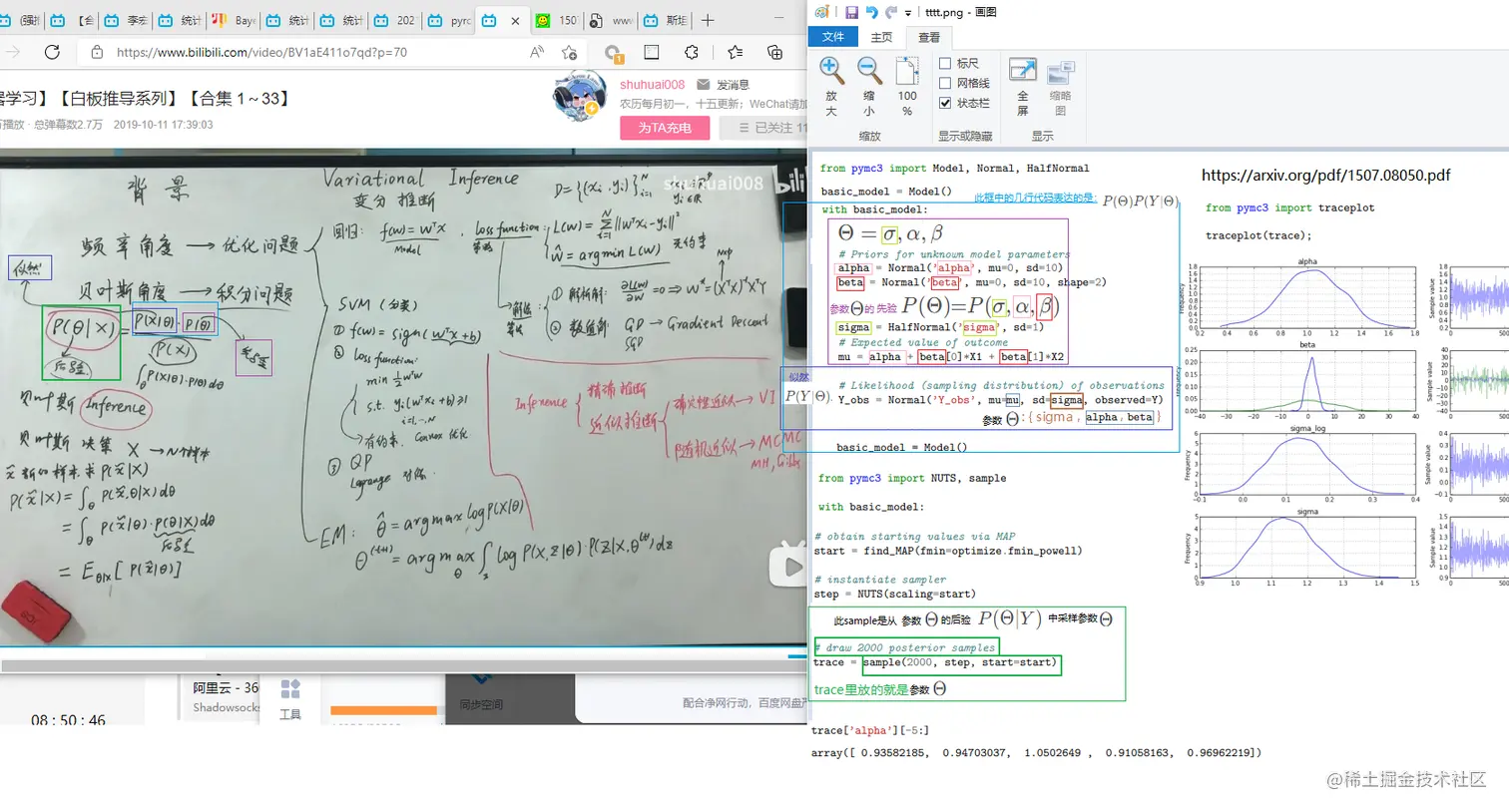
概率图 实例 候选

google search : mcmc github mcmc julia

julia mcmc : Mamba

paperswithcode : variational-inference Gaussian Progress by pytorch :gppytorch

julia mcmc : doobwa/MCMC.jl

mcmc js demo 采样过程ui展示

gibbs sampling python 简单例子 直接是main方法运行

MCMCChains julia: 运行出图?不太确定啥用处

julia turing.ml 09-variational-inference

草稿或垃圾桶

$P(\Theta|Y) = \frac{P(\Theta) P(Y|\Theta) } {P(X)}$

$\Theta=\sigma, \alpha, \beta$

$P(\Theta)=P(\sigma, \alpha, \beta)$

其他资源

西瓜书 李航统计学习方法 实践部分 代码 资料